人教版数学九年级(下册)28.2.1解直角三角形课件(共17张PPT)
文档属性
| 名称 | 人教版数学九年级(下册)28.2.1解直角三角形课件(共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-08 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
人教版九年级下册28章第二节第一课时
角α
三角函数
1
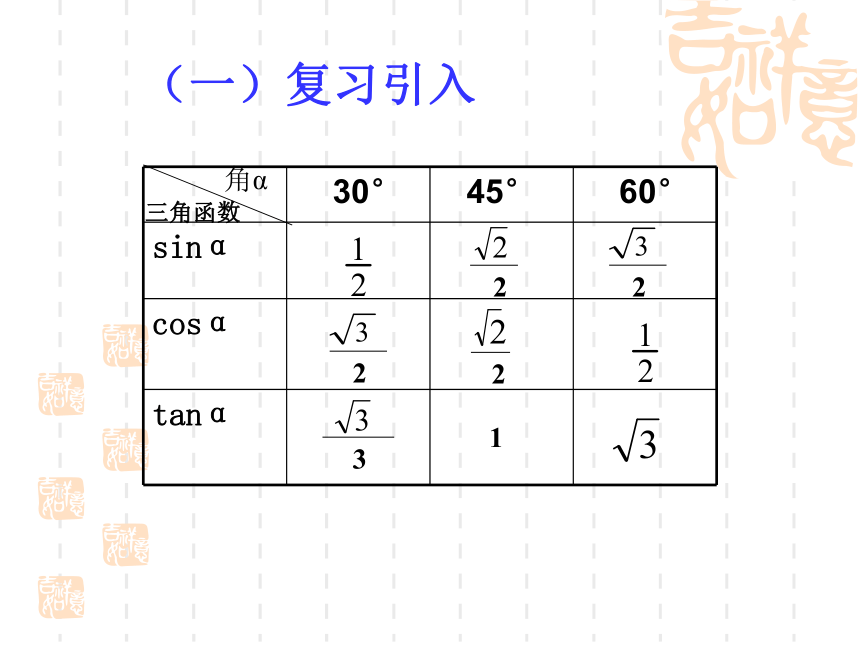
(一)复习引入
30° 45° 60°
sinα
cosα
tanα
1. cos30°=( )
A.
2.计算:-12+6sin60?- +2011°.
3.计算:
考一考
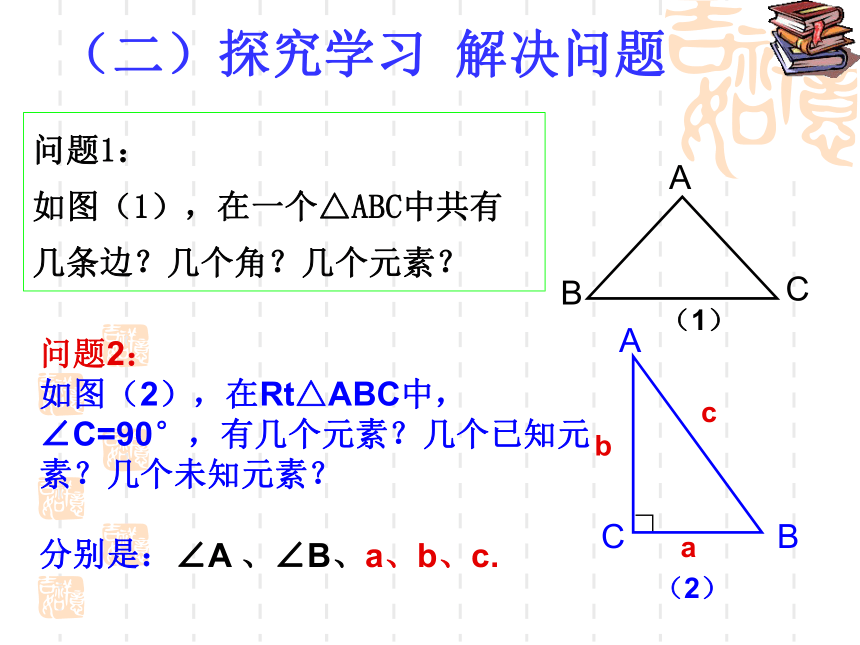
问题1:
如图(1),在一个△ABC中共有几条边?几个角?几个元素?
(二)探究学习 解决问题
问题2:
如图(2),在Rt△ABC中,∠C=90°,有几个元素?几个已知元素?几个未知元素?
分别是:
∟
∠A 、∠B、a、b、c.
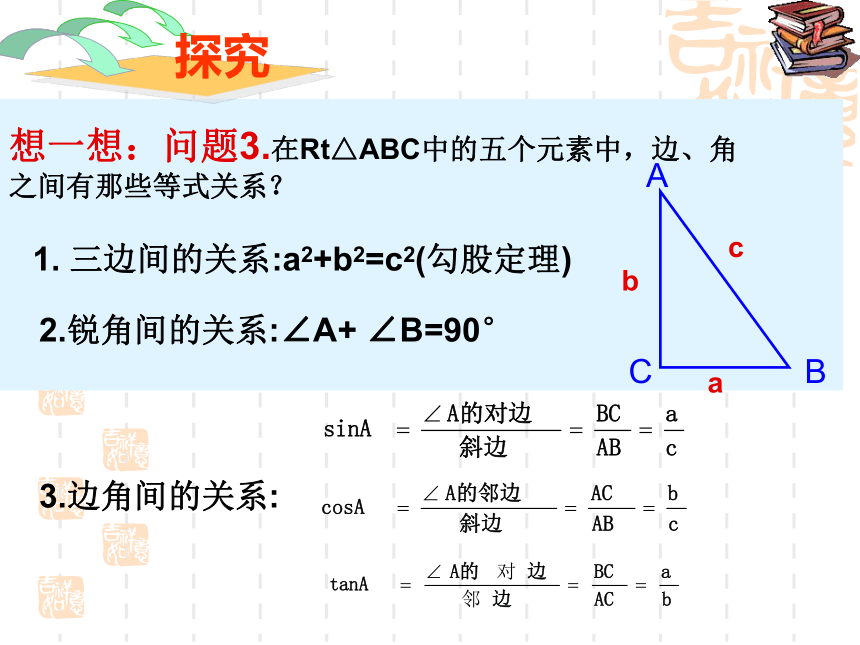
1. 三边间的关系:a2+b2=c2(勾股定理)
2.锐角间的关系:∠A+ ∠B=90°
想一想:问题3.在Rt△ABC中的五个元素中,边、角之间有那些等式关系?
在Rt△ABC中,∠C=90°,a=5, ∠A=30°你能求出这个直角三角形的其他边和角吗?
解:在Rt△ABC中
a=5
c
b
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
解直角三角形:在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
在解直角三角形的过程中,一般要用到下面一些关系:
三.形成概念:解直角三角形
解直角三角形的依据
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90?;
(3)边角之间的关系:
A
B
C
∠A的对边a
∠A的邻边b
斜边c
在直角三角形中,由已知元素求未知元素的过程,叫
(四)自主学习 认识新知
解直角三角形。
A
解:在Rt△ABC中
考一考
在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形
例1.
尽量选择原始数据,避免累积错误
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
在直角三角形的六个元素中,除直角外,如果知道两个元素,
就可以求出其余三个元素.
(其中至少有一个是边),
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?
不能
你能求出这个三角形的其他元素吗?
(五)集体合作 探索规律
1、在下列直角三角形中 不能求解的是( )
A、已知一直角边一锐角
B、已知一斜边一锐角
C、已知两边
D、已知两角
D
考一考
2、在Rt△ABC中,∠C=90度,a,b,c分别是∠A,∠B,∠C的对边.已知 解这个直角三角形
45°
考一考
3. 如图,在△ABC中,∠A=45° , ∠B=30°,BC=8 ,求∠ACB及AC、AB的长。
B
D
解:过C作CD⊥AB于D点。
在Rt △BCD中,∠B=30°,BC=8
∴CD=4.
在Rt △ACD中, ∠A=45 °, ∴AD=CD=4
动动脑
通过这节课的学习,你有什么收获?
www.czsx.com.cn
1.解直角三角形至少要已知两个条件,
其中必须要有一条边,即:
①已知两条边;
②已知一条边和一个角。
必做题:1、课本中1题和2题
2、预习下一节内容
选做作业:
3. 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
作业超市
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.去总结.
结束寄语
人教版九年级下册28章第二节第一课时
角α
三角函数
1
(一)复习引入
30° 45° 60°
sinα
cosα
tanα
1. cos30°=( )
A.
2.计算:-12+6sin60?- +2011°.
3.计算:
考一考
问题1:
如图(1),在一个△ABC中共有几条边?几个角?几个元素?
(二)探究学习 解决问题
问题2:
如图(2),在Rt△ABC中,∠C=90°,有几个元素?几个已知元素?几个未知元素?
分别是:
∟
∠A 、∠B、a、b、c.
1. 三边间的关系:a2+b2=c2(勾股定理)
2.锐角间的关系:∠A+ ∠B=90°
想一想:问题3.在Rt△ABC中的五个元素中,边、角之间有那些等式关系?
在Rt△ABC中,∠C=90°,a=5, ∠A=30°你能求出这个直角三角形的其他边和角吗?
解:在Rt△ABC中
a=5
c
b
事实上,在直角三角形的六个元素中,除直角外,如果再知道两个元素(其中至少有一个是边),这个三角形就可以确定下来,这样就可以由已知的两个元素求出其余的三个元素.
解直角三角形:在直角三角形中,由已知元素求未知元素的过程,叫做解直角三角形.
在解直角三角形的过程中,一般要用到下面一些关系:
三.形成概念:解直角三角形
解直角三角形的依据
(1)三边之间的关系:
a2+b2=c2(勾股定理);
(2)锐角之间的关系:
∠ A+ ∠ B= 90?;
(3)边角之间的关系:
A
B
C
∠A的对边a
∠A的邻边b
斜边c
在直角三角形中,由已知元素求未知元素的过程,叫
(四)自主学习 认识新知
解直角三角形。
A
解:在Rt△ABC中
考一考
在直角三角形中,由已知元素求未知元素的过程,叫解直角三角形
例1.
尽量选择原始数据,避免累积错误
在Rt△ABC中,
(1)根据∠A= 60°,斜边AB=30,
A
在直角三角形的六个元素中,除直角外,如果知道两个元素,
就可以求出其余三个元素.
(其中至少有一个是边),
你发现了什么
B
C
∠B AC BC
∠A ∠B AB
一角一边
两边
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元 素吗?
不能
你能求出这个三角形的其他元素吗?
(五)集体合作 探索规律
1、在下列直角三角形中 不能求解的是( )
A、已知一直角边一锐角
B、已知一斜边一锐角
C、已知两边
D、已知两角
D
考一考
2、在Rt△ABC中,∠C=90度,a,b,c分别是∠A,∠B,∠C的对边.已知 解这个直角三角形
45°
考一考
3. 如图,在△ABC中,∠A=45° , ∠B=30°,BC=8 ,求∠ACB及AC、AB的长。
B
D
解:过C作CD⊥AB于D点。
在Rt △BCD中,∠B=30°,BC=8
∴CD=4.
在Rt △ACD中, ∠A=45 °, ∴AD=CD=4
动动脑
通过这节课的学习,你有什么收获?
www.czsx.com.cn
1.解直角三角形至少要已知两个条件,
其中必须要有一条边,即:
①已知两条边;
②已知一条边和一个角。
必做题:1、课本中1题和2题
2、预习下一节内容
选做作业:
3. 如图,根据图中已知数据,求△ABC其余各边的长,各角的度数和△ABC的面积.
作业超市
悟性的高低取决于有无悟“心”,其实,人与人的差别就在于你是否去思考,去发现.去总结.
结束寄语
