人教版八年级数学上册15.3分式方程(1)课件(共23张)
文档属性
| 名称 | 人教版八年级数学上册15.3分式方程(1)课件(共23张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-08 14:43:05 | ||
图片预览






文档简介
课件23张PPT。15.3 分式方程见课本练习预习检测:学习目标:
1.掌握分式方程的定义.
2.理解解分式方程的一般步骤和分式方程可能产生增根的原因.
3.掌握解分式方程验根的方法。问题引导下的再学习 一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行120千米所用时间,与以最大航速逆流航行80千米所用时间相等,江水的流速为多少?
分析:设江水的流速为x千米/时,填空:
轮船顺流航行速度为___千米/时,逆流航行
速度为___千米/时,顺流航行120千米所用
的时间为___小时,逆流航行80千米所用时间
为___小时。
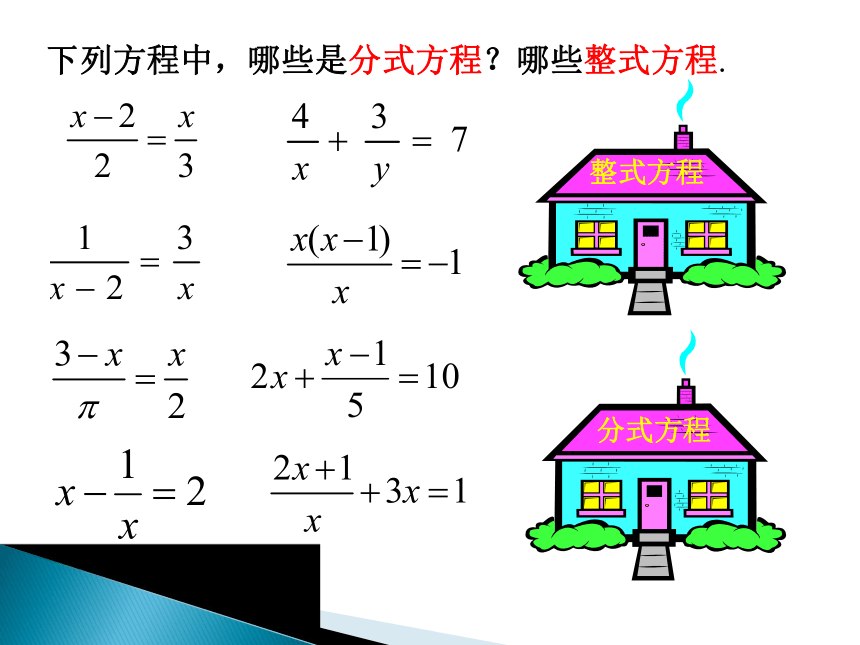
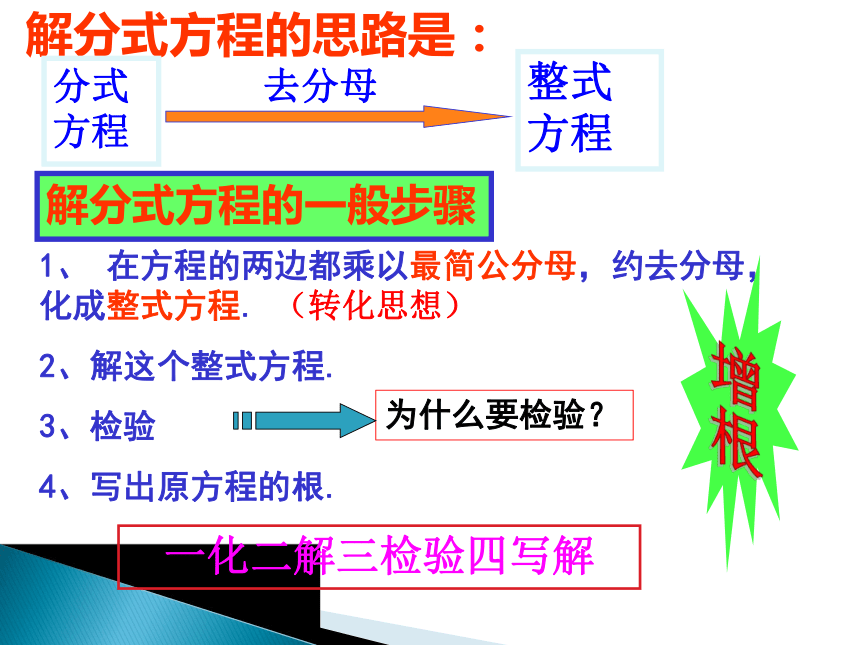
(20+x)(20-x)分式方程像这样,分母里含有未知数的方程叫做分式方程。以前学过的分母里不含有未知数的方程叫做整式方程。 下列方程中,哪些是分式方程?哪些整式方程.解:在方程两边都乘以最简公分母(20+x)(20-x)得,解得x=4120(20-x)=80(20+x)检验:当x= 4 时(20+x)(20-x)≠0因此x=4是原分式方程的解探究下面我们一起研究下怎么样来解分式方程:解分式方程的一般步骤1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程. (转化思想)
2、解这个整式方程.
3、检验
4、写出原方程的根.解分式方程的思路是:分式方程整式方程去分母一化二解三检验四写解为什么要检验?方程两边同乘以最简公分母(x-5)(x+5),得:x+5=10解得:x=5检验:当x=5时最简公分母(x-5)(x+5)=0,所以x=5是增根。原分式方程无解。为什么会产生增根?增根产生的原因?例1:【分式方程的解】思考是原分式方程的解呢?我们来观察去分母的过程120(20-x)=80(20+x)x+5=10两边同乘(20+x)(20-x)当x=4时,(20+x)(20-x)≠0两边同乘(x+5)(x-5)当x=5时, (x+5)(x-5)=0分式两边同乘了不为0的式子,所得整式方程的解与
分式方程的解相同.分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解增根的定义因此解分式方程可能产生增根,解分式方程必须检验怎样检验这个整式方程的解是不是
原分式的解?将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解,否则这个解就不是原分式方程的解.解分式方程(1)(2)当堂训练:(3)达标检测1.m为何值时,方程 会产生增根?k为何值时,方程 无解?思考:“方程有增根”和“方程无解”一样吗?变式1:k为何值时,方程 有解?变式2:练习:“增根”是你可以求出来的,但代入后方
程的分母为0无意义,原方程无解。
“无解”包括增根和这个方程没有可解的根 思考:“方程有增根”和“方程无解”一样吗?小结:1、加深解分式方程的思路2、利用增根解决问题3、分清“有增根”和“无解”的区别 通过例题的讲解和练习的操作,你能总结出解分式方程的一般步骤吗?【小结】解分式方程的一般步骤的框架图:分式方程整式方程a是分式
方程的解X=aa不是分式
方程的解去分母解整式方程检验目标最简公分
母不为0最简公分
母为0谢谢观赏!
1.掌握分式方程的定义.
2.理解解分式方程的一般步骤和分式方程可能产生增根的原因.
3.掌握解分式方程验根的方法。问题引导下的再学习 一艘轮船在静水中的最大航速为20千米/时,它沿江以最大航速顺流航行120千米所用时间,与以最大航速逆流航行80千米所用时间相等,江水的流速为多少?
分析:设江水的流速为x千米/时,填空:
轮船顺流航行速度为___千米/时,逆流航行
速度为___千米/时,顺流航行120千米所用
的时间为___小时,逆流航行80千米所用时间
为___小时。
(20+x)(20-x)分式方程像这样,分母里含有未知数的方程叫做分式方程。以前学过的分母里不含有未知数的方程叫做整式方程。 下列方程中,哪些是分式方程?哪些整式方程.解:在方程两边都乘以最简公分母(20+x)(20-x)得,解得x=4120(20-x)=80(20+x)检验:当x= 4 时(20+x)(20-x)≠0因此x=4是原分式方程的解探究下面我们一起研究下怎么样来解分式方程:解分式方程的一般步骤1、 在方程的两边都乘以最简公分母,约去分母,化成整式方程. (转化思想)
2、解这个整式方程.
3、检验
4、写出原方程的根.解分式方程的思路是:分式方程整式方程去分母一化二解三检验四写解为什么要检验?方程两边同乘以最简公分母(x-5)(x+5),得:x+5=10解得:x=5检验:当x=5时最简公分母(x-5)(x+5)=0,所以x=5是增根。原分式方程无解。为什么会产生增根?增根产生的原因?例1:【分式方程的解】思考是原分式方程的解呢?我们来观察去分母的过程120(20-x)=80(20+x)x+5=10两边同乘(20+x)(20-x)当x=4时,(20+x)(20-x)≠0两边同乘(x+5)(x-5)当x=5时, (x+5)(x-5)=0分式两边同乘了不为0的式子,所得整式方程的解与
分式方程的解相同.分式两边同乘了等于0的式子,所得整式方程的解使分母为0,这个整式方程的解就不是原分式方程的解增根的定义因此解分式方程可能产生增根,解分式方程必须检验怎样检验这个整式方程的解是不是
原分式的解?将整式方程的解代入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解,否则这个解就不是原分式方程的解.解分式方程(1)(2)当堂训练:(3)达标检测1.m为何值时,方程 会产生增根?k为何值时,方程 无解?思考:“方程有增根”和“方程无解”一样吗?变式1:k为何值时,方程 有解?变式2:练习:“增根”是你可以求出来的,但代入后方
程的分母为0无意义,原方程无解。
“无解”包括增根和这个方程没有可解的根 思考:“方程有增根”和“方程无解”一样吗?小结:1、加深解分式方程的思路2、利用增根解决问题3、分清“有增根”和“无解”的区别 通过例题的讲解和练习的操作,你能总结出解分式方程的一般步骤吗?【小结】解分式方程的一般步骤的框架图:分式方程整式方程a是分式
方程的解X=aa不是分式
方程的解去分母解整式方程检验目标最简公分
母不为0最简公分
母为0谢谢观赏!
