人教版八年级数学上册 13.4最短路径问题课件(29张PPT)
文档属性
| 名称 | 人教版八年级数学上册 13.4最短路径问题课件(29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-08 15:29:04 | ||
图片预览




文档简介
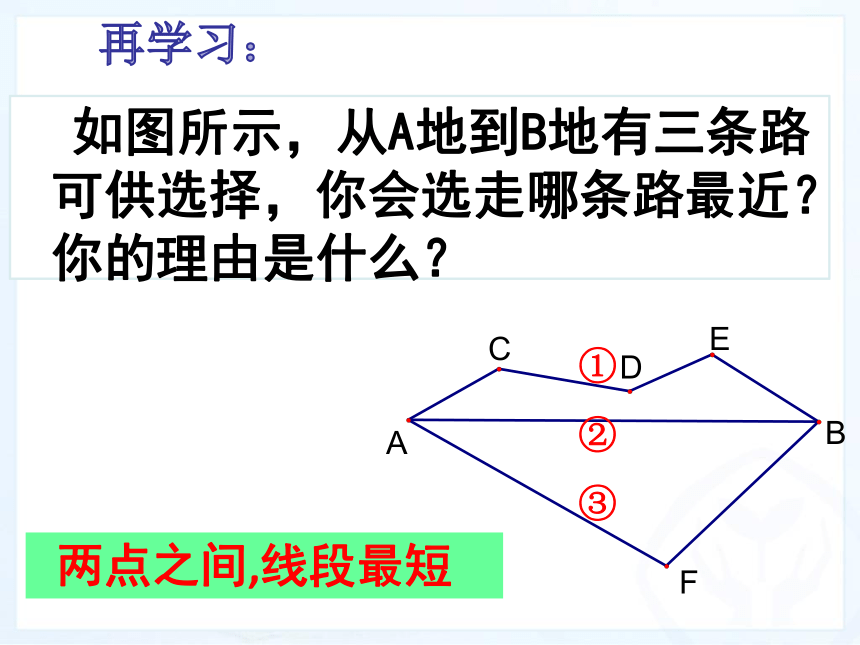
课件29张PPT。八年级 上册13.4 课题学习 最短路径问题预习检测: 如图所示,从A地到B地有三条路可供选择,你会选走哪条路最近?你的理由是什么? 两点之间,线段最短①
②
③再学习: 如图,点A、B分别是直线 l 异侧的两个点,
如何在 l 上找到一个点,使得这个点到点A、点B
的距离的和最短?两点之间,线段最短.l作法:
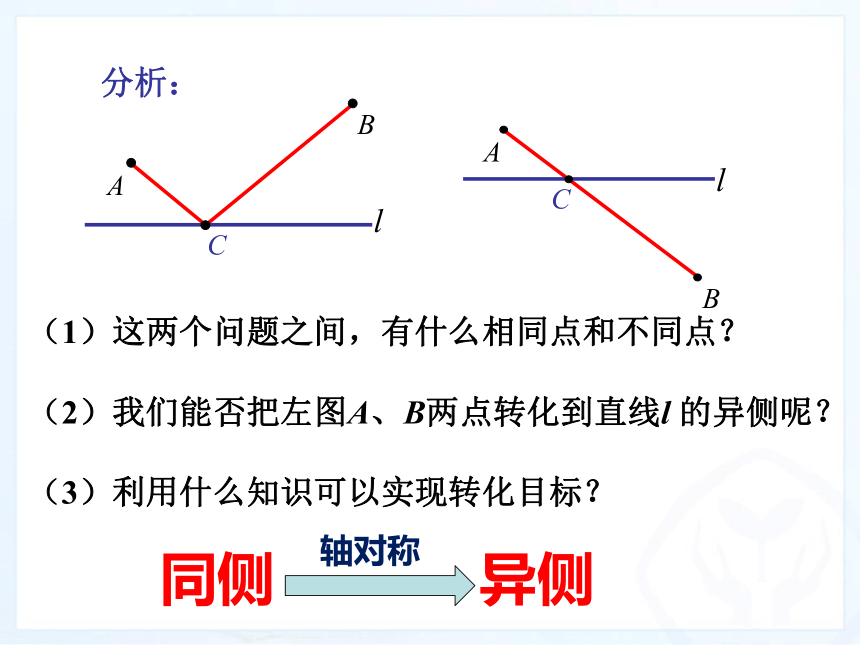
连接两点与直线的交点即为所求的点(1)两点一线:异侧(1)这两个问题之间,有什么相同点和不同点?
(2)我们能否把左图A、B两点转化到直线l 的异侧呢?
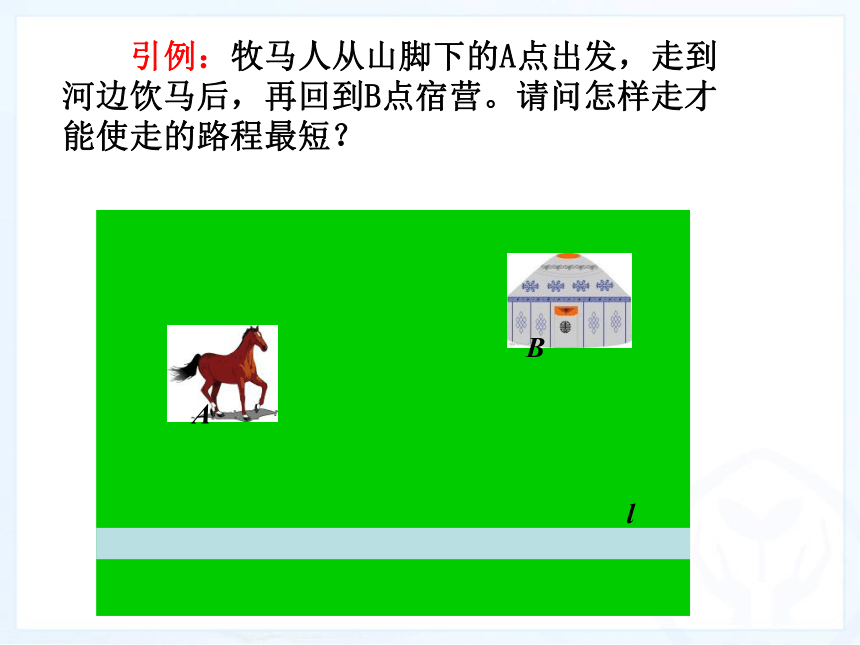
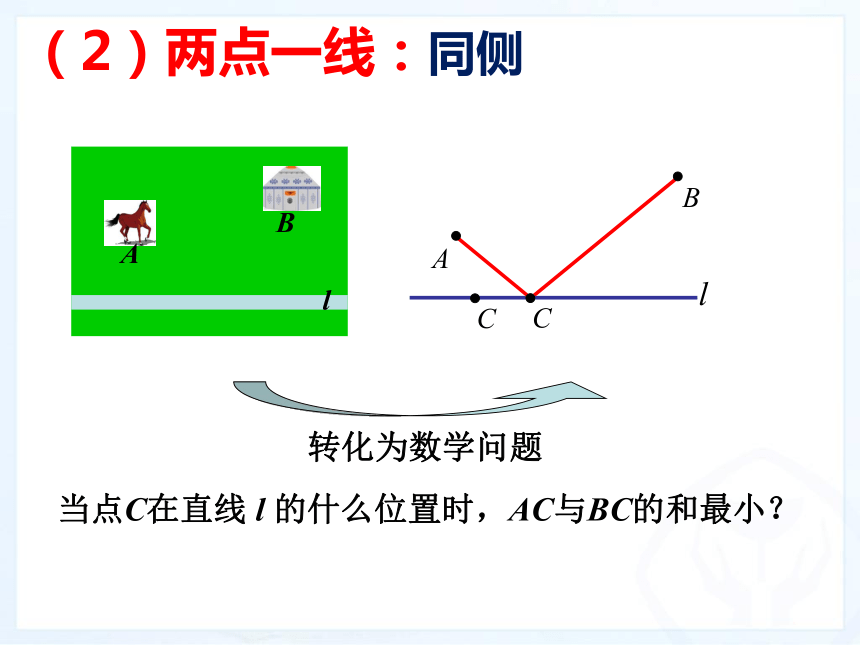
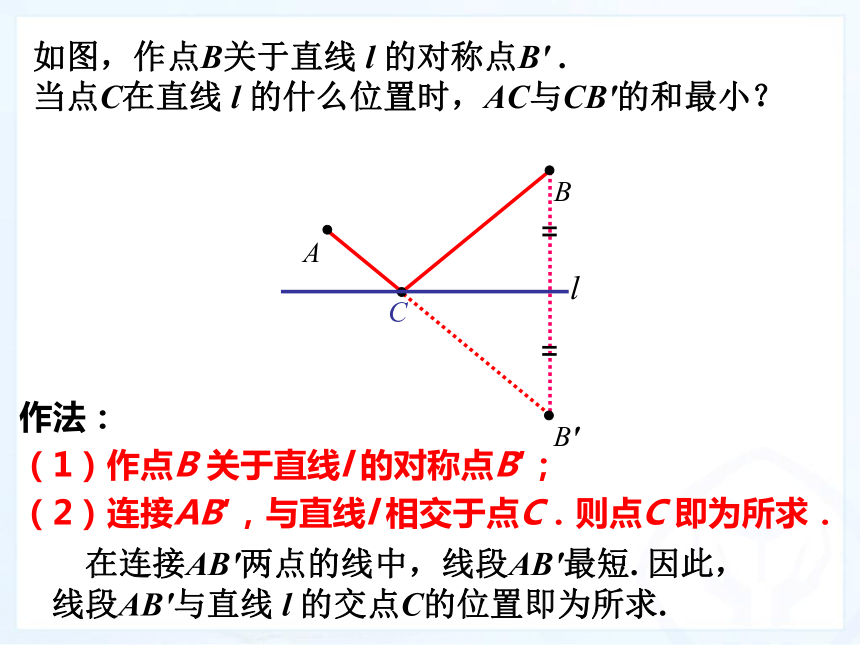
(3)利用什么知识可以实现转化目标?分析:同侧 异侧轴对称 引例:牧马人从山脚下的A点出发,走到河边饮马后,再回到B点宿营。请问怎样走才能使走的路程最短?l当点C在直线 l 的什么位置时,AC与BC的和最小?ABl(2)两点一线:同侧l如图,作点B关于直线 l 的对称点B′ .
当点C在直线 l 的什么位置时,AC与CB′的和最小? 在连接AB′两点的线中,线段AB′最短. 因此,线段AB′与直线 l 的交点C的位置即为所求.作法:
(1)作点B 关于直线l 的对称点B′;
(2)连接AB′,与直线l 相交于点C.则点C 即为所求. 在直线 l 上任取另一点C′ ,
连接AC′ 、BC′ 、B′ C′ .
∵直线 l 是点B、B′的对称轴,
点C、C′在对称轴上,
∴BC=B′C,BC′=B′C′.
∴AC+BC=AC+B′C=AB′.
在△AB′C′中,AB′< AC′+B′C′,
∴AC+BC < AC′+B′C′,
即AC+BC最小.l证明:如图. 归纳解决“两点一线”型最短路径问题的方法:
异侧: 连接两点,与直线的交点即为所求的点;
同侧: 作其中某一点关于直线的对称点,对称点与另一点的连线与直线的交点即为所求的点.1.(中考)如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角D课堂训练: 如图13.4--5,牧马营地在点P处,每天牧马人要赶着马群先到草地a上吃草,再到河边b饮水,最后回到营地.请你设计一条放牧路线,使其所走的总路程最短.2.(3)两线一点图13.4--5ab.p解决“两线一点”型最短路径问题:
要作两次轴对称,从而构造出最短路径.PabP1P2MN.解决“两线一点”型最短路径问题:PabP1P2MN.解决“两线一点”型最短路径问题:
要作两次轴对称,从而构造出最短路径.作法:
1.作点P关于直线a的对称点P1;
2.作点P关于直线b的对称点P2;
3.连接P1P2,分别交直线a ,b于点M ,N ;
4.依次连接PM ,MN ,NP ,即所求最短路径。PabP1P2MN.再学习(4)两线两点.A.B草地河 牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径。l1l2ABA1B1PQ解决“两线两点”型最短路径问题:
1.先作出第一个点A关于直线l1的对称点A1 ;
2.再作出第二个点B关于直线l2的对称点B1 ;
3.连接A1B1,分别交直线l1 , l2于点P , Q ;
4.依次连接AP ,PQ ,QB ,从而构造出最短路径 。..再学习(4)造桥选址问题如图,A和B两地在一条河的两岸,现要在河上造一座桥MN.乔造在何处才能使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)思维分析如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN,那么怎样确定什么情况下最短呢?MN问题解决A1MN如图,平移A到A1,使AA1等于河宽,连接A1B交河岸于N作桥MN,此时路径AM+MN+BN最短.理由;另任作桥M1N1,连接AM1,BN1,A1N1.N1M1由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.AM+MN+BN转化为AA1+A1B,而AM1+M1N1+BN1 转化为AA1+A1N1+BN1.在△A1N1B中,由线段公理知A1N1+BN1>A1B因此AM1+M1N1+BN1 ≥ AM+MN+BN问题2 归纳小结归纳转化轴对称
变换平移
变换两点之间,线段最短.知2-练 1.如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )
A.(-2,0)
B.(4,0)
C.(2,0)
D.(0,0)CB′达标检测:
3.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,求这个最小值。
②
③再学习: 如图,点A、B分别是直线 l 异侧的两个点,
如何在 l 上找到一个点,使得这个点到点A、点B
的距离的和最短?两点之间,线段最短.l作法:
连接两点与直线的交点即为所求的点(1)两点一线:异侧(1)这两个问题之间,有什么相同点和不同点?
(2)我们能否把左图A、B两点转化到直线l 的异侧呢?
(3)利用什么知识可以实现转化目标?分析:同侧 异侧轴对称 引例:牧马人从山脚下的A点出发,走到河边饮马后,再回到B点宿营。请问怎样走才能使走的路程最短?l当点C在直线 l 的什么位置时,AC与BC的和最小?ABl(2)两点一线:同侧l如图,作点B关于直线 l 的对称点B′ .
当点C在直线 l 的什么位置时,AC与CB′的和最小? 在连接AB′两点的线中,线段AB′最短. 因此,线段AB′与直线 l 的交点C的位置即为所求.作法:
(1)作点B 关于直线l 的对称点B′;
(2)连接AB′,与直线l 相交于点C.则点C 即为所求. 在直线 l 上任取另一点C′ ,
连接AC′ 、BC′ 、B′ C′ .
∵直线 l 是点B、B′的对称轴,
点C、C′在对称轴上,
∴BC=B′C,BC′=B′C′.
∴AC+BC=AC+B′C=AB′.
在△AB′C′中,AB′< AC′+B′C′,
∴AC+BC < AC′+B′C′,
即AC+BC最小.l证明:如图. 归纳解决“两点一线”型最短路径问题的方法:
异侧: 连接两点,与直线的交点即为所求的点;
同侧: 作其中某一点关于直线的对称点,对称点与另一点的连线与直线的交点即为所求的点.1.(中考)如图,直线l外不重合的两点A、B,在直线l上求作一点C,使得AC+BC的长度最短,作法为:①作点B关于直线l的对称点B′;②连接AB′与直线l相交于点C,则点C为所求作的点.在解决这个问题时没有运用到的知识或方法是( )
A.转化思想
B.三角形的两边之和大于第三边
C.两点之间,线段最短
D.三角形的一个外角大于与它不相邻的任意一个内角D课堂训练: 如图13.4--5,牧马营地在点P处,每天牧马人要赶着马群先到草地a上吃草,再到河边b饮水,最后回到营地.请你设计一条放牧路线,使其所走的总路程最短.2.(3)两线一点图13.4--5ab.p解决“两线一点”型最短路径问题:
要作两次轴对称,从而构造出最短路径.PabP1P2MN.解决“两线一点”型最短路径问题:PabP1P2MN.解决“两线一点”型最短路径问题:
要作两次轴对称,从而构造出最短路径.作法:
1.作点P关于直线a的对称点P1;
2.作点P关于直线b的对称点P2;
3.连接P1P2,分别交直线a ,b于点M ,N ;
4.依次连接PM ,MN ,NP ,即所求最短路径。PabP1P2MN.再学习(4)两线两点.A.B草地河 牧马人从A地出发,先到草地边某一处牧马,再到河边饮马,然后回到B处,请画出最短路径。l1l2ABA1B1PQ解决“两线两点”型最短路径问题:
1.先作出第一个点A关于直线l1的对称点A1 ;
2.再作出第二个点B关于直线l2的对称点B1 ;
3.连接A1B1,分别交直线l1 , l2于点P , Q ;
4.依次连接AP ,PQ ,QB ,从而构造出最短路径 。..再学习(4)造桥选址问题如图,A和B两地在一条河的两岸,现要在河上造一座桥MN.乔造在何处才能使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)思维分析如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN,那么怎样确定什么情况下最短呢?MN问题解决A1MN如图,平移A到A1,使AA1等于河宽,连接A1B交河岸于N作桥MN,此时路径AM+MN+BN最短.理由;另任作桥M1N1,连接AM1,BN1,A1N1.N1M1由平移性质可知,AM=A1N,AA1=MN=M1N1,AM1=A1N1.AM+MN+BN转化为AA1+A1B,而AM1+M1N1+BN1 转化为AA1+A1N1+BN1.在△A1N1B中,由线段公理知A1N1+BN1>A1B因此AM1+M1N1+BN1 ≥ AM+MN+BN问题2 归纳小结归纳转化轴对称
变换平移
变换两点之间,线段最短.知2-练 1.如图,在平面直角坐标系中,点A(-2,4),B(4,2),在x轴上取一点P,使点P到点A和点B的距离之和最小,则点P的坐标是( )
A.(-2,0)
B.(4,0)
C.(2,0)
D.(0,0)CB′达标检测:
3.如图所示,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,求这个最小值。
