西师大版 六年级上册圆的面积公式应用 教案
文档属性
| 名称 | 西师大版 六年级上册圆的面积公式应用 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 50.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-08 18:08:14 | ||
图片预览




文档简介
圆的周长和面积的应用
教学设计
教学目标
1.进一步练习圆的周长和面积的有关知识。
2.通过实际问题的解决,掌握求组合图形周长或面积的方法,提高思维的灵活性。
3.经历解决问题的过程,学会从不同的角度去分析解决生活中的问题,思考解决问题的不同策略和方案,体会学习圆的知识的现实意义和价值。
教学重点
灵活应用所学知识求组合图形的周长和面积
教学难点
组合图形的周长和面积,解决生活中的实际问题
教学准备
学生练习题单;PPT课件
教学过程
情景引入,基础练习(知识回顾,基础练习6分钟)
同学们,大家好,我是来自自贡23中的江老师,听说我们檀小六()班的同学们非常的聪明,很高兴认识大家。下面老师想和同学们做一个游戏。这个游戏叫“反口令”游戏,你会做吗?游戏规则:老师说动作,你做相反的动作。比如当老师说大西瓜,你们做出小西瓜的手势明白了吗?好,我来试一试。1、请站起来,2、请坐下。
我们六()果然很棒。
1.求绕水池一周的路程,复习圆的周长。( 3 分钟)
师:我们生活中总会遇到一些数学问题。首先请和老师一起来看李爷爷的数学问题。
课件出示问题:在一个晴朗的早晨,李爷爷沿着一个半径是3米的圆形喷水池边散步。李爷爷散步一圈所走的路程是多少?
师:同学们李爷爷散步的喷水池是的形状是?(圆形)沿圆形喷水池走一圈的长度,是圆的什么?
生:周长。(具体感知圆周长的概念。)
师:周长通常用大写字母什么来表示?
生:C。
师:怎样求圆的周长?谁来说一说?
生交流: (板书)已知直径 C=πd
已知半径 C=2πr
师:李爷爷的这个问题里边我们已知了圆的什么?(半径),怎样计算圆的周长?
活动:全班交流。C=2x3.14x3=18.84m。
师:说得真好请坐下,同学们计算的结果和他一样吗?(一样)
2.求小羊最多能吃多少立方米的草,复习圆的面积。( 3 分钟)
我们再来看看小明家的数学问题。
出示问题:小明家有一只小羊,妈妈用一个木桩将羊栓在一片草地上。栓羊的绳子长2米,小羊最多能吃到多少平方米的草?
师:小羊可以怎样活动?(请学生举手说围绕木桩四周一圈活动,最多只能距离木桩2米)会形成一个什么图形?算小羊最多能吃到草的面积,实际上小羊吃草的面积是圆形的什么?
生:面积
师:通常用大写字母什么来表示(S)。
怎样求圆的面积?(让学生对所学的知识和经验进行复习、整理。)谁来说一说。
生:(板书)已知半径 S=πr2。
师:如果已知圆的直径能求出圆的面积吗?那已知周长能算吗?(能,已知直径可以除以二求出半径,再用,,一直周长也可以。。。)
师:在求圆的面积时,不论已知什么条件,都要先求出圆的半径,再利用半径就能算出圆的面积。
师:这个问题里,栓羊的绳长实际上是圆的什么?
生:圆的半径,就是2米
师:你能求出圆的面积了吗?口算行吗?
活动:生口算圆的面积,(举手) S=3.14x22=12.56m2。
师:说得真好请坐下,同学们计算的结果和他一样吗?
深化练习(20分钟)
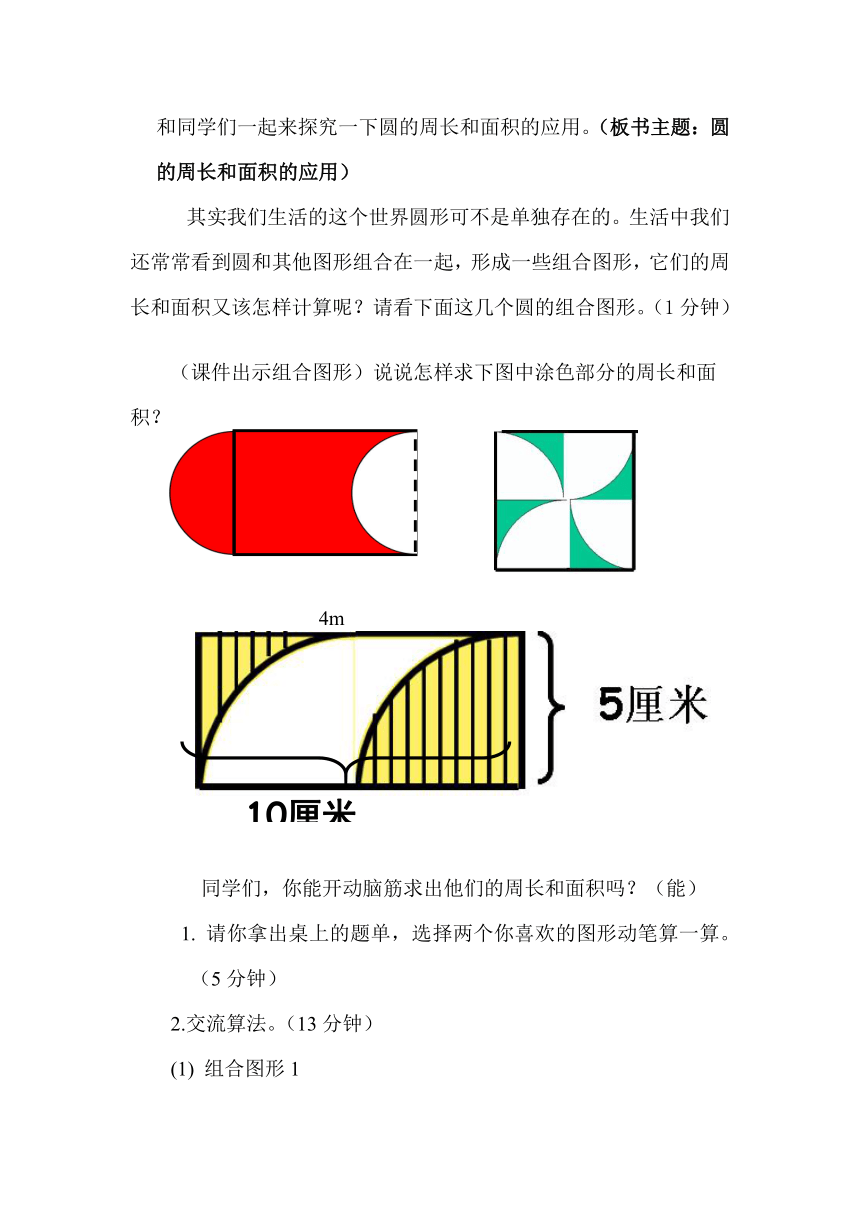
看来,生活中经常要运用圆的周长和面积的知识。今天,老师就和同学们一起来探究一下圆的周长和面积的应用。(板书主题:圆的周长和面积的应用)
其实我们生活的这个世界圆形可不是单独存在的。生活中我们还常常看到圆和其他图形组合在一起,形成一些组合图形,它们的周长和面积又该怎样计算呢?请看下面这几个圆的组合图形。(1分钟)
(课件出示组合图形)说说怎样求下图中涂色部分的周长和面积?
5m 2dm
4m
同学们,你能开动脑筋求出他们的周长和面积吗?(能)
1. 请你拿出桌上的题单,选择两个你喜欢的图形动笔算一算。(5分钟)
2.交流算法。(13分钟)
(1) 组合图形1
师:选择第一个图形的同学请举手。
师:计算组合图形涂色部分的周长,首先要确定它的周长和面积是由哪几部分组成的,谁来指一指。
生:指(师引导,这是什么一段曲线?左边一个半圆弧,右边也是一个半圆弧,上面和下各是5米的线段。)
师:同学们同意他的说法吗?(同意)红色部分的周长包括左边一个半圆弧,右边也是一个半圆弧,上面和下各是5米的线段。)
师:谁想在投影仪上展示一下你的做法,在展示的过程中,请你说说你是怎么想的,因为老师更想知道你的想法。
生1: 我想的是这个图形的周长包括两个半圆弧,合起来就是一个圆的周长,再加上下两条长方形的长。
C=5*2+4π=10+12.56=22.56(米)
师:5*2算的是什么? 4π呢?
师:求组合图形的周长时首先要认真观察阴影部分的周长是由哪几部分组成的,最后确定解答方法。
师:面积
生1:S=5*4=20(平方米)
师:5x4算的是什么,(长方形的面积),也就是说长方形的面积和红色部分的面积是(相等的)你是怎么知道的?
生:我是将左边的半圆平移右边到空白半圆处,原来的图形就被转化成一个长方形。所以阴影部分的面积就等于长方形的面积。
师:将左边的半圆平移右边到空白半圆处,原来的图形就被转化成一个长方形。长方形的面积就是涂色部分的面积。
师:同学们觉得他的办法怎么样?(很好)好在哪里?(计算起来很简单)
还有没有别的算法?
若有,请学生比较哪种算法更简单。
师小结:对,通过平移的办法,将图形转化为基本图形进行,这样会让计算更简便。
(2)组合图形2:
师:选择第二个图形进行计算的同学请举手。
这个组合图形的周长和面积怎样计算的呢?哪位同学想来展示一下你的做法?同样的请你在展示的同时,说一说你的想法。
生1:我经过观察可以把这个组合图形的四个部分旋转一下,把空白部分都旋转到以正方形的中心为圆心,这样,这个图形的周长外面就是整个正方形的周长,里面是圆的周长。
所以 C=4 X 2+πx2
=8+2X3.14
=8+6.28
=14.28(分米)
生2:阴影部分的是四个相同的形状组成,因此,我们,只需算出一个图形的周长,就可以算出4个的周长了。
C=(2+ *2*1*π)*4
=8+2π
=8+6.28
=14.28分米
生3:绿色部分的是由四个一样的图形组成的,只是位置不同而已,因此,周长应该是4个四分之一圆的周长,再加上8条二分之一正方形的边长,也就是四条正方形的边长,实际上就是正方形的周长。
因此C=4*( *2*1*π)+2* *8
=2π+8
=6.28+8
=14.28分米
师: 这里再一次告诉我们算阴影不部分的周长,首先一定要仔细观察阴影部分的周长是有哪几部分组成的。
刚才我们几位同学都说了不同周长的求法,那么绿色部分的面积又该怎样求呢?哪位同学来说一下你的看法?
生1:我是这样想的,整个图形是一个边长为2分米的正方形,而四个空白部分组合起来是一个半径是1分米的圆,所以,阴影部分的面积就可以用(正方形的面积-圆的面积)
我是用大正方形的面积,减去半径是1分米的圆的面积
S =22-—π*12
=4—3.14
=0.86(平方分米)
师:2的平方算的是什么?π*12 算的什么?你怎么知道阴影部分的面积就等于大正方形的面积减圆的面积的呢?
生:我是通过旋转,将空白部分转到中间,合起来就是一个圆形。
圆的半径是1分米。
生2:阴影部分是4个相同的形状,我们只要算出一个的面积就可以算出四个的面积,
S = (12 - *π*12) *4
=(1—0.785)*4
=0.215*4
=0.86(平方分米)
师:刚才几位同学的算法,你认为那种最简单呢?
生:
师:对,通过旋转,能将复杂的图形转化为简单的基本图形,起到化繁为简的效果。
师小结:所以我们在做题的时候,应该仔细观察图形,通过旋转的办法,将图形转化为基本图形,这样会让计算更简便。化零为整。此外有时还要综合运用,才能透过复杂现象,寻求到解决问题的办法。
活动:眼力大比拼
师:三个正方形中阴影面积相等吗?为什么
生:相等,因为三个图形中的空白部分的都可以转化成一个面积相等的圆。
师:有补充的吗?(谁能)
(3) 组合图形3
情形(1) 师:请选第三个图形的请举手,有难度吗?先让我们来仔细观察一下这个图形, 如果老师这里帮你画出一条分割线,请你再仔细观察一下,你有什么发现?
师:请一个同学来指一指它的周长包括哪些部分。
怎样计算:5x4+3.14x5=20+15.70=35.70(厘米)
生1:这个黄色部分被分成了一个四分之一圆和剩余部分,剩余部分的面积就是边长5厘米的正方形的面积减去一个四分之一圆
S(=52 -- xπx 52)+ πx52
=25(平方厘米)
生2:分割线将长方形分成了两个正方形,阴影部分也被分成了两块,左边的阴影刚好可以补上右边正方形的空白,这样实际上阴影部分的面积就是一个正方形的面积,边长是5厘米,
所以 S=52=25(平方厘米)
师:这位同学用的是什么办法来算这个组合图形的面积呢?
生:割补法
师:他们两位同学的算法那种更简便?
师:通过分割填补的办法,可以将这个阴影部分的面积转换成正方形。这样计算就简便多了。
3.师小结(2分钟)
六年级()班的同学们真的很棒,一会儿的功夫就把这三个圆的组合图形的周长和面积。我们现在一起来总结一下,在计算这几组合图形的周长和面积时,我们用到了什么好的方法?
师: 像这样求组合图形涂色部分的周长和面积时,先要仔细观察,通过平移,旋转,分割填补的方法,将其转化为简单的基本图形,根据已知条件分别求出基本图形的面积,再求出基本图形面积之和或面积之差,就可以求得涂色部分面积。
拓展练习(8分钟)
课件出示问题(一):.一只小狗被主人栓在屋外的一面墙上,墙的长度是6米,栓狗绳的长是3米。
(1)小狗的最大活动是多大?
(2)尝试多种栓法,狗的活动范围是否都一样?
(3)如果不一样,哪种栓法,小狗的活动范围最大,是多大?
[ 师:下面我们来看一个拓展练习,读题,让学生弄懂提议。
请同学们分组讨论。必要的时候可以在图上画一画。]
分组讨论(3分钟)
师:同学们都讨论好了吗?哪一组的同学来说一说你们的看法。第一个问题,小狗的最大活动有多大?
交流算法:(5分钟)
组1:我们组认为,小狗的活动范围是半径为3米的半圆,是哪个半圆,请你来指一指。所以它的活动范围是S=3.14x32x =14.13(平方米)
师:其他组和他们的看法一样吗?(一样)
师:第二个问题:尝试不同的栓法,小狗的活动范围都一样吗?哪个组的同学来说一说?
组2:我们认为不同的栓法,小狗的活动范围是不一样的。(师:为什么?)
如果栓在墙角处它的活动范围就更大了,是四分之三圆的面积。其他组的意见一致吗?很好请坐。
师:第三个问题那种栓狗的活动范围最大?是多大?
哪个组的同学来说一说?
组3:栓在墙角处的活动范围师最大的,
S= S=3.14x32x = (平方米)
思考题(机动题)
师:下面请看一个思考题。(生齐读题,弄清提议,师出示 示意图)
请同学们独立思考解决。
这个题,就留给同学们下来思考解决。
四、课堂小结(2分钟)
通过今天的学习,你学到了什么知识?你有哪些收获?求组合图形的阴影面积时一般会遇到什么情况?有什么宝贵的解题经验想和大家分享?
谁来说一说?
生:
师:我们经常会遇到一些,看起来较复杂的组合图形,求他们的周长是时,我们首先要看看清楚它的周长是有哪些部分组成,再选择合适的方法进行计算。而在算组合的图形的面积时,我们要仔细观察组合图形各部分之间的关系,再利用平移,旋转,割补的办法,将复杂图形转化为简单的基本图形,这样就会将问题简单化,方便我们计算。
同学们,这节课就上到这里,再见。
五、板书设计
圆的周长和面积的应用
周长 C 面积S
已知直径:C=πd 已知半径:S=πr2。
已知半径 C=2πr
平移 旋转 分割
组合图形------ ---- -------- ---- 基本图形
转化
教学设计
教学目标
1.进一步练习圆的周长和面积的有关知识。
2.通过实际问题的解决,掌握求组合图形周长或面积的方法,提高思维的灵活性。
3.经历解决问题的过程,学会从不同的角度去分析解决生活中的问题,思考解决问题的不同策略和方案,体会学习圆的知识的现实意义和价值。
教学重点
灵活应用所学知识求组合图形的周长和面积
教学难点
组合图形的周长和面积,解决生活中的实际问题
教学准备
学生练习题单;PPT课件
教学过程
情景引入,基础练习(知识回顾,基础练习6分钟)
同学们,大家好,我是来自自贡23中的江老师,听说我们檀小六()班的同学们非常的聪明,很高兴认识大家。下面老师想和同学们做一个游戏。这个游戏叫“反口令”游戏,你会做吗?游戏规则:老师说动作,你做相反的动作。比如当老师说大西瓜,你们做出小西瓜的手势明白了吗?好,我来试一试。1、请站起来,2、请坐下。
我们六()果然很棒。
1.求绕水池一周的路程,复习圆的周长。( 3 分钟)
师:我们生活中总会遇到一些数学问题。首先请和老师一起来看李爷爷的数学问题。
课件出示问题:在一个晴朗的早晨,李爷爷沿着一个半径是3米的圆形喷水池边散步。李爷爷散步一圈所走的路程是多少?
师:同学们李爷爷散步的喷水池是的形状是?(圆形)沿圆形喷水池走一圈的长度,是圆的什么?
生:周长。(具体感知圆周长的概念。)
师:周长通常用大写字母什么来表示?
生:C。
师:怎样求圆的周长?谁来说一说?
生交流: (板书)已知直径 C=πd
已知半径 C=2πr
师:李爷爷的这个问题里边我们已知了圆的什么?(半径),怎样计算圆的周长?
活动:全班交流。C=2x3.14x3=18.84m。
师:说得真好请坐下,同学们计算的结果和他一样吗?(一样)
2.求小羊最多能吃多少立方米的草,复习圆的面积。( 3 分钟)
我们再来看看小明家的数学问题。
出示问题:小明家有一只小羊,妈妈用一个木桩将羊栓在一片草地上。栓羊的绳子长2米,小羊最多能吃到多少平方米的草?
师:小羊可以怎样活动?(请学生举手说围绕木桩四周一圈活动,最多只能距离木桩2米)会形成一个什么图形?算小羊最多能吃到草的面积,实际上小羊吃草的面积是圆形的什么?
生:面积
师:通常用大写字母什么来表示(S)。
怎样求圆的面积?(让学生对所学的知识和经验进行复习、整理。)谁来说一说。
生:(板书)已知半径 S=πr2。
师:如果已知圆的直径能求出圆的面积吗?那已知周长能算吗?(能,已知直径可以除以二求出半径,再用,,一直周长也可以。。。)
师:在求圆的面积时,不论已知什么条件,都要先求出圆的半径,再利用半径就能算出圆的面积。
师:这个问题里,栓羊的绳长实际上是圆的什么?
生:圆的半径,就是2米
师:你能求出圆的面积了吗?口算行吗?
活动:生口算圆的面积,(举手) S=3.14x22=12.56m2。
师:说得真好请坐下,同学们计算的结果和他一样吗?
深化练习(20分钟)
看来,生活中经常要运用圆的周长和面积的知识。今天,老师就和同学们一起来探究一下圆的周长和面积的应用。(板书主题:圆的周长和面积的应用)
其实我们生活的这个世界圆形可不是单独存在的。生活中我们还常常看到圆和其他图形组合在一起,形成一些组合图形,它们的周长和面积又该怎样计算呢?请看下面这几个圆的组合图形。(1分钟)
(课件出示组合图形)说说怎样求下图中涂色部分的周长和面积?
5m 2dm
4m
同学们,你能开动脑筋求出他们的周长和面积吗?(能)
1. 请你拿出桌上的题单,选择两个你喜欢的图形动笔算一算。(5分钟)
2.交流算法。(13分钟)
(1) 组合图形1
师:选择第一个图形的同学请举手。
师:计算组合图形涂色部分的周长,首先要确定它的周长和面积是由哪几部分组成的,谁来指一指。
生:指(师引导,这是什么一段曲线?左边一个半圆弧,右边也是一个半圆弧,上面和下各是5米的线段。)
师:同学们同意他的说法吗?(同意)红色部分的周长包括左边一个半圆弧,右边也是一个半圆弧,上面和下各是5米的线段。)
师:谁想在投影仪上展示一下你的做法,在展示的过程中,请你说说你是怎么想的,因为老师更想知道你的想法。
生1: 我想的是这个图形的周长包括两个半圆弧,合起来就是一个圆的周长,再加上下两条长方形的长。
C=5*2+4π=10+12.56=22.56(米)
师:5*2算的是什么? 4π呢?
师:求组合图形的周长时首先要认真观察阴影部分的周长是由哪几部分组成的,最后确定解答方法。
师:面积
生1:S=5*4=20(平方米)
师:5x4算的是什么,(长方形的面积),也就是说长方形的面积和红色部分的面积是(相等的)你是怎么知道的?
生:我是将左边的半圆平移右边到空白半圆处,原来的图形就被转化成一个长方形。所以阴影部分的面积就等于长方形的面积。
师:将左边的半圆平移右边到空白半圆处,原来的图形就被转化成一个长方形。长方形的面积就是涂色部分的面积。
师:同学们觉得他的办法怎么样?(很好)好在哪里?(计算起来很简单)
还有没有别的算法?
若有,请学生比较哪种算法更简单。
师小结:对,通过平移的办法,将图形转化为基本图形进行,这样会让计算更简便。
(2)组合图形2:
师:选择第二个图形进行计算的同学请举手。
这个组合图形的周长和面积怎样计算的呢?哪位同学想来展示一下你的做法?同样的请你在展示的同时,说一说你的想法。
生1:我经过观察可以把这个组合图形的四个部分旋转一下,把空白部分都旋转到以正方形的中心为圆心,这样,这个图形的周长外面就是整个正方形的周长,里面是圆的周长。
所以 C=4 X 2+πx2
=8+2X3.14
=8+6.28
=14.28(分米)
生2:阴影部分的是四个相同的形状组成,因此,我们,只需算出一个图形的周长,就可以算出4个的周长了。
C=(2+ *2*1*π)*4
=8+2π
=8+6.28
=14.28分米
生3:绿色部分的是由四个一样的图形组成的,只是位置不同而已,因此,周长应该是4个四分之一圆的周长,再加上8条二分之一正方形的边长,也就是四条正方形的边长,实际上就是正方形的周长。
因此C=4*( *2*1*π)+2* *8
=2π+8
=6.28+8
=14.28分米
师: 这里再一次告诉我们算阴影不部分的周长,首先一定要仔细观察阴影部分的周长是有哪几部分组成的。
刚才我们几位同学都说了不同周长的求法,那么绿色部分的面积又该怎样求呢?哪位同学来说一下你的看法?
生1:我是这样想的,整个图形是一个边长为2分米的正方形,而四个空白部分组合起来是一个半径是1分米的圆,所以,阴影部分的面积就可以用(正方形的面积-圆的面积)
我是用大正方形的面积,减去半径是1分米的圆的面积
S =22-—π*12
=4—3.14
=0.86(平方分米)
师:2的平方算的是什么?π*12 算的什么?你怎么知道阴影部分的面积就等于大正方形的面积减圆的面积的呢?
生:我是通过旋转,将空白部分转到中间,合起来就是一个圆形。
圆的半径是1分米。
生2:阴影部分是4个相同的形状,我们只要算出一个的面积就可以算出四个的面积,
S = (12 - *π*12) *4
=(1—0.785)*4
=0.215*4
=0.86(平方分米)
师:刚才几位同学的算法,你认为那种最简单呢?
生:
师:对,通过旋转,能将复杂的图形转化为简单的基本图形,起到化繁为简的效果。
师小结:所以我们在做题的时候,应该仔细观察图形,通过旋转的办法,将图形转化为基本图形,这样会让计算更简便。化零为整。此外有时还要综合运用,才能透过复杂现象,寻求到解决问题的办法。
活动:眼力大比拼
师:三个正方形中阴影面积相等吗?为什么
生:相等,因为三个图形中的空白部分的都可以转化成一个面积相等的圆。
师:有补充的吗?(谁能)
(3) 组合图形3
情形(1) 师:请选第三个图形的请举手,有难度吗?先让我们来仔细观察一下这个图形, 如果老师这里帮你画出一条分割线,请你再仔细观察一下,你有什么发现?
师:请一个同学来指一指它的周长包括哪些部分。
怎样计算:5x4+3.14x5=20+15.70=35.70(厘米)
生1:这个黄色部分被分成了一个四分之一圆和剩余部分,剩余部分的面积就是边长5厘米的正方形的面积减去一个四分之一圆
S(=52 -- xπx 52)+ πx52
=25(平方厘米)
生2:分割线将长方形分成了两个正方形,阴影部分也被分成了两块,左边的阴影刚好可以补上右边正方形的空白,这样实际上阴影部分的面积就是一个正方形的面积,边长是5厘米,
所以 S=52=25(平方厘米)
师:这位同学用的是什么办法来算这个组合图形的面积呢?
生:割补法
师:他们两位同学的算法那种更简便?
师:通过分割填补的办法,可以将这个阴影部分的面积转换成正方形。这样计算就简便多了。
3.师小结(2分钟)
六年级()班的同学们真的很棒,一会儿的功夫就把这三个圆的组合图形的周长和面积。我们现在一起来总结一下,在计算这几组合图形的周长和面积时,我们用到了什么好的方法?
师: 像这样求组合图形涂色部分的周长和面积时,先要仔细观察,通过平移,旋转,分割填补的方法,将其转化为简单的基本图形,根据已知条件分别求出基本图形的面积,再求出基本图形面积之和或面积之差,就可以求得涂色部分面积。
拓展练习(8分钟)
课件出示问题(一):.一只小狗被主人栓在屋外的一面墙上,墙的长度是6米,栓狗绳的长是3米。
(1)小狗的最大活动是多大?
(2)尝试多种栓法,狗的活动范围是否都一样?
(3)如果不一样,哪种栓法,小狗的活动范围最大,是多大?
[ 师:下面我们来看一个拓展练习,读题,让学生弄懂提议。
请同学们分组讨论。必要的时候可以在图上画一画。]
分组讨论(3分钟)
师:同学们都讨论好了吗?哪一组的同学来说一说你们的看法。第一个问题,小狗的最大活动有多大?
交流算法:(5分钟)
组1:我们组认为,小狗的活动范围是半径为3米的半圆,是哪个半圆,请你来指一指。所以它的活动范围是S=3.14x32x =14.13(平方米)
师:其他组和他们的看法一样吗?(一样)
师:第二个问题:尝试不同的栓法,小狗的活动范围都一样吗?哪个组的同学来说一说?
组2:我们认为不同的栓法,小狗的活动范围是不一样的。(师:为什么?)
如果栓在墙角处它的活动范围就更大了,是四分之三圆的面积。其他组的意见一致吗?很好请坐。
师:第三个问题那种栓狗的活动范围最大?是多大?
哪个组的同学来说一说?
组3:栓在墙角处的活动范围师最大的,
S= S=3.14x32x = (平方米)
思考题(机动题)
师:下面请看一个思考题。(生齐读题,弄清提议,师出示 示意图)
请同学们独立思考解决。
这个题,就留给同学们下来思考解决。
四、课堂小结(2分钟)
通过今天的学习,你学到了什么知识?你有哪些收获?求组合图形的阴影面积时一般会遇到什么情况?有什么宝贵的解题经验想和大家分享?
谁来说一说?
生:
师:我们经常会遇到一些,看起来较复杂的组合图形,求他们的周长是时,我们首先要看看清楚它的周长是有哪些部分组成,再选择合适的方法进行计算。而在算组合的图形的面积时,我们要仔细观察组合图形各部分之间的关系,再利用平移,旋转,割补的办法,将复杂图形转化为简单的基本图形,这样就会将问题简单化,方便我们计算。
同学们,这节课就上到这里,再见。
五、板书设计
圆的周长和面积的应用
周长 C 面积S
已知直径:C=πd 已知半径:S=πr2。
已知半径 C=2πr
平移 旋转 分割
组合图形------ ---- -------- ---- 基本图形
转化
