冀教版2019秋八年级数学下册22.5菱形第2课时菱形的判定教学课件(30张ppt)
文档属性
| 名称 | 冀教版2019秋八年级数学下册22.5菱形第2课时菱形的判定教学课件(30张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 263.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 15:05:31 | ||
图片预览





文档简介
课件30张PPT。导入新课讲授新课当堂练习课堂小结22.5 菱形第二十二章 四边形第2课时 菱形的判定 1.经历菱形判定定理的探究过程,掌握菱形的判
定定理.(重点)
2.会用这些菱形的判定方法进行有关的证明和计算.
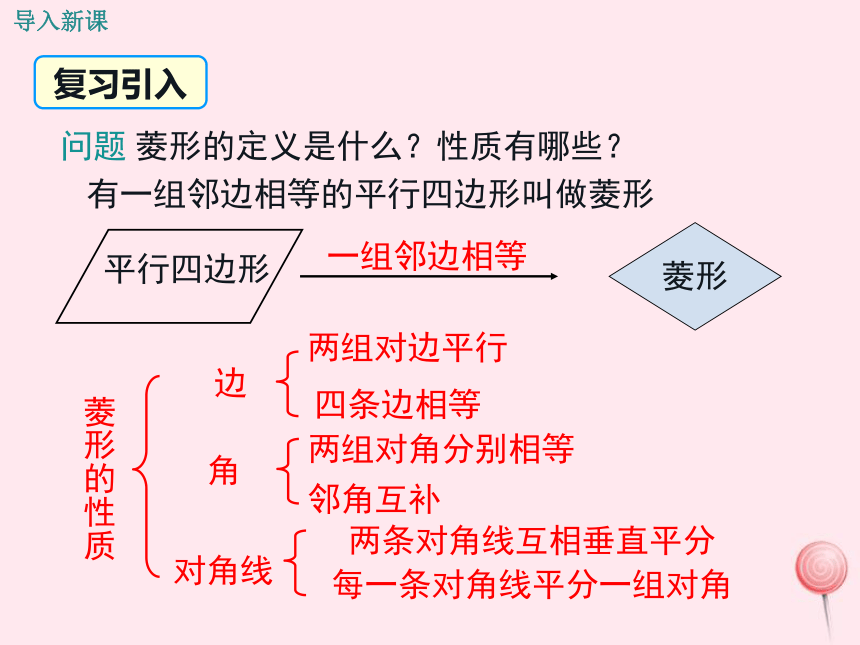
(难点)一组邻边相等有一组邻边相等的平行四边形叫做菱形菱形的性质菱形两组对边平行四条边相等两组对角分别相等 邻角互补两条对角线互相垂直平分
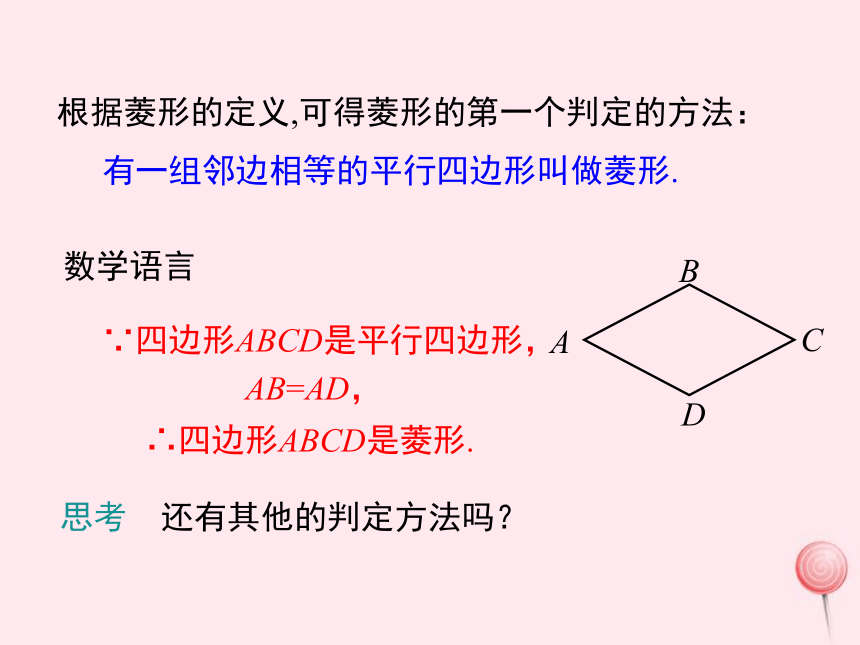
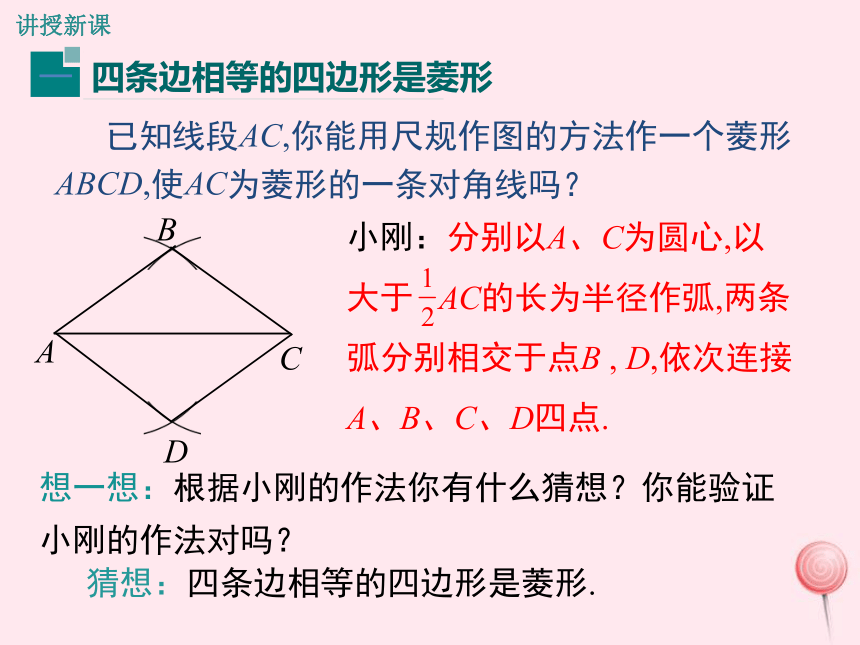
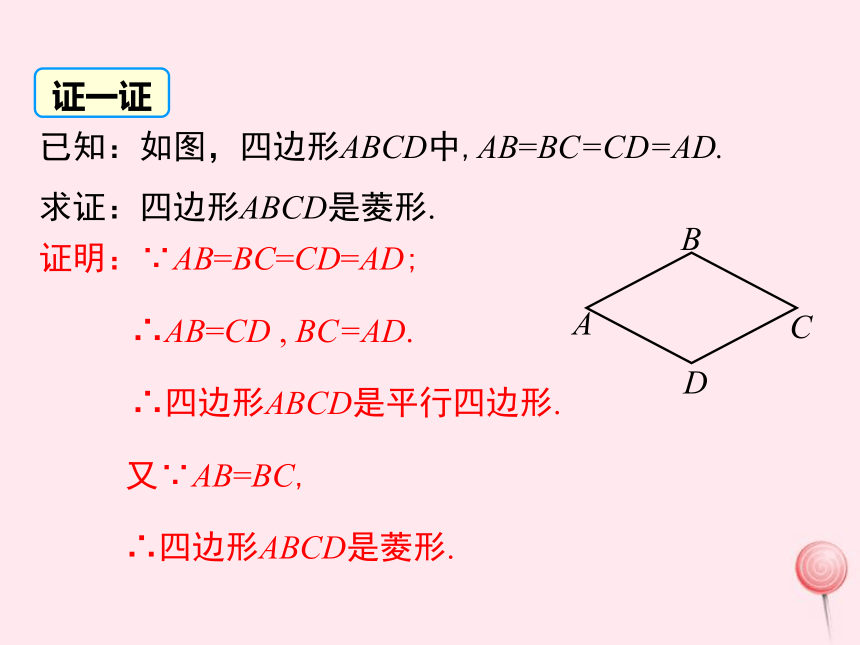
每一条对角线平分一组对角边角对角线复习引入导入新课问题 菱形的定义是什么?性质有哪些?根据菱形的定义,可得菱形的第一个判定的方法:AB=AD,∵四边形ABCD是平行四边形,∴四边形ABCD是菱形.数学语言有一组邻边相等的平行四边形叫做菱形.思考 还有其他的判定方法吗?小刚:分别以A、C为圆心,以大于 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点. 已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?CABD想一想:根据小刚的作法你有什么猜想?你能验证小刚的作法对吗? 猜想:四条边相等的四边形是菱形.讲授新课证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.已知:如图,四边形ABCD中,AB=BC=CD=AD.
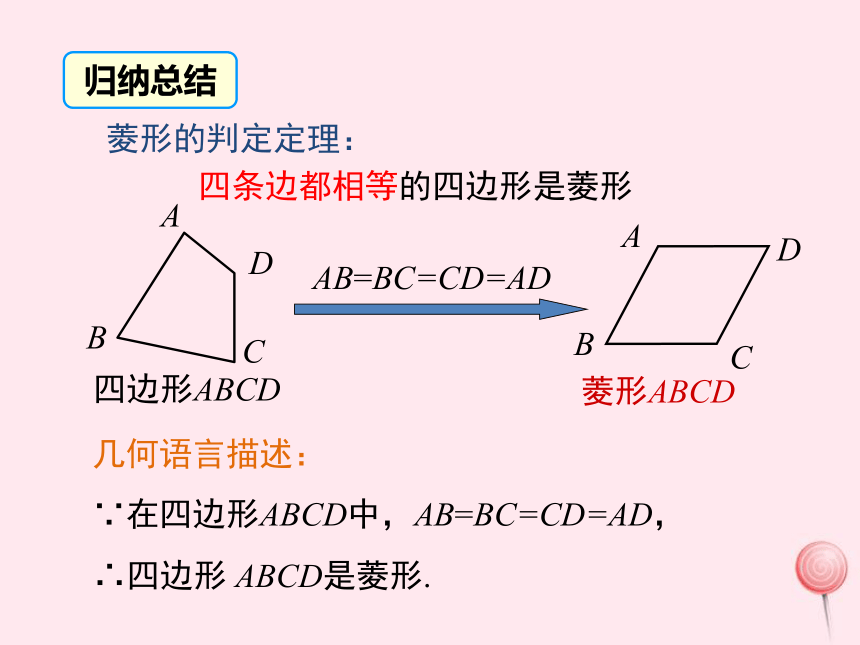
求证:四边形ABCD是菱形.证一证四条边都相等的四边形是菱形AB=BC=CD=AD几何语言描述:
∵在四边形ABCD中,AB=BC=CD=AD,∴四边形 ABCD是菱形.菱形的判定定理:归纳总结下列命题中正确的是 ( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
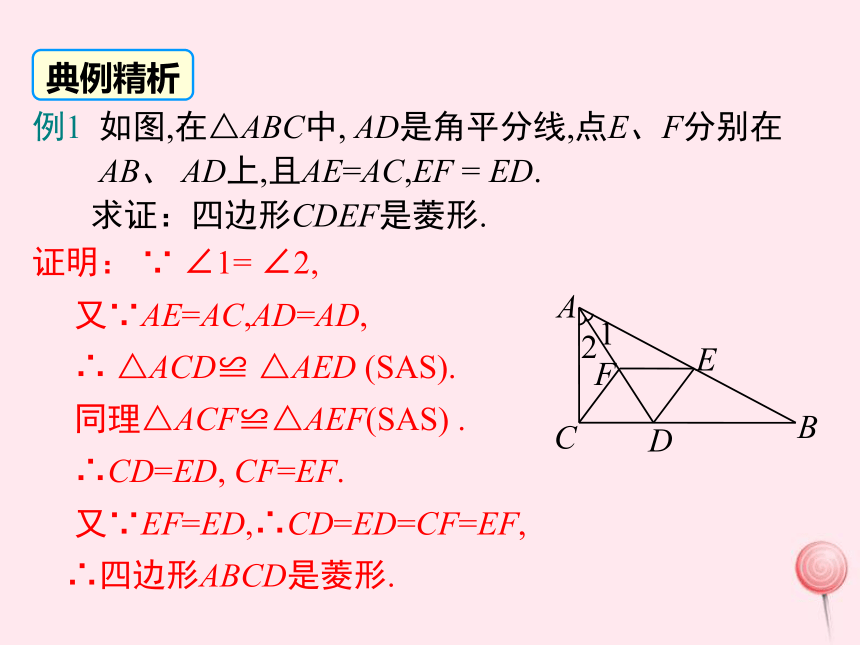
D.四个角相等的四边形是菱形C练一练证明: ∵ ∠1= ∠2,
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形ABCD是菱形.2例1 如图,在△ABC中, AD是角平分线,点E、F分别在
AB、 AD上,且AE=AC,EF = ED.
求证:四边形CDEF是菱形. ACBEDF1典例精析例2 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.证明:由平移变换的性质得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
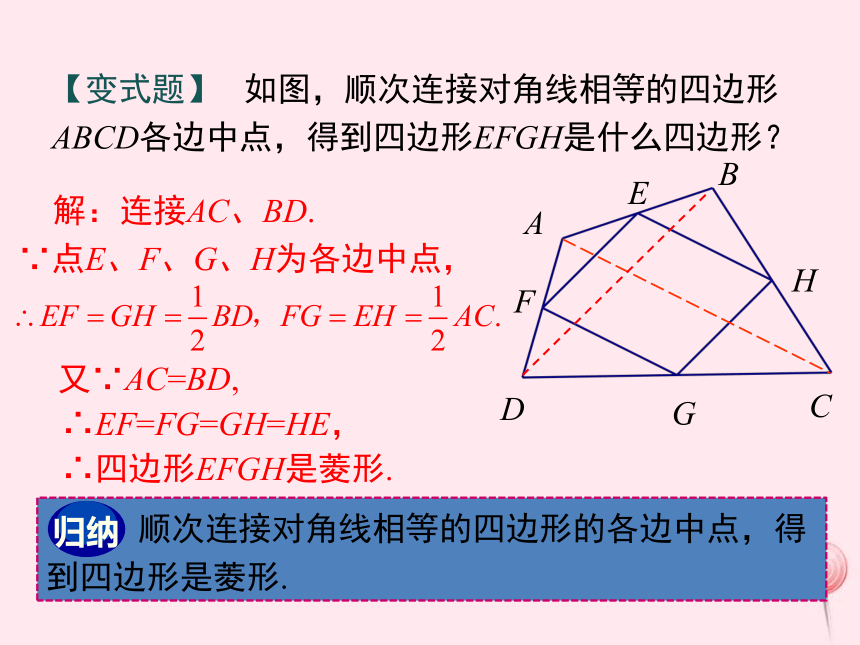
∴四边形ACFD是菱形. 四边形的条件中存在多个关于边的等量关系时,运用四条边都相等来判定一个四边形是菱形比较方便.证明:连接AC、BD.∵四边形ABCD是矩形,∴AC=BD.∵点E、F、G、H为各边中点,∴EF=FG=GH=HE,∴四边形EFGH是菱形.例3 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.【变式题】 如图,顺次连接对角线相等的四边形ABCD各边中点,得到四边形EFGH是什么四边形?解:连接AC、BD.又∵AC=BD,∵点E、F、G、H为各边中点,∴EF=FG=GH=HE,∴四边形EFGH是菱形. 顺次连接对角线相等的四边形的各边中点,得到四边形是菱形.拓展1 如图,顺次连接平行四边形ABCD各边中点,得到四边形EFGH是什么四边形?解:连接AC、BD.∵点E、F、G、H为各边中点,∴四边形EFGH是平行四边形.拓展2 如图,若四边形ABCD是菱形,顺次连接菱形ABCD各边中点,得到四边形EFGH是什么四边形?四边形EFGH是矩形.同学们自己去解答吧思考 在学平行四边形的时候我们知道把两张等宽的纸条交叉重叠在一起得到的四边形是平行四边形,你能进一步判断重叠部分ABCD的形状吗?ACDB分析:易知四边形ABCD是平行四边形,只需证一组邻边相等或对角线互相垂直即可.由题意可知BC边上的高和CD边上的高相等,然后通过证△ABE≌△ADF,即得AB=AD.请补充完整的证明过程EF前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形?对此你有什么猜想?猜想:对角线互相垂直的平行四边形是菱形.你能证明这一猜想吗?已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交 于点O ,AC⊥BD.
求证:□ABCD是菱形.证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).证一证对角线互相垂直的平行四边形是菱形几何语言描述:
∵在□ABCD中,AC⊥BD,∴ □ABCD是菱形.菱形的判定定理:归纳总结∴四边形ABCD是菱形.∵ OA=4,OB=3,AB=5,证明:即AC⊥BD,∴ AB2=OA2+OB2,∴△AOB是直角三角形,例5 如图,矩ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形. ABCDEFO12证明: ∵四边形ABCD是矩形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO = OC .
又∠AOE =∠COF,
∴△AOE≌△COF,∴EO =FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴ 四边形AFCE是菱形.练一练在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是 ( )
A.∠ABC=90°
B.AC⊥BD
C.AB=CD
D.AB∥CD B例6 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
又∵EF=BE,
∴四边形BCFE是菱形.(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .(2)若CE=4,∠BCF=120°,求菱形BCFE的面积. 判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以先尝试证出这个四边形是平行四边形.练一练如图,在平行四边形ABCD中,AC平分∠DAB,AB=2,求平行四边形ABCD的周长.解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,∠BAC=∠ACD,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠DAC=∠ACD,
∴AD=DC,
∴四边形ABCD为菱形,
∴四边形ABCD的周长=4×2=8.当堂练习1.判断下列说法是否正确
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等的
四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组
对角的四边形是菱形.√ ╳ ╳ ╳ 2.一边长为5cm平行四边形的两条对角线的长分别为
24cm和26cm,那么平行四边形的面积是 . 312cm23.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC
C.∠B=60° D.∠ACB=60° B解析:∵将△ABC沿BC方向平移得到△DCE,
∴AC∥DE,AC=DE,
∴四边形ACED为平行四边形.
当AC=BC时,
平行四边形ACED是菱形.
故选B.4.如图,矩形ABCD的对角线相交于点O,DE∥AC,
CE ∥BD.求证:四边形OCED是菱形.证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴OC=OD,
∴四边形OCED是菱形. 证明:∵MN是AC的垂直平分线,
∴AE=CE,AD=CD,OA=OC,
∠AOD=∠EOC=90°.
∵CE∥AB,
∴∠DAO=∠ECO,
∴△ADO≌△CEO(ASA).
∴AD=CE,OD=OE,
∵OD=OE,OA=OC,
∴四边形ADCE是平行四边形
又∵∠AOD=90°,∴四边形ADCE是菱形. 5.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.求证:四边形ADCE是菱形.BCN(1)证明:由尺规作∠BAF的平分线的过程可得AB=AF,∠BAE=∠FAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=BE,
∴BE=FA,∴四边形ABEF为平行四边形,
∵AB=AF,
∴四边形ABEF为菱形.6.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的
平分线交BC于点E,连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.解:∵四边形ABEF为菱形,
∴AE⊥BF,BO= FB=3,AE=2AO,
在Rt△AOB中,由勾股定理得AO =4,
∴AE=2AO=8.课堂小结有一组邻边相等的平行四边形是菱形.对角线互相垂直的平行四边形是菱形.四边相等的四边形是菱形.运用定理进行计算和证明菱形的判定定义法判定定理
定定理.(重点)
2.会用这些菱形的判定方法进行有关的证明和计算.
(难点)一组邻边相等有一组邻边相等的平行四边形叫做菱形菱形的性质菱形两组对边平行四条边相等两组对角分别相等 邻角互补两条对角线互相垂直平分
每一条对角线平分一组对角边角对角线复习引入导入新课问题 菱形的定义是什么?性质有哪些?根据菱形的定义,可得菱形的第一个判定的方法:AB=AD,∵四边形ABCD是平行四边形,∴四边形ABCD是菱形.数学语言有一组邻边相等的平行四边形叫做菱形.思考 还有其他的判定方法吗?小刚:分别以A、C为圆心,以大于 AC的长为半径作弧,两条 弧分别相交于点B , D,依次连接A、B、C、D四点. 已知线段AC,你能用尺规作图的方法作一个菱形ABCD,使AC为菱形的一条对角线吗?CABD想一想:根据小刚的作法你有什么猜想?你能验证小刚的作法对吗? 猜想:四条边相等的四边形是菱形.讲授新课证明:∵AB=BC=CD=AD;
∴AB=CD , BC=AD.
∴四边形ABCD是平行四边形.
又∵AB=BC,
∴四边形ABCD是菱形.已知:如图,四边形ABCD中,AB=BC=CD=AD.
求证:四边形ABCD是菱形.证一证四条边都相等的四边形是菱形AB=BC=CD=AD几何语言描述:
∵在四边形ABCD中,AB=BC=CD=AD,∴四边形 ABCD是菱形.菱形的判定定理:归纳总结下列命题中正确的是 ( )
A.一组邻边相等的四边形是菱形
B.三条边相等的四边形是菱形
C.四条边相等的四边形是菱形
D.四个角相等的四边形是菱形C练一练证明: ∵ ∠1= ∠2,
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形ABCD是菱形.2例1 如图,在△ABC中, AD是角平分线,点E、F分别在
AB、 AD上,且AE=AC,EF = ED.
求证:四边形CDEF是菱形. ACBEDF1典例精析例2 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.证明:由平移变换的性质得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形. 四边形的条件中存在多个关于边的等量关系时,运用四条边都相等来判定一个四边形是菱形比较方便.证明:连接AC、BD.∵四边形ABCD是矩形,∴AC=BD.∵点E、F、G、H为各边中点,∴EF=FG=GH=HE,∴四边形EFGH是菱形.例3 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.【变式题】 如图,顺次连接对角线相等的四边形ABCD各边中点,得到四边形EFGH是什么四边形?解:连接AC、BD.又∵AC=BD,∵点E、F、G、H为各边中点,∴EF=FG=GH=HE,∴四边形EFGH是菱形. 顺次连接对角线相等的四边形的各边中点,得到四边形是菱形.拓展1 如图,顺次连接平行四边形ABCD各边中点,得到四边形EFGH是什么四边形?解:连接AC、BD.∵点E、F、G、H为各边中点,∴四边形EFGH是平行四边形.拓展2 如图,若四边形ABCD是菱形,顺次连接菱形ABCD各边中点,得到四边形EFGH是什么四边形?四边形EFGH是矩形.同学们自己去解答吧思考 在学平行四边形的时候我们知道把两张等宽的纸条交叉重叠在一起得到的四边形是平行四边形,你能进一步判断重叠部分ABCD的形状吗?ACDB分析:易知四边形ABCD是平行四边形,只需证一组邻边相等或对角线互相垂直即可.由题意可知BC边上的高和CD边上的高相等,然后通过证△ABE≌△ADF,即得AB=AD.请补充完整的证明过程EF前面我们用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个平行四边形.那么转动木条,这个平行四边形什么时候变成菱形?对此你有什么猜想?猜想:对角线互相垂直的平行四边形是菱形.你能证明这一猜想吗?已知:如图,四边形ABCD是平行四边形,对角线AC与BD相交 于点O ,AC⊥BD.
求证:□ABCD是菱形.证明: ∵四边形ABCD是平行四边形.
∴OA=OC.
又∵AC⊥BD,
∴BD是线段AC的垂直平分线.
∴BA=BC.
∴四边形ABCD是菱形(菱形的定义).证一证对角线互相垂直的平行四边形是菱形几何语言描述:
∵在□ABCD中,AC⊥BD,∴ □ABCD是菱形.菱形的判定定理:归纳总结∴四边形ABCD是菱形.∵ OA=4,OB=3,AB=5,证明:即AC⊥BD,∴ AB2=OA2+OB2,∴△AOB是直角三角形,例5 如图,矩ABCD的对角线AC的垂直平分线与边AD、BC分别交于点E、F,求证:四边形AFCE是菱形. ABCDEFO12证明: ∵四边形ABCD是矩形,
∴AE∥FC,∴∠1=∠2.
∵EF垂直平分AC,
∴AO = OC .
又∠AOE =∠COF,
∴△AOE≌△COF,∴EO =FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC
∴ 四边形AFCE是菱形.练一练在四边形ABCD中,对角线AC,BD互相平分,若添加一个条件使得四边形ABCD是菱形,则这个条件可以是 ( )
A.∠ABC=90°
B.AC⊥BD
C.AB=CD
D.AB∥CD B例6 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
又∵EF=BE,
∴四边形BCFE是菱形.(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .(2)若CE=4,∠BCF=120°,求菱形BCFE的面积. 判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以先尝试证出这个四边形是平行四边形.练一练如图,在平行四边形ABCD中,AC平分∠DAB,AB=2,求平行四边形ABCD的周长.解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,∠BAC=∠ACD,
∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠DAC=∠ACD,
∴AD=DC,
∴四边形ABCD为菱形,
∴四边形ABCD的周长=4×2=8.当堂练习1.判断下列说法是否正确
(1)对角线互相垂直的四边形是菱形;
(2)对角线互相垂直且平分的四边形是菱形;
(3)对角线互相垂直,且有一组邻边相等的
四边形是菱形;
(4)两条邻边相等,且一条对角线平分一组
对角的四边形是菱形.√ ╳ ╳ ╳ 2.一边长为5cm平行四边形的两条对角线的长分别为
24cm和26cm,那么平行四边形的面积是 . 312cm23.如图,将△ABC沿BC方向平移得到△DCE,连接AD,下列条件能够判定四边形ACED为菱形的是( )
A.AB=BC B.AC=BC
C.∠B=60° D.∠ACB=60° B解析:∵将△ABC沿BC方向平移得到△DCE,
∴AC∥DE,AC=DE,
∴四边形ACED为平行四边形.
当AC=BC时,
平行四边形ACED是菱形.
故选B.4.如图,矩形ABCD的对角线相交于点O,DE∥AC,
CE ∥BD.求证:四边形OCED是菱形.证明:∵DE∥AC,CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴OC=OD,
∴四边形OCED是菱形. 证明:∵MN是AC的垂直平分线,
∴AE=CE,AD=CD,OA=OC,
∠AOD=∠EOC=90°.
∵CE∥AB,
∴∠DAO=∠ECO,
∴△ADO≌△CEO(ASA).
∴AD=CE,OD=OE,
∵OD=OE,OA=OC,
∴四边形ADCE是平行四边形
又∵∠AOD=90°,∴四边形ADCE是菱形. 5.如图,△ABC中,AC的垂直平分线MN交AB于点D,交AC于点O,CE∥AB交MN于点E,连接AE、CD.求证:四边形ADCE是菱形.BCN(1)证明:由尺规作∠BAF的平分线的过程可得AB=AF,∠BAE=∠FAE,
∵四边形ABCD是平行四边形,
∴AD∥BC,∴∠FAE=∠AEB,
∴∠BAE=∠AEB,∴AB=BE,
∴BE=FA,∴四边形ABEF为平行四边形,
∵AB=AF,
∴四边形ABEF为菱形.6.如图,在平行四边形ABCD中,用直尺和圆规作∠BAD的
平分线交BC于点E,连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.解:∵四边形ABEF为菱形,
∴AE⊥BF,BO= FB=3,AE=2AO,
在Rt△AOB中,由勾股定理得AO =4,
∴AE=2AO=8.课堂小结有一组邻边相等的平行四边形是菱形.对角线互相垂直的平行四边形是菱形.四边相等的四边形是菱形.运用定理进行计算和证明菱形的判定定义法判定定理
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
