冀教版2019秋八年级数学下册第二十二章四边形小结与复习课件(36张PPT)
文档属性
| 名称 | 冀教版2019秋八年级数学下册第二十二章四边形小结与复习课件(36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 276.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-20 22:16:49 | ||
图片预览








文档简介
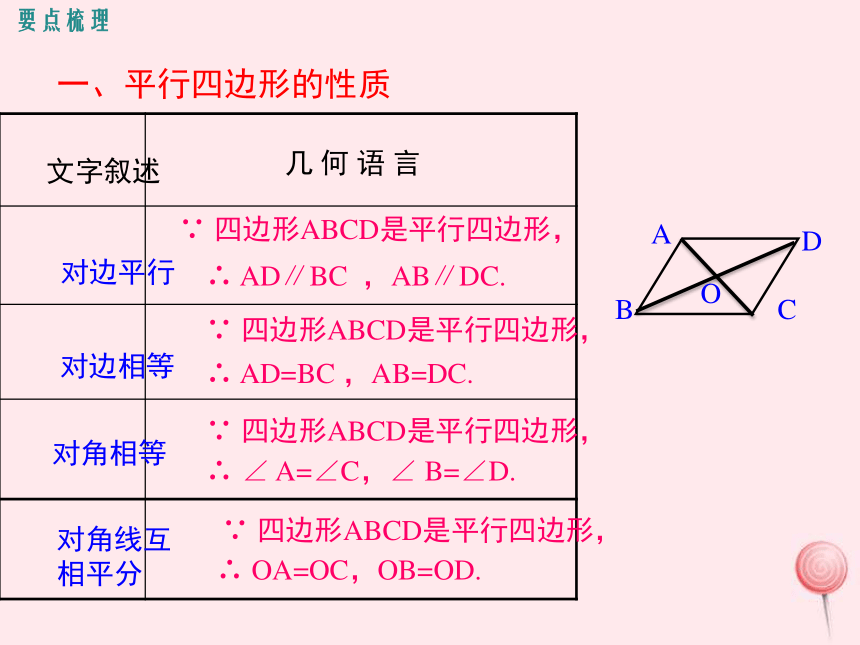
课件36张PPT。小结与复习第二十二章 四边形要点梳理考点讲练课堂小结课后作业几 何 语 言文字叙述对边平行对边相等对角相等∴ AD=BC ,AB=DC.∵ 四边形ABCD是平行四边形, ∴ ∠ A=∠C,∠ B=∠D.∵ 四边形ABCD是平行四边形, 一、平行四边形的性质对角线互
相平分∵ 四边形ABCD是平行四边形, ∴ OA=OC,OB=OD.∵ 四边形ABCD是平行四边形, ∴ AD∥BC ,AB∥DC.要点梳理O几 何 语 言文字叙述两组对边相等一组对边平行且相等 ∴四边形ABCD是平行四边形, ∵ AD=BC ,AB=DC.∴ 四边形ABCD是平行四边形, ∵ AB=DC,AB∥DC.二、平行四边形的判定对角线互相平分∴ 四边形ABCD是平行四边形, ∵ OA=OC,OB=OD.两组对边分别平行(定义)∴ 四边形ABCD是平行四边形, ∵ AD∥BC ,AB∥DC.O1.三角形的中位线定义:连接三角形两边中点的线段叫做三角形的中位线.2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.三、三角形的中位线用符号语言表示∵DE是△ABC的中位线∴DE∥BC,平行且相等平行
且四边相等平行
且四边相等四个角
都是直角对角相等
邻角互补四个角
都是直角互相平分且相等互相垂直平分且相等,每一条对角线平分一组对角互相垂直且平分,每一条对角线平分一组对角四、矩形、菱形、正方形的性质①定义:有一角是直角的平行四边形
②三个角是直角的四边形
③对角线相等的平行四边形①定义:一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形①定义:一组邻边相等且有一个角是直角的平行四边形
②有一组邻边相等的矩形
③有一个角是直角的菱形五、矩形、菱形、正方形的判定方法六、多边形的内角和与外角和多边形的内角和等于(n-2) ×180 °
多边形的外角和等于 360 °
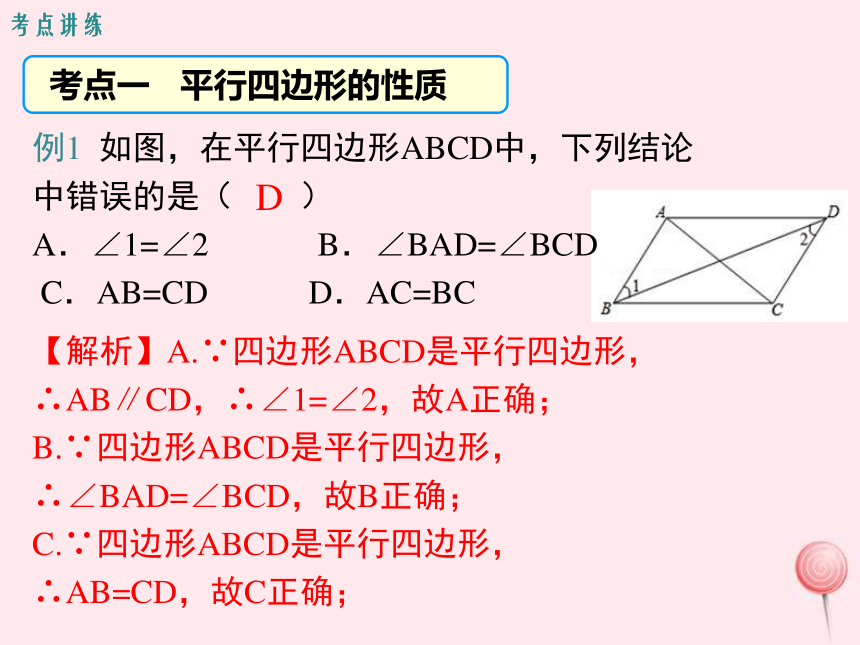
例1 如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC=BC 【解析】A.∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠1=∠2,故A正确;
B.∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,故B正确;
C.∵四边形ABCD是平行四边形,
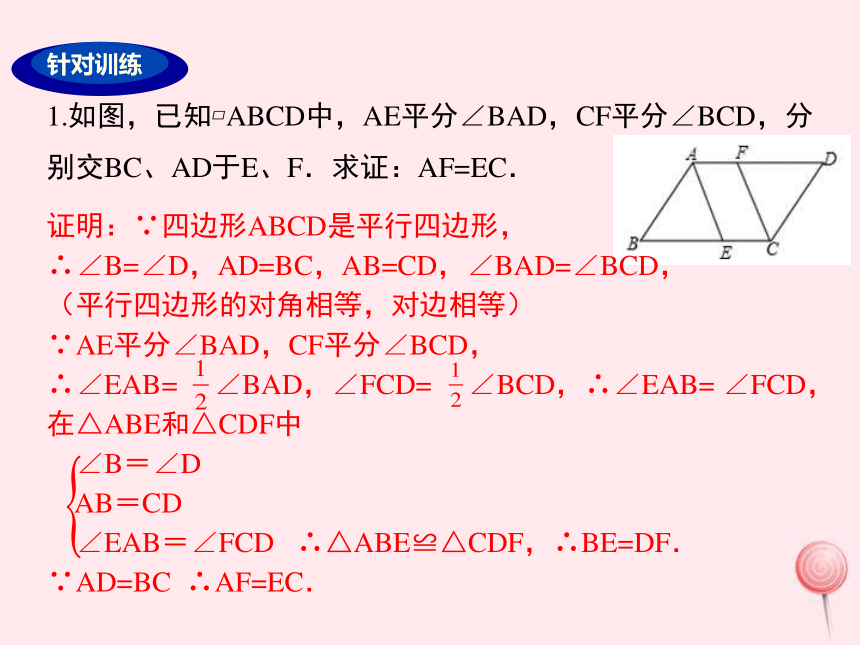
∴AB=CD,故C正确;D考点讲练 主要考查了平行四边形的性质,关键是掌握平行四边形对边相等且平行,对角相等.1.如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:AF=EC.证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AD=BC,AB=CD,∠BAD=∠BCD,
(平行四边形的对角相等,对边相等)
∵AE平分∠BAD,CF平分∠BCD,
∴∠EAB= ∠BAD,∠FCD= ∠BCD,∴∠EAB= ∠FCD,
在△ABE和△CDF中
∠B=∠D
AB=CD
∠EAB=∠FCD ∴△ABE≌△CDF,∴BE=DF.
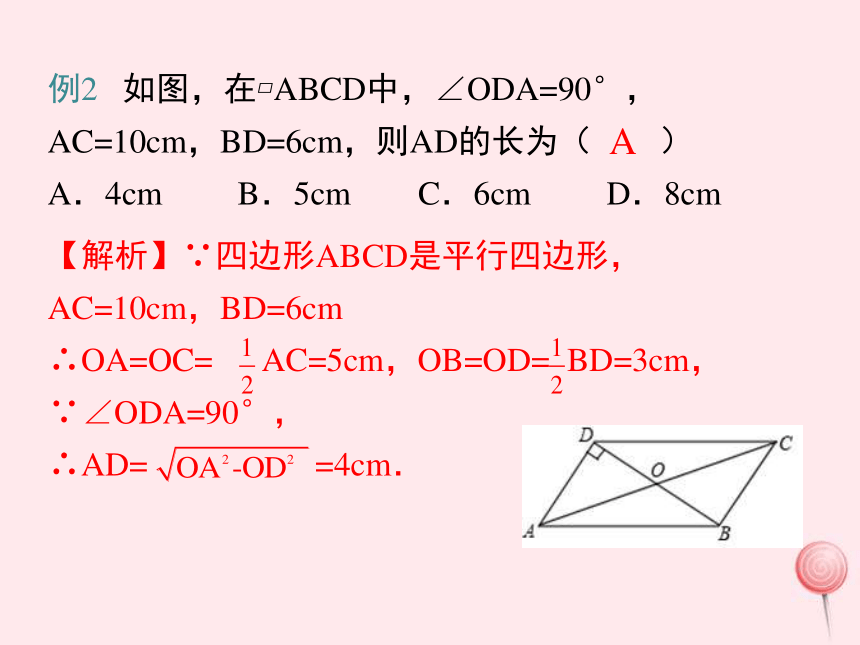
∵AD=BC ∴AF=EC.例2 如图,在?ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4cm B.5cm C.6cm D.8cm 【解析】∵四边形ABCD是平行四边形,
AC=10cm,BD=6cm
∴OA=OC= AC=5cm,OB=OD= BD=3cm,
∵∠ODA=90°,
∴AD= =4cm.A 主要考查了平行四边形的性质,平行四边形的对角线互相平分,解题时还要注意勾股定理的应用.【解析】∵在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,
∴AO=CO=12cm,BO=19cm,AD=BC=28cm,
∴△BOC的周长是:BO+CO+BC=12+19+28=59(cm).2.如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
A.45cm B.59cm C.62cm D.90cm B例3 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO D 平行四边形的判定方法:
①两组对边分别平行的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③两组对角分别相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形;
⑤一组对边平行且相等的四边形是平行四边形.3.如图,点D、C在BF上,AC∥DE,∠A=∠E,BD=CF,
(1)求证:AB=EF.(1)证明:∵AC∥DE,
∴∠ACD=∠EDF,
∵BD=CF,∴BD+DC=CF+DC,
即BC=DF,
又∵∠A=∠E,∴△ABC≌△EFD(AAS),
∴AB=EF.(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由.(2)猜想:四边形ABEF为平行四边形,
理由如下:由(1)知△ABC≌△EFD,
∴∠B=∠F,∴AB∥EF,
又∵AB=EF,
四边形ABEF为平行四边形(一组对边平行且相等的四边形是平行四边形).例4 已知:AD是△ABC的中线,E是AD的中点,F是BE的延长线与AC的交点。求证: . 证明:过点D作DH∥BF,交AC于点H.
∵AD是△ABC的中线.
∴D是BC的中点.
∴CH=HF= CF
∵E是AD的中点,EF∥DH.
∴AF=FH.
∴AF= FCABCDEFH4.若三角形的三条中位线之比为 6 : 5 : 4 ,三角形的周长为 60 cm,那么该三角形中最长边的边长为___;解析:设三角形的三条中位线之长分别为6x,5x,4x,
则三角形的三条边长之长分别为12x,10x,8x,
依题意有 12x+10x+8x=60,解得 x=2.所以,最长边12x=24(cm).24 cm例5:如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5 ,求矩形对角线的长.解:∵四边形ABCD是矩形.
∴AC = BD(矩形的对角线相等).
OA= OC= AC,OB = OD = BD ,
(矩形对角线相互平分)
∴OA = OD.ABCDO∵∠AOD=120°,
∴∠ODA=∠OAD= (180°- 120°)=30°.
又∵∠DAB=90° ,
(矩形的四个角都是直角)
∴BD = 2AB = 2 ×2.5 = 5.5.如图,在□ABCD中,对角线AC与BD相交于点O , △ABO是等边三角形, AB=4,求□ABCD的面积.
解:∵四边形ABCD是平行四边形,
∴OA= OC,OB = OD.
又∵△ABO是等边三角形,
∴OA= OB=AB= 4,∠BAC=60°.
∴AC= BD= 2OA = 2×4 = 8.∴□ABCD是矩形 (对角线相等的平行四边形是矩形).
∴∠ABC=90°(矩形的四个角都是直角) .
在Rt△ABC中,由勾股定理,得
AB2 + BC2 =AC2 ,
∴BC= .
∴S□ABCD=AB·BC=4× =6.如图,O是菱形ABCD对角线的交点,作BE∥AC,CE∥BD,BE、CE交于点E,四边形CEBO是矩形吗?说出你的理由.DABCEO解:四边形CEBO是矩形.
理由如下:已知四边形ABCD是菱形.
∴AC⊥BD.
∴∠BOC=90°.
∵DE∥AC,CE∥BD,
∴四边形CEBO是平行四边形.
∴四边形CEBO是矩形(有一个角是直角的平行四边形是矩形).例7:如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD =6,求菱形的边长AB和对角线AC的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD(菱形的对角线互相垂直)
OB=OD= BD = ×6=3(菱形的对角线互相平分)
在等腰三角形ABC中,
∵∠BAD=60°,
∴△ABD是等边三角形.
∴AB = BD = 6. AO= AC=证明:在△AOB中.
∵AB= , OA=2,OB=1.
∴AB2=AO2+OB2.
∴ △AOB是直角三角形, ∠AOB是直角.
∴AC⊥BD.
∴ □ABCD是菱形
(对角线垂直的平行四边形是菱形).7. 已知:如右图,在□ABCD中,对角线AC与BD相交于点O, AB= ,OA=2,OB=1. 求证: □ABCD是菱形.8.如图,两张等宽的纸条交叉重叠在一起,猜想重叠部分的四边形ABCD是什么形状?说说你的理由.ABCDEF解:四边形ABCD是菱形.
过点C作AB边的垂线交点E,作AD边上的垂线交点F.
S 四边形ABCD=AD · CF =AB ·CE .
由题意可知 CE = CF 且 四边形ABCD是平行四边形.
∴AD = AB .
∴四边形ABCD是菱形.例8:如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系?请说明理由.解:BE=DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD是正方形.
∴BC=DC,∠BCE =90° .
(正方形的四条边都相等,四个角都是直角)
∴∠DCF=180°-∠BCE=180°-90°=90°.ABDCFE∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.
(2)延长BE交DE于点M,
∵△BCE≌△DCF ,
∴∠CBE =∠CDF.
∵∠DCF =90° ,
∴∠CDF +∠F =90°.∴∠CBE+∠F=90° , ∴∠BMF=90°.
∴BE⊥DF.ABDFECM9. 如图,在矩形ABCD中, BE平分∠ABC , CE平分∠DCB , BF∥CE , CF∥BE.
求证:四边形BECF是正方形.FABECD解析:先由两组平行线得出四边形BECF平行四边形;再由一个直角,得出是矩形;最后由一组邻边相等可得正方形.45°45°FABECD证明: ∵ BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴ ∠ABC = 90°, ∠DCB = 90°,
∵BE平分∠ABC, CE平分∠ DCB,
∴∠EBC = 45°, ∠ECB = 45°,
∴ ∠ EBC =∠ ECB .
∴ EB=EC,∴□ BECF是菱形 .
在△EBC中
∵ ∠EBC = 45°,∠ECB = 45°,
∴∠BEC = 90°,
∴菱形BECF是正方形.(有一个角是直角的菱形是正方形)例9:已知一个多边形的每个外角都是其相邻内角度数的 ,求这个多边形的边数. 解: 设此多边形的外角的度数为x,则内角的度数为4x,
则x+4x=180°,解得 x=36°.
∴边数n=360°÷36°=10.10.一个正多边形的每一个内角都等于120 °,则其边数是 .6【解析】 因为该多边形的每一个内角都等于120度,所以它的每一个外角都等于60 °.所以边数是6. 在多边形的有关求边数或内角、外角度数的问题中,要注意内角与外角之间的转化,以及定理的运用.尤其在求边数的问题中,常常利用定理列出方程,进而再求得边数.平 行 四 边 形性质①对边平行且相等②对角相等,邻角互补③对角线互相平分
判定①两组对边分别平行的②两组对边分别相等的③一组对边平行且相等的④对角线互相平分的
四 边 形课堂小结三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.多边形的内角和与外角和内角和计算公式(n-2) × 180 °(n ≥3的整数) 外角和多边形的外角和等于360°
特别注意:与边数无关有一个角是90°
(或对角线相等)有一对邻边相等
(或对角线互相垂直) 平行四边形矩形菱形正方形一组邻边相等且一个内角为直角
(或对角线互相垂直且相等)有一个角是90°
(或对角线相等)有一对邻边相等
(或对角线互相垂直) 课堂小结
相平分∵ 四边形ABCD是平行四边形, ∴ OA=OC,OB=OD.∵ 四边形ABCD是平行四边形, ∴ AD∥BC ,AB∥DC.要点梳理O几 何 语 言文字叙述两组对边相等一组对边平行且相等 ∴四边形ABCD是平行四边形, ∵ AD=BC ,AB=DC.∴ 四边形ABCD是平行四边形, ∵ AB=DC,AB∥DC.二、平行四边形的判定对角线互相平分∴ 四边形ABCD是平行四边形, ∵ OA=OC,OB=OD.两组对边分别平行(定义)∴ 四边形ABCD是平行四边形, ∵ AD∥BC ,AB∥DC.O1.三角形的中位线定义:连接三角形两边中点的线段叫做三角形的中位线.2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.三、三角形的中位线用符号语言表示∵DE是△ABC的中位线∴DE∥BC,平行且相等平行
且四边相等平行
且四边相等四个角
都是直角对角相等
邻角互补四个角
都是直角互相平分且相等互相垂直平分且相等,每一条对角线平分一组对角互相垂直且平分,每一条对角线平分一组对角四、矩形、菱形、正方形的性质①定义:有一角是直角的平行四边形
②三个角是直角的四边形
③对角线相等的平行四边形①定义:一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形①定义:一组邻边相等且有一个角是直角的平行四边形
②有一组邻边相等的矩形
③有一个角是直角的菱形五、矩形、菱形、正方形的判定方法六、多边形的内角和与外角和多边形的内角和等于(n-2) ×180 °
多边形的外角和等于 360 °
例1 如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC=BC 【解析】A.∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠1=∠2,故A正确;
B.∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,故B正确;
C.∵四边形ABCD是平行四边形,
∴AB=CD,故C正确;D考点讲练 主要考查了平行四边形的性质,关键是掌握平行四边形对边相等且平行,对角相等.1.如图,已知?ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:AF=EC.证明:∵四边形ABCD是平行四边形,
∴∠B=∠D,AD=BC,AB=CD,∠BAD=∠BCD,
(平行四边形的对角相等,对边相等)
∵AE平分∠BAD,CF平分∠BCD,
∴∠EAB= ∠BAD,∠FCD= ∠BCD,∴∠EAB= ∠FCD,
在△ABE和△CDF中
∠B=∠D
AB=CD
∠EAB=∠FCD ∴△ABE≌△CDF,∴BE=DF.
∵AD=BC ∴AF=EC.例2 如图,在?ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4cm B.5cm C.6cm D.8cm 【解析】∵四边形ABCD是平行四边形,
AC=10cm,BD=6cm
∴OA=OC= AC=5cm,OB=OD= BD=3cm,
∵∠ODA=90°,
∴AD= =4cm.A 主要考查了平行四边形的性质,平行四边形的对角线互相平分,解题时还要注意勾股定理的应用.【解析】∵在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,
∴AO=CO=12cm,BO=19cm,AD=BC=28cm,
∴△BOC的周长是:BO+CO+BC=12+19+28=59(cm).2.如图,在?ABCD中,对角线AC和BD交于点O,AC=24cm,BD=38cm,AD=28cm,则△BOC的周长是( )
A.45cm B.59cm C.62cm D.90cm B例3 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO D 平行四边形的判定方法:
①两组对边分别平行的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③两组对角分别相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形;
⑤一组对边平行且相等的四边形是平行四边形.3.如图,点D、C在BF上,AC∥DE,∠A=∠E,BD=CF,
(1)求证:AB=EF.(1)证明:∵AC∥DE,
∴∠ACD=∠EDF,
∵BD=CF,∴BD+DC=CF+DC,
即BC=DF,
又∵∠A=∠E,∴△ABC≌△EFD(AAS),
∴AB=EF.(2)连接AF,BE,猜想四边形ABEF的形状,并说明理由.(2)猜想:四边形ABEF为平行四边形,
理由如下:由(1)知△ABC≌△EFD,
∴∠B=∠F,∴AB∥EF,
又∵AB=EF,
四边形ABEF为平行四边形(一组对边平行且相等的四边形是平行四边形).例4 已知:AD是△ABC的中线,E是AD的中点,F是BE的延长线与AC的交点。求证: . 证明:过点D作DH∥BF,交AC于点H.
∵AD是△ABC的中线.
∴D是BC的中点.
∴CH=HF= CF
∵E是AD的中点,EF∥DH.
∴AF=FH.
∴AF= FCABCDEFH4.若三角形的三条中位线之比为 6 : 5 : 4 ,三角形的周长为 60 cm,那么该三角形中最长边的边长为___;解析:设三角形的三条中位线之长分别为6x,5x,4x,
则三角形的三条边长之长分别为12x,10x,8x,
依题意有 12x+10x+8x=60,解得 x=2.所以,最长边12x=24(cm).24 cm例5:如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5 ,求矩形对角线的长.解:∵四边形ABCD是矩形.
∴AC = BD(矩形的对角线相等).
OA= OC= AC,OB = OD = BD ,
(矩形对角线相互平分)
∴OA = OD.ABCDO∵∠AOD=120°,
∴∠ODA=∠OAD= (180°- 120°)=30°.
又∵∠DAB=90° ,
(矩形的四个角都是直角)
∴BD = 2AB = 2 ×2.5 = 5.5.如图,在□ABCD中,对角线AC与BD相交于点O , △ABO是等边三角形, AB=4,求□ABCD的面积.
解:∵四边形ABCD是平行四边形,
∴OA= OC,OB = OD.
又∵△ABO是等边三角形,
∴OA= OB=AB= 4,∠BAC=60°.
∴AC= BD= 2OA = 2×4 = 8.∴□ABCD是矩形 (对角线相等的平行四边形是矩形).
∴∠ABC=90°(矩形的四个角都是直角) .
在Rt△ABC中,由勾股定理,得
AB2 + BC2 =AC2 ,
∴BC= .
∴S□ABCD=AB·BC=4× =6.如图,O是菱形ABCD对角线的交点,作BE∥AC,CE∥BD,BE、CE交于点E,四边形CEBO是矩形吗?说出你的理由.DABCEO解:四边形CEBO是矩形.
理由如下:已知四边形ABCD是菱形.
∴AC⊥BD.
∴∠BOC=90°.
∵DE∥AC,CE∥BD,
∴四边形CEBO是平行四边形.
∴四边形CEBO是矩形(有一个角是直角的平行四边形是矩形).例7:如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD =6,求菱形的边长AB和对角线AC的长.
解:∵四边形ABCD是菱形,
∴AC⊥BD(菱形的对角线互相垂直)
OB=OD= BD = ×6=3(菱形的对角线互相平分)
在等腰三角形ABC中,
∵∠BAD=60°,
∴△ABD是等边三角形.
∴AB = BD = 6. AO= AC=证明:在△AOB中.
∵AB= , OA=2,OB=1.
∴AB2=AO2+OB2.
∴ △AOB是直角三角形, ∠AOB是直角.
∴AC⊥BD.
∴ □ABCD是菱形
(对角线垂直的平行四边形是菱形).7. 已知:如右图,在□ABCD中,对角线AC与BD相交于点O, AB= ,OA=2,OB=1. 求证: □ABCD是菱形.8.如图,两张等宽的纸条交叉重叠在一起,猜想重叠部分的四边形ABCD是什么形状?说说你的理由.ABCDEF解:四边形ABCD是菱形.
过点C作AB边的垂线交点E,作AD边上的垂线交点F.
S 四边形ABCD=AD · CF =AB ·CE .
由题意可知 CE = CF 且 四边形ABCD是平行四边形.
∴AD = AB .
∴四边形ABCD是菱形.例8:如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系?请说明理由.解:BE=DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD是正方形.
∴BC=DC,∠BCE =90° .
(正方形的四条边都相等,四个角都是直角)
∴∠DCF=180°-∠BCE=180°-90°=90°.ABDCFE∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.
(2)延长BE交DE于点M,
∵△BCE≌△DCF ,
∴∠CBE =∠CDF.
∵∠DCF =90° ,
∴∠CDF +∠F =90°.∴∠CBE+∠F=90° , ∴∠BMF=90°.
∴BE⊥DF.ABDFECM9. 如图,在矩形ABCD中, BE平分∠ABC , CE平分∠DCB , BF∥CE , CF∥BE.
求证:四边形BECF是正方形.FABECD解析:先由两组平行线得出四边形BECF平行四边形;再由一个直角,得出是矩形;最后由一组邻边相等可得正方形.45°45°FABECD证明: ∵ BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴ ∠ABC = 90°, ∠DCB = 90°,
∵BE平分∠ABC, CE平分∠ DCB,
∴∠EBC = 45°, ∠ECB = 45°,
∴ ∠ EBC =∠ ECB .
∴ EB=EC,∴□ BECF是菱形 .
在△EBC中
∵ ∠EBC = 45°,∠ECB = 45°,
∴∠BEC = 90°,
∴菱形BECF是正方形.(有一个角是直角的菱形是正方形)例9:已知一个多边形的每个外角都是其相邻内角度数的 ,求这个多边形的边数. 解: 设此多边形的外角的度数为x,则内角的度数为4x,
则x+4x=180°,解得 x=36°.
∴边数n=360°÷36°=10.10.一个正多边形的每一个内角都等于120 °,则其边数是 .6【解析】 因为该多边形的每一个内角都等于120度,所以它的每一个外角都等于60 °.所以边数是6. 在多边形的有关求边数或内角、外角度数的问题中,要注意内角与外角之间的转化,以及定理的运用.尤其在求边数的问题中,常常利用定理列出方程,进而再求得边数.平 行 四 边 形性质①对边平行且相等②对角相等,邻角互补③对角线互相平分
判定①两组对边分别平行的②两组对边分别相等的③一组对边平行且相等的④对角线互相平分的
四 边 形课堂小结三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.多边形的内角和与外角和内角和计算公式(n-2) × 180 °(n ≥3的整数) 外角和多边形的外角和等于360°
特别注意:与边数无关有一个角是90°
(或对角线相等)有一对邻边相等
(或对角线互相垂直) 平行四边形矩形菱形正方形一组邻边相等且一个内角为直角
(或对角线互相垂直且相等)有一个角是90°
(或对角线相等)有一对邻边相等
(或对角线互相垂直) 课堂小结
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
