2.2.1 函数的单调性 课件 47张PPT
文档属性
| 名称 | 2.2.1 函数的单调性 课件 47张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 19:48:04 | ||
图片预览







文档简介
课件47张PPT。函数的单调性教学目标
教学重点与难点??
? 1.从形与数两方面理解函数单调性的概念,初步掌握利用函数图象和单调性定义判断、证明函数单调性的方法.
2.通过对函数单调性定义的探究,渗透数形结合数学思想方法,培养学生观察、归纳、抽象的能力和语言表达能力;通过对函数单调性的证明,提高学生的推理论证能力.
3.通过知识的探究过程培养学生细心观察、认真分析、严谨论证的良好思维习惯,让学生经历从具体到抽象,从特殊到一般,从感性到理性的认知过程.【教学目标】【教学重点】?函数单调性的概念、判断及证明.
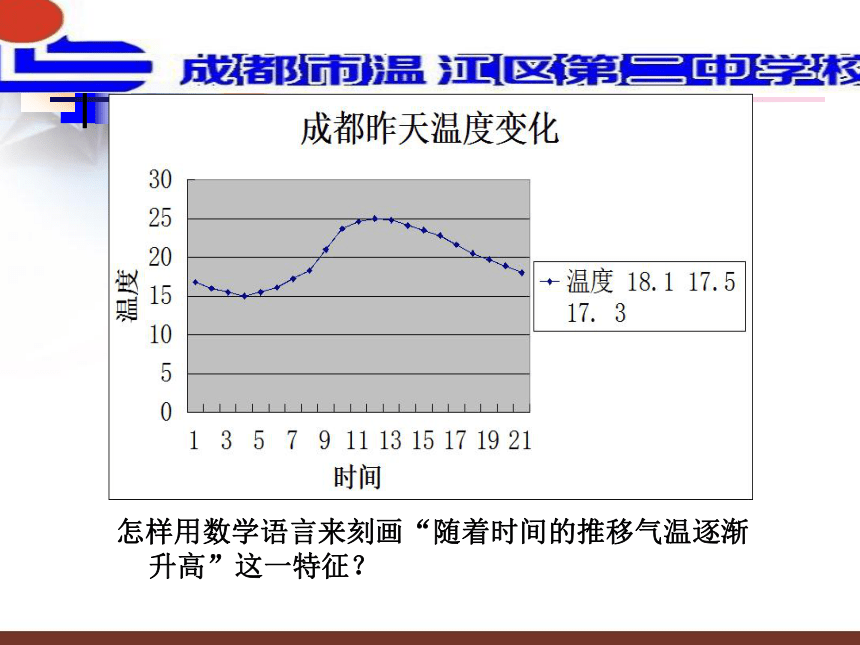
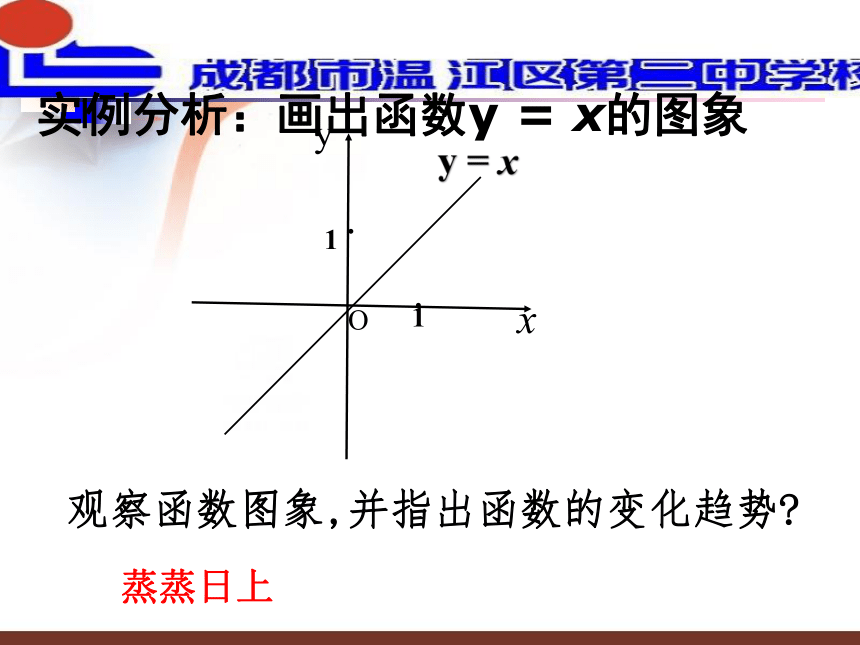
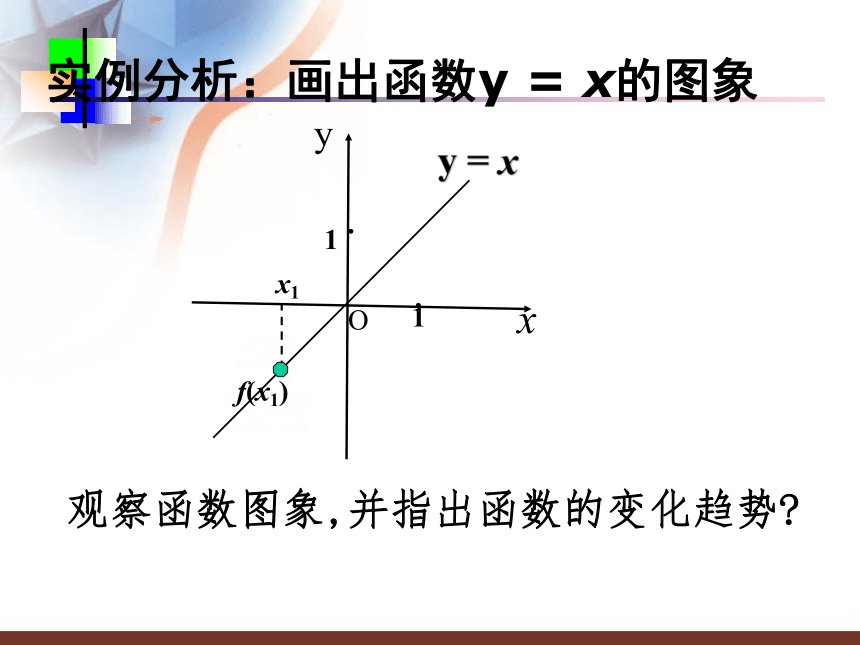
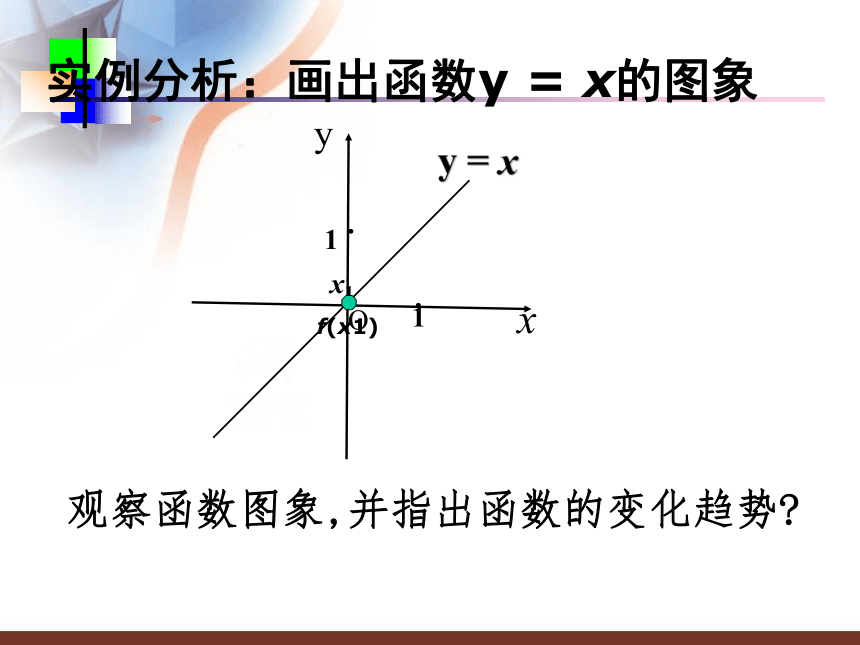
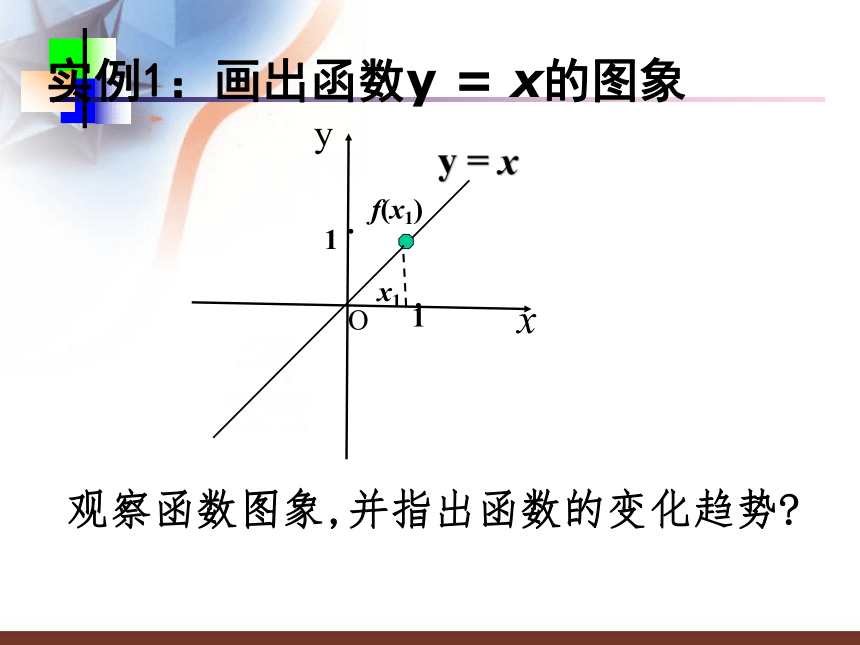
【教学难点】?归纳抽象函数单调性的定义以及根据定义证明函数的单调性.怎样用数学语言来刻画“随着时间的推移气温逐渐升高”这一特征?xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?蒸蒸日上xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?f(x1)x1xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?x1f(x1)xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?x1f(x1)xyy = xO11··实例1:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?x1f(x1)xyy = xO11··x1f(x1)实例1:画出函数y = x的图象xyy = xO11··x1f(x1)1.从左至右图象上升还是下降 ____?
2.在区间 ________上,随着x的增大,f(x)的值随着 ______ .上升(-∞, +∞)增大实例2:画出函数 图像(反比例函数)每况愈下Oxy实例3:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象观察函数图象,并指出函数的变化趋势?Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象1.在区间_______上,f(x)的值随着x的增大而_____.
2. 在区间_______上,f(x)的值随着x的增大而 _____. (-∞, 0](0, +∞)增大减小xyO此起彼伏看图结语 不同的函数,其图像的变化趋势可能不同,同一函数在不同的区间上变化趋势也不一定相同,函数的这种变化规律反映了函数的一个重要性质,即函数的单调性。函数单调性定义 一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x10, f(x)依然为在区间D上的增函数。1.增函数形:图像呈上升趋势
数:x不断增大,y也不断增大共同进退→ 一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1f(x2),那么就说f(x)在区间D上是减函数 .或者有 (f(x1)- f(x2)/(x1-x2)<0, f(x)依然为在区间D上的减函数。2.减函数 此消彼长 3.函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;注意:2.必须是对于区间D内的任意两个自变量x1,x2;当x1f(x2) 分别是增函数和减函数.1.如果函数 y =f(x)在区间D是单调增函数或单调减函数,那么就说函数 y =f(x)在区间D上具有单调性。4.区间D一定是指x的取值范围。如果函数 在区间 和 都是单调减函数,能否说 在定义域 内递增?思考?单调性是函数的局部性质单调性是对定义域中的任意x而言 有几个单调区间之时,每个单调区间之间一定要用逗号隔开或者用“和”字连接。
比如某个函数单调增区间为(2,5)和(7,9),必须写成(2,5)和(7,9),或(2,5),(7,9)。注意:例1.下图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每个区间上,它是增函数还是减函数?解:函数y=f(x)的单调区间有其中y=f(x)在区间[-5, -2), [1, 3)上是减函数,
在区间[-2, 1), [3, 5] 上是增函数.[-5, -2), [-2,1), [1, 3), [3, 5]. 典例精析例2.证明:函数 在 上是增函数.证明:在区间 上任取两个值 且 ,且所以函数 在区间上 是增函数. 思考:如何证明一个函数是单调递增的呢?取值变形作差定号判断小试牛刀1.证明函数 在 是减函数 2.证明函数
在 上是增函数.3.证明函数 在 上是减函数四、归纳小结 3.函数单调性的证明,证明一般分五步:
取 值 → 作 差 → 化简 → 判号 → 下结论
2.会利用函数图像找出函数的单调区间1.函数单调性的定义看图结语:结论1:一次函数 的单调性,单调区间:结论2:二次函数
的单调性,单调区间:看图结语结论3:反比例函数
的单调性,单调区间: 你可以解答了:数学语言来刻画“随着时间的推移气温逐渐升高”这一特征?艾宾浩斯遗忘曲线单调性曲线升降成单调,
横向范围区间瞧。
一取二减三定号,
因式分解不可少。
牢记区间不能并,
任意取值才成立。
同增同减真君子,
此消彼长亦逍遥!
亦逍遥!
教学重点与难点??
? 1.从形与数两方面理解函数单调性的概念,初步掌握利用函数图象和单调性定义判断、证明函数单调性的方法.
2.通过对函数单调性定义的探究,渗透数形结合数学思想方法,培养学生观察、归纳、抽象的能力和语言表达能力;通过对函数单调性的证明,提高学生的推理论证能力.
3.通过知识的探究过程培养学生细心观察、认真分析、严谨论证的良好思维习惯,让学生经历从具体到抽象,从特殊到一般,从感性到理性的认知过程.【教学目标】【教学重点】?函数单调性的概念、判断及证明.
【教学难点】?归纳抽象函数单调性的定义以及根据定义证明函数的单调性.怎样用数学语言来刻画“随着时间的推移气温逐渐升高”这一特征?xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?蒸蒸日上xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?f(x1)x1xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?x1f(x1)xyy = xO11··实例分析:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?x1f(x1)xyy = xO11··实例1:画出函数y = x的图象观察函数图象,并指出函数的变化趋势?x1f(x1)xyy = xO11··x1f(x1)实例1:画出函数y = x的图象xyy = xO11··x1f(x1)1.从左至右图象上升还是下降 ____?
2.在区间 ________上,随着x的增大,f(x)的值随着 ______ .上升(-∞, +∞)增大实例2:画出函数 图像(反比例函数)每况愈下Oxy实例3:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象观察函数图象,并指出函数的变化趋势?Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象Oxy实例2:分析二次函数的图象1.在区间_______上,f(x)的值随着x的增大而_____.
2. 在区间_______上,f(x)的值随着x的增大而 _____. (-∞, 0](0, +∞)增大减小xyO此起彼伏看图结语 不同的函数,其图像的变化趋势可能不同,同一函数在不同的区间上变化趋势也不一定相同,函数的这种变化规律反映了函数的一个重要性质,即函数的单调性。函数单调性定义 一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1
数:x不断增大,y也不断增大共同进退→ 一般地,设函数y=f(x)的定义域为I,如果对于定义域I内的某个区间D内的任意两个自变量x1,x2,当x1
比如某个函数单调增区间为(2,5)和(7,9),必须写成(2,5)和(7,9),或(2,5),(7,9)。注意:例1.下图是定义在区间[-5,5]上的函数y=f(x),根据图象说出函数的单调区间,以及在每个区间上,它是增函数还是减函数?解:函数y=f(x)的单调区间有其中y=f(x)在区间[-5, -2), [1, 3)上是减函数,
在区间[-2, 1), [3, 5] 上是增函数.[-5, -2), [-2,1), [1, 3), [3, 5]. 典例精析例2.证明:函数 在 上是增函数.证明:在区间 上任取两个值 且 ,且所以函数 在区间上 是增函数. 思考:如何证明一个函数是单调递增的呢?取值变形作差定号判断小试牛刀1.证明函数 在 是减函数 2.证明函数
在 上是增函数.3.证明函数 在 上是减函数四、归纳小结 3.函数单调性的证明,证明一般分五步:
取 值 → 作 差 → 化简 → 判号 → 下结论
2.会利用函数图像找出函数的单调区间1.函数单调性的定义看图结语:结论1:一次函数 的单调性,单调区间:结论2:二次函数
的单调性,单调区间:看图结语结论3:反比例函数
的单调性,单调区间: 你可以解答了:数学语言来刻画“随着时间的推移气温逐渐升高”这一特征?艾宾浩斯遗忘曲线单调性曲线升降成单调,
横向范围区间瞧。
一取二减三定号,
因式分解不可少。
牢记区间不能并,
任意取值才成立。
同增同减真君子,
此消彼长亦逍遥!
亦逍遥!
