3.2.2 对数函数 课件 22张PPT
文档属性
| 名称 | 3.2.2 对数函数 课件 22张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 359.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 20:58:33 | ||
图片预览




文档简介
课件22张PPT。对数函数其中a叫做对数的底数,N叫做真数。一般地,如果 的b次幂等于N, 就是 ,那么数 b叫做以a为底 N的对数,记作
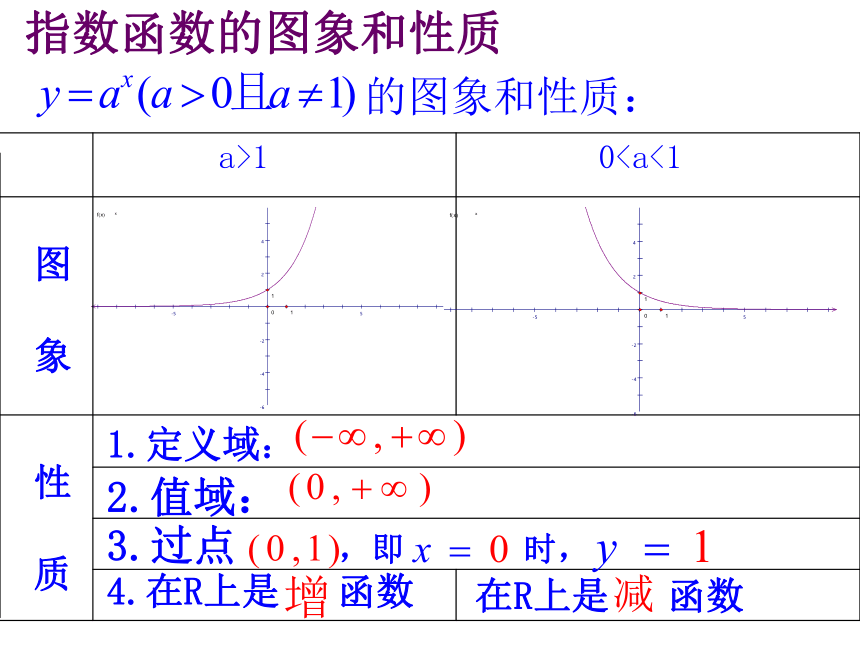
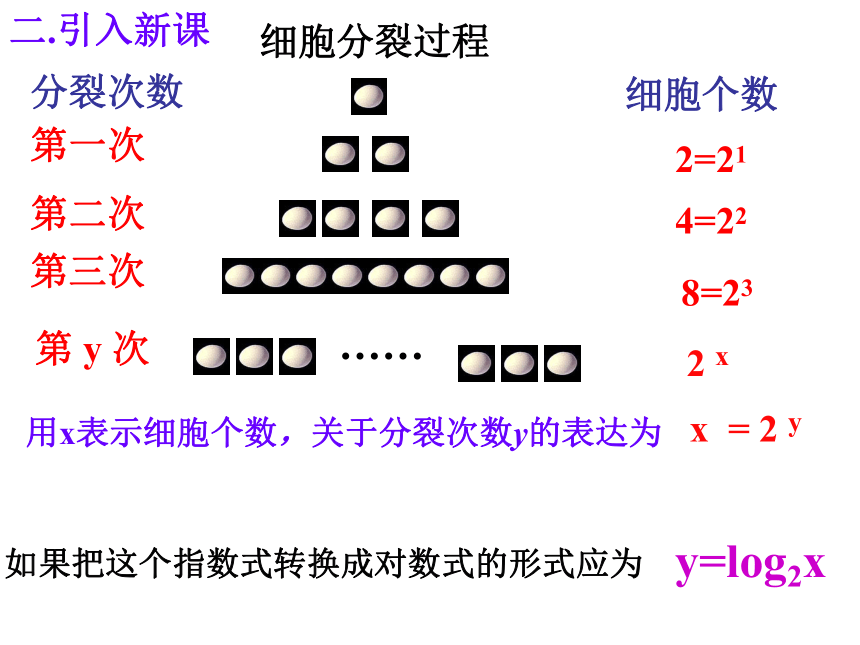
定义:(一)对数的概念底数对数真数幂指数底数的图象和性质: 指数函数的图象和性质二.引入新课细胞分裂过程细胞个数第一次第二次第三次2=218=234=22第 y 次……用x表示细胞个数,关于分裂次数y的表达为x = 2 y
2 x如果把这个指数式转换成对数式的形式应为y=log2x 分裂次数8=23(一)对数函数的定义★ 函数 y = log a x (a>0,a≠1)叫做对数函数. 其中x是自变量,定义域是(0,+∞)
描点法作图的基本步骤:(二)作y=log2x和y=log0.5x图象 一、列表(根据给定的自变量分别
计算出因变量的值)
二、描点(根据列表中的坐标分别在
坐标系中标出其对应点)
三、连线(将所描的点用平滑的曲线
连接起来)
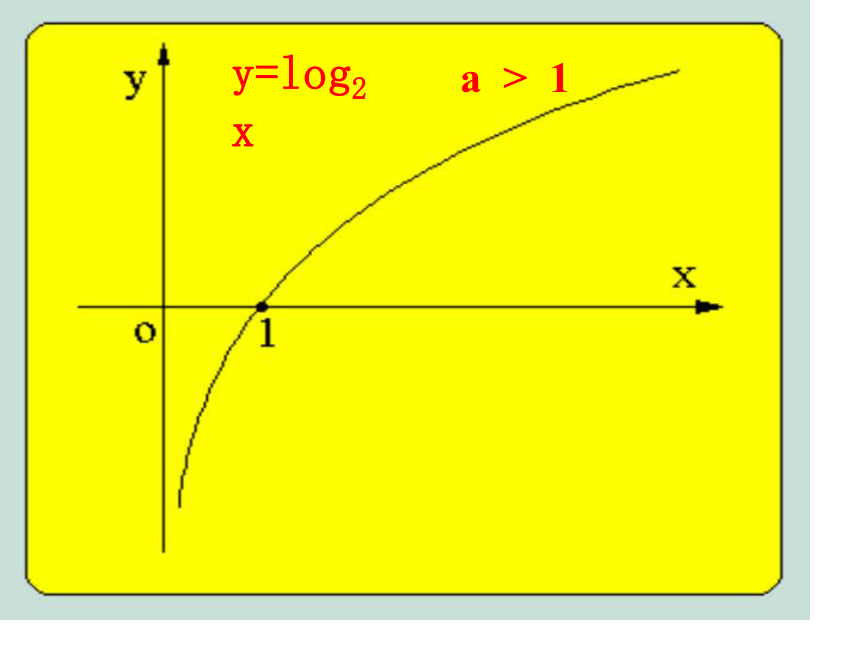
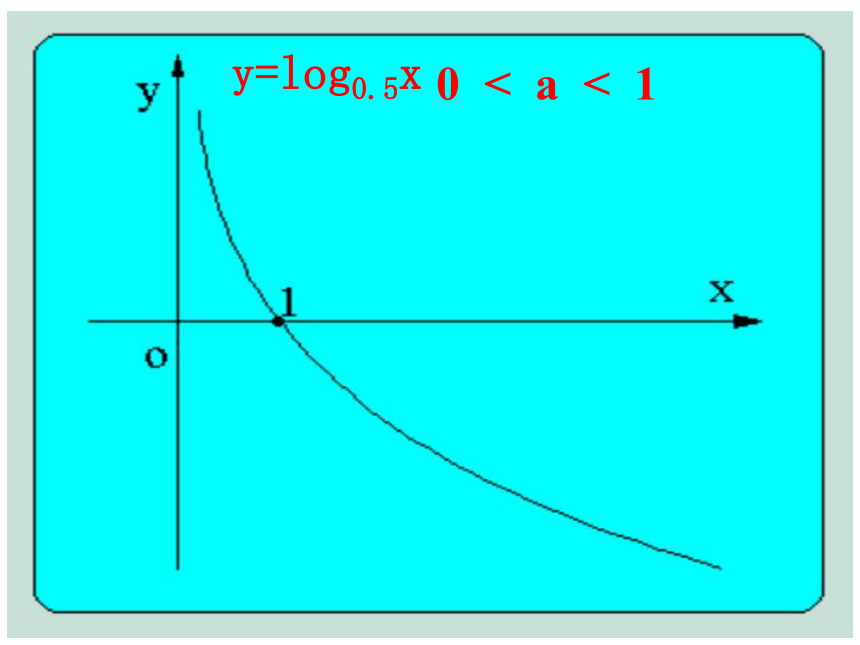
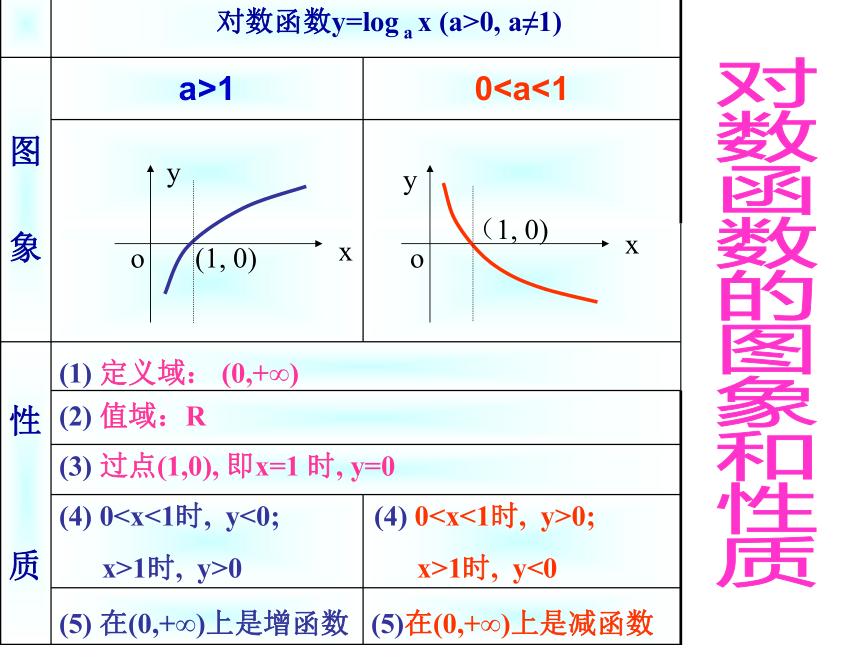
a > 1y=log2xy=log0.5x0 < a < 1对数函数y=log a x (a>0, a≠1)(4) 0 x>1时, y>0(4) 00;
x>1时, y<0 (3) 过点(1,0), 即x=1 时, y=0 (1) 定义域: (0,+∞)(2) 值域:Rxyo(1, 0)xyo(1, 0)(5)在(0,+∞)上是减函数(5) 在(0,+∞)上是增函数对数函数的图象和性质【练习】 画出函数的图象, ,并且说明这两个函数的相同性质和不同性质.解:相同性质: 不同性质: 两图象都位于的图象是上升的曲线,在(0,+∞)上是增函数; 的图象是下降的曲线,在(0,+∞) 上是减函数.y轴右方,都经过点(1,0),
这说明两函数的定义域都是【例1】求下列函数的定义域:解: 解:(1) 由 得∴函数 的定义域是(2) 由 得 ∴函数 的定义域是(3)求解对数函数定义域问题的关键是要
求真数大于零,当真数为某一代数式
时,可将其看作一个整体单独提出来,
求其大于零的解集,即该函数的定义域.
例题讲解例2:比较下列各组中,两个值的大小:
(1) log23与 log28.5 (2) log 0.7 1.6与 log 0.7 1.8 log23log28.5解法1:画图找点比高低解法2:利用对数函数的单调性考察函数y=log 2 x ,∵a=2 > 1,∴ y=log 2 x在(0,+∞)
上是增函数;∵3<8.5∴ log23< log28.5 ∴ log23< log28.5 例题讲解例2:比较下列各组中,两个值的大小:
(1) log23与 log28.5 (2) log 0.7 1.6与 log 0.7 1.8 解2:考察函数y=log 0.7 x ,
∵a=0.7< 1,
∴ y=log 0.7 x在区间(0,+∞)上是减函数;
∵1.6<1.8
∴ log 0.7 1.6> log 0.7 1.8 3.根据单调性得出结果。例2:比较下列各组中,两个值的大小:
(1) log23与 log28.5 (2) log 0.7 1.6与 log 0.7 1.8 1.观察底数是大于1还是小于1( a>1时为增函数
0即0 1例2:比较下列各组中,两个值的大小:
(3) loga5.1与 loga5.9解: 若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
若0 ∵5.1<5.9
∴ loga5.1 > loga5.9你能口答吗?变一变还能口答吗?<>><<<<<解:(4) 解:(3)要比较两个数的大小,一般首先考虑用函数单调性,如不能用,则可先观察其正负,其次观察其与1的大小关系。
想一想? (一)你能比较log34和log43的大小吗?提示:利用画图找点比高低的方法
在同一坐标内画出函数 y= log3x和y= log4x的图象你还能发现什么?0.1 底数a>1时,底数越大,其图象越接近x轴。补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形1 底数0
定义:(一)对数的概念底数对数真数幂指数底数的图象和性质: 指数函数的图象和性质二.引入新课细胞分裂过程细胞个数第一次第二次第三次2=218=234=22第 y 次……用x表示细胞个数,关于分裂次数y的表达为x = 2 y
2 x如果把这个指数式转换成对数式的形式应为y=log2x 分裂次数8=23(一)对数函数的定义★ 函数 y = log a x (a>0,a≠1)叫做对数函数. 其中x是自变量,定义域是(0,+∞)
描点法作图的基本步骤:(二)作y=log2x和y=log0.5x图象 一、列表(根据给定的自变量分别
计算出因变量的值)
二、描点(根据列表中的坐标分别在
坐标系中标出其对应点)
三、连线(将所描的点用平滑的曲线
连接起来)
a > 1y=log2xy=log0.5x0 < a < 1对数函数y=log a x (a>0, a≠1)(4) 0
x>1时, y<0 (3) 过点(1,0), 即x=1 时, y=0 (1) 定义域: (0,+∞)(2) 值域:Rxyo(1, 0)xyo(1, 0)(5)在(0,+∞)上是减函数(5) 在(0,+∞)上是增函数对数函数的图象和性质【练习】 画出函数的图象, ,并且说明这两个函数的相同性质和不同性质.解:相同性质: 不同性质: 两图象都位于的图象是上升的曲线,在(0,+∞)上是增函数; 的图象是下降的曲线,在(0,+∞) 上是减函数.y轴右方,都经过点(1,0),
这说明两函数的定义域都是【例1】求下列函数的定义域:解: 解:(1) 由 得∴函数 的定义域是(2) 由 得 ∴函数 的定义域是(3)求解对数函数定义域问题的关键是要
求真数大于零,当真数为某一代数式
时,可将其看作一个整体单独提出来,
求其大于零的解集,即该函数的定义域.
例题讲解例2:比较下列各组中,两个值的大小:
(1) log23与 log28.5 (2) log 0.7 1.6与 log 0.7 1.8 log23log28.5解法1:画图找点比高低解法2:利用对数函数的单调性考察函数y=log 2 x ,∵a=2 > 1,∴ y=log 2 x在(0,+∞)
上是增函数;∵3<8.5∴ log23< log28.5 ∴ log23< log28.5 例题讲解例2:比较下列各组中,两个值的大小:
(1) log23与 log28.5 (2) log 0.7 1.6与 log 0.7 1.8 解2:考察函数y=log 0.7 x ,
∵a=0.7< 1,
∴ y=log 0.7 x在区间(0,+∞)上是减函数;
∵1.6<1.8
∴ log 0.7 1.6> log 0.7 1.8 3.根据单调性得出结果。例2:比较下列各组中,两个值的大小:
(1) log23与 log28.5 (2) log 0.7 1.6与 log 0.7 1.8 1.观察底数是大于1还是小于1( a>1时为增函数
0
(3) loga5.1与 loga5.9解: 若a>1则函数在区间(0,+∞)上是增函数;
∵5.1<5.9
∴ loga5.1 < loga5.9
若0
∴ loga5.1 > loga5.9你能口答吗?变一变还能口答吗?<>><<<<<解:(4) 解:(3)要比较两个数的大小,一般首先考虑用函数单调性,如不能用,则可先观察其正负,其次观察其与1的大小关系。
想一想? (一)你能比较log34和log43的大小吗?提示:利用画图找点比高低的方法
在同一坐标内画出函数 y= log3x和y= log4x的图象你还能发现什么?0.1 底数a>1时,底数越大,其图象越接近x轴。补充性质二 底数互为倒数的两个对数函数的图象关于x轴对称。补充性质一
图
形1 底数0
