1.2.1 平面的基本性质 课件 56张PPT
文档属性
| 名称 | 1.2.1 平面的基本性质 课件 56张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 870.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 21:16:13 | ||
图片预览






文档简介
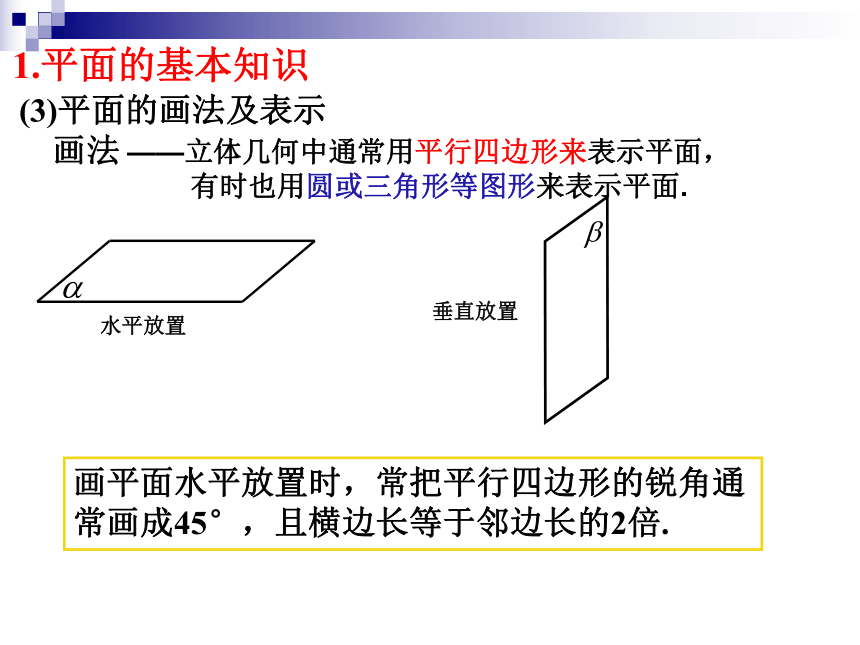
课件56张PPT。2.1 空间点、直线、平面之间的位置关系2.1.1 平面观察长方体,你能发现长方体的顶点、棱所在的直线,以及侧面、地面之间的关系吗?长方体由上下、前后、左右六个面围成,有些面是平行的,有些面是相交的;有些棱所在的直线与面平行,有些棱所在的直线与面相交;每条棱所在的直线都可以看作是某个面内的直线等等.空间中的点、直线、平面之间有什么位置关系,是我们接下来要讨论的问题.1.平面的基本知识(1)平面与我们学过的点、直线、集合等概念一样都是最基本的概念,即为不加定义的原始概念.(2)平面的基本特征是无限延展性.平面是理想的,绝对的平(平面是处处平直的面);
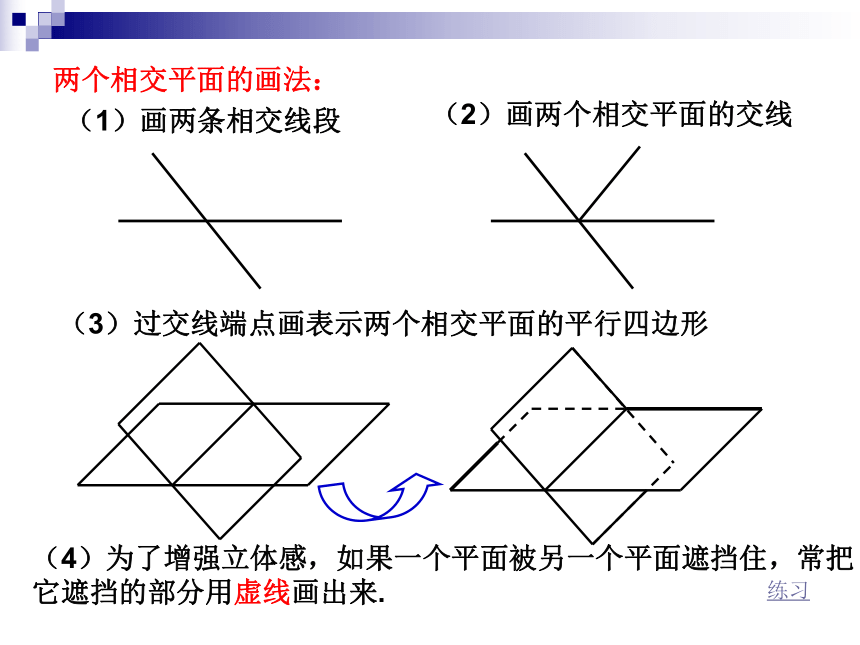
平面没有大小、没有厚薄和宽窄,是不可度量的.光滑的桌面、平静的湖面等都是我们熟悉的平面形象,数学中的平面概念是现实平面加以抽象的结果.思考:能不能说一个平面长4米,宽2米?为什么?不能.练习画法——立体几何中通常用平行四边形来表示平面, 有时也用圆或三角形等图形来表示平面.画平面水平放置时,常把平行四边形的锐角通常画成45°,且横边长等于邻边长的2倍.水平放置垂直放置(3)平面的画法及表示1.平面的基本知识(4)为了增强立体感,如果一个平面被另一个平面遮挡住,常把它遮挡的部分用虚线画出来.两个相交平面的画法:(1)画两条相交线段(2)画两个相交平面的交线(3)过交线端点画表示两个相交平面的平行四边形练习表示方法:ABCD②用表示平面的平行四边形的四个顶点的大写英文字母表示,
如平面ABCD.③用表示平面的平行四边形的相对的两个顶点的大写英文字母表示,如平面AC或者平面BD.(3)平面的画法及表示1.平面的基本知识(1)点、线、面的表示点(元素):大写字母A、B、C、D……
直线(点的集合):小写英文字母 或者两个大写英文字母
平面(点的集合):用希腊字母表示 ;
用平行四边形顶点字母或者其相对两字母表示.(2)点、线、面之间的位置关系的表示
用集合中的关系符号
元素与集合关系:
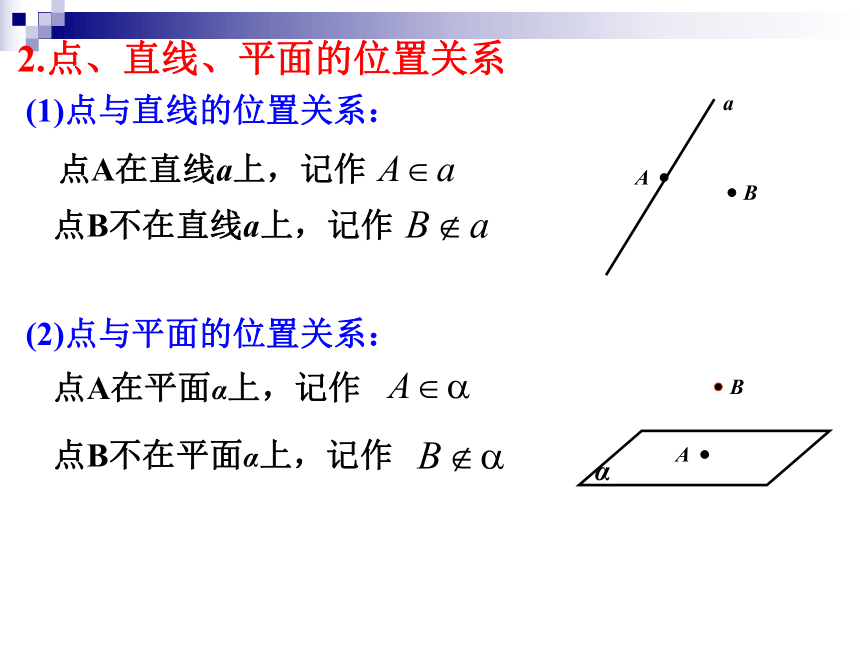
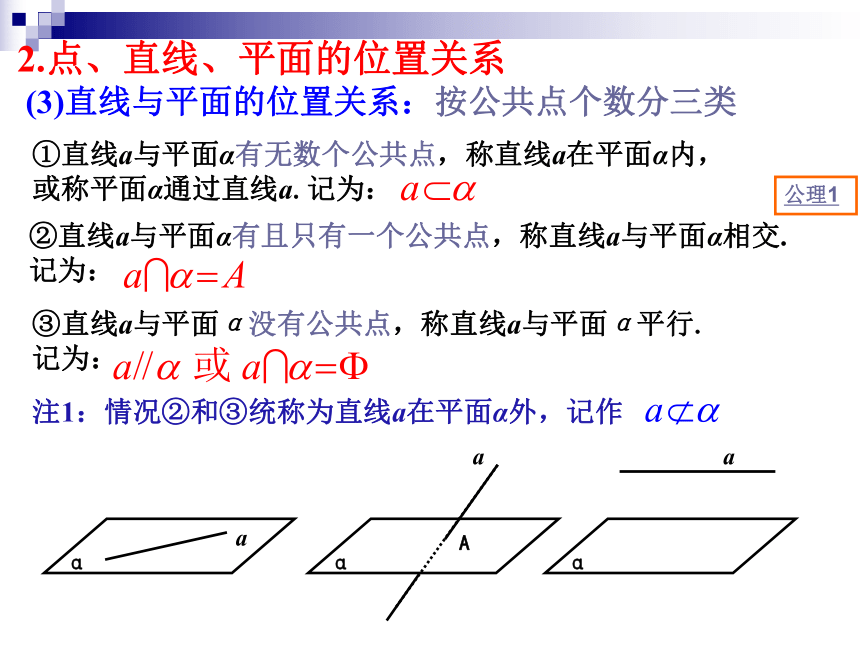
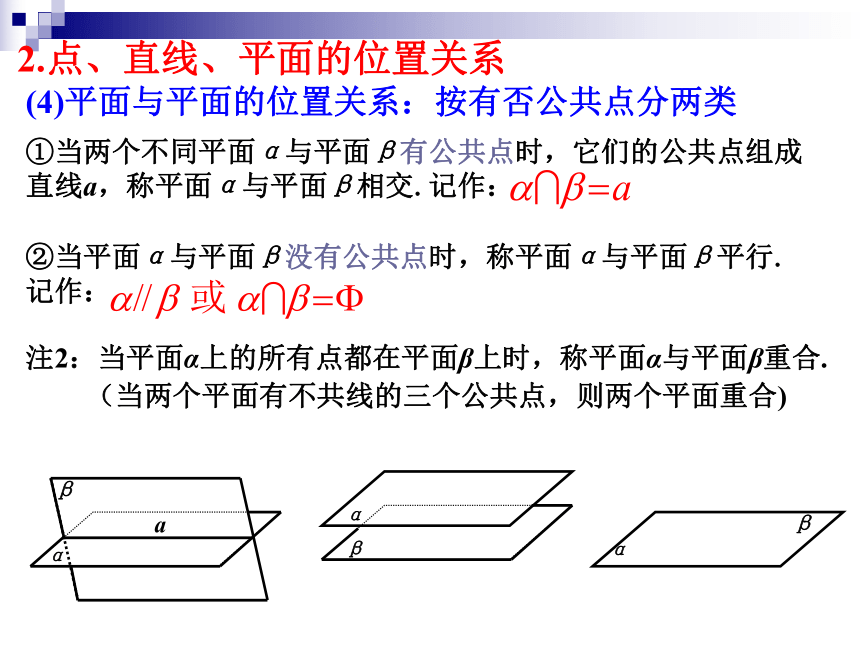
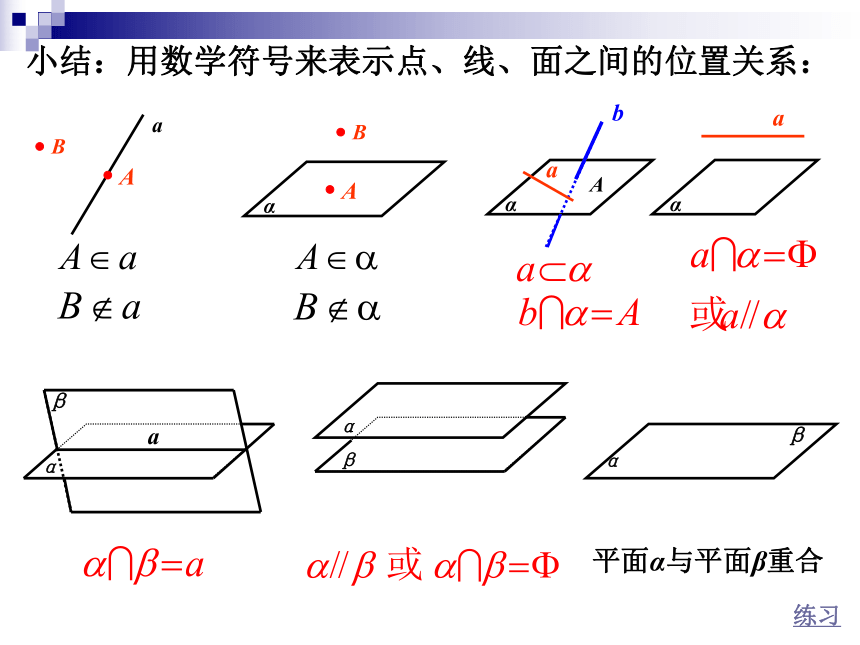
集合与集合关系:2.点、直线、平面的位置关系点A在直线a上,记作点B不在直线a上,记作点A在平面α上,记作点B不在平面α上,记作(1)点与直线的位置关系:(2)点与平面的位置关系:2.点、直线、平面的位置关系(3)直线与平面的位置关系:按公共点个数分三类②直线a与平面α有且只有一个公共点,称直线a与平面α相交. 记为:③直线a与平面α没有公共点,称直线a与平面α平行. 记为:①直线a与平面α有无数个公共点,称直线a在平面α内, 或称平面α通过直线a.记为:公理1注1:情况②和③统称为直线a在平面α外,记作2.点、直线、平面的位置关系(4)平面与平面的位置关系:按有否公共点分两类①当两个不同平面α与平面β有公共点时,它们的公共点组成直线a,称平面α与平面β相交.记作:②当平面α与平面β没有公共点时,称平面α与平面β平行.记作:注2:当平面α上的所有点都在平面β上时,称平面α与平面β重合.β(当两个平面有不共线的三个公共点,则两个平面重合)2.点、直线、平面的位置关系 例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.(1)(2)典型例题练习小结:用数学符号来表示点、线、面之间的位置关系:a练习β平面α与平面β重合观察下列问题,你能得到什么结论?直尺落在桌面上(直线AB在平面α内)3.平面的基本性质思考1:请你用尺子做实验并回答以下问题(分组讨论)
1. 如果一直线与一平面有一个公共点,那么这直线在平面内吗?
2. 如果一直线与一平面有两个公共点,那么这直线在平面内吗?①图形语言:(1)公理1:若一条直线上的两点在一个平面内, 则这条直线在此平面内.②符号语言:③该公理反映了直线与平面的位置关系: 可用于判定直线是否在平面内,点是否在平面内,又可用直线检验平面.3.平面的基本性质思考:两个平面会不会只有一个公共点呢?不会!因为平面是无限延展的.
因此,两个平面有一个公共点,必然有无数个公共点,并且这些公共点在一条直线上.3.平面的基本性质(2)公理3:若两个不重合的平面有一个公共点, 则它们有且只有一条过该点的公共直线.①图形语言:②符号语言:③该公理反映了平面与平面的位置关系:i)该公理是用以判定两个平面相交的依据:只要两个平面有一个公共点,就可判定这两个平面必相交于过该点的一条直线.
(找两个面的交线只要找出两个面的两个公共点即可)
ii)该公理可用以判定点在直线上:点是某两平面的公共点,线是这两个平面的公共交线,则该点在交线上.3.平面的基本性质观察下列问题,你能得到什么结论?自行车需要一个支脚架就可以保持平衡.3.平面的基本性质(3)公理2: 经过不在同一直线上的三点,有且只有一个平面.①图形语言:②符号语言:③定义的说明:
过不在一条直线上的四点,不一定有平面.故要充分重视“不在一条直线上的三点”这一条件;
“有且只有一个”强调的是存在性和唯一性两方面,不能用“只有一个”替代;
确定一个平面的“确定”是“有且只有”的同义词.3.平面的基本性质练习推论2 ?经过两条相交直线,有且只有一个平面.推论3 ?经过两条平行直线,有且只有一个平面.推论1 经过一条直线和这条直线外一点,有且只有一个平面.注3:
公理2及其三个推论是确定平面以及判断两个平面重合的依据,
是证明点、线共面的依据,也是作截面、辅助平面的依据.公理2: 经过不在同一直线上的三点,有且只有一个平面.练习3.平面的基本性质例3例2典例展示BCA返回【例3】如图,已知△ABC在平面α外,它的三边所在直线分别交平面α于点P、Q、R.
求证:P、Q、R三点共线.【证明】设△ABC 确定平面ABC,直线AB交平面α于点Q,直线CB交平面α于点P,直线AC交平面α于点R,则P、Q、R三点都在平面α内。又因为P、Q、R三点都在平面ABC内,所以P、Q、R三点都在平面α和平面ABC的交线上.
ABCPQR因为两平面的交线只有一条,所以P、Q、R三点共线.
返回一、基本知识平面基本性质平面无限延展平面的画法公理1公理2公理3概念平面的表示法判定线在面内的依据确定平面的条件判定点共线线共点的依据作业:《同步训练》2.1.1再见再
见
!立体几何我们知道,在同一平面内, 如果两条直线都和第三条直线平行,
那么这两条直线互相平行.在空间这一规律是否还成立呢?观察 : 将一张纸如图进行折叠 , 则各折痕及边 a, b, c, d, e, …
之间有何关系?a∥b ∥c ∥d ∥e ∥ …3.平面的基本性质符号表示:(4)公理4:平行于同一条直线的两条直线互相平行.①平行具有传递性;注4:②该公理是判断空间两条直线平行的方法之一.即要证明两条直线平行,一般利用第三条直线作为联系两直线的中间环节.3.平面的基本性质例1 在正方体ABCD—A1B1C1D1中,直线AB与C1D1 ,AD1与BC1是什么位置关系?为什么?解:1)∵AB∥A1B1, C1D1 ∥A1B1, ∴ AB ∥ C1D1 2)∵AB ∥C1D1 ,且AB = C1D1 ∴ ABC1D1为平行四边形故AD1 ∥ BC1 练习:上例中,AA1与CC1,AC与A1C1的位置是什么关系?例2 已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC,CD,DA的中点,连结EF,FG,GH,HE,求证:EFGH是一个平行四边形.问1:若上例加上条件AC=BD,则四边形EFGH是一个什么图形?“见中点找中点”构造三角形的中位线是证明平行的常用方法.∵ EH是△ABD的中位线,∴EH ∥FG且EH =FG.∴EFGH是一个平行四边形.证明:连结BD,菱形问2:若上例中四边形EFGH为矩形,AC与BD垂直吗?另注:平行线段成比例练习√√√OEF例 几何体中的截面问题(两平面的交线问题)Q即交线为QN例 几何体中的截面问题(两平面的交线问题)拓展4.点线共面问题(1)证明的主要依据:公理1;公理2及其三个推论.
(2)证明的常用方法:
①纳入平面法:先由部分元素确定一个平面,再证明其余有关的点、线在此平面内;
②辅助平面法:先证明有关的点、线确定平面?,再证明其余元素确定平面?,最后证明平面?、?重合.例1 证明两两相交且不同点的三条直线必在同一个平面内.已知:AB∩AC=A,AB∩BC=B,AC∩BC=C求证:直线AB,BC,AC共面.证明:因为AB∩AC=A,所以直线AB,AC确定一个平面?.(推论2)因为B∈AB,C∈AC,所以B∈?,C∈?,故BC??.(公理1)因此直线AB,BC,CA共面.确定一个面,再证明其余线在该面内.4.点线共面问题证法二:因为A? 直线BC上,所以过点A和直线BC确定平面? .(推论1)因为B∈BC,所以B∈? . 又A∈?, 故AB ??,同理AC ? ?,所以AB,AC,BC共面.例1 证明两两相交且不同点的三条直线必在同一个平面内.证法三:因为A,B,C三点不在一条直线上,所以过A,B,C三点可以确定平面?.(公理2)因为A∈?,B∈?,所以AB ? ?.(公理1)同理BC ? ?,AC ? ?,所以AB,BC,CA三直线共面.4.点线共面问题4.点线共面问题P51 5 证明:一条直线与两条平行直线都相交,则这三条直线共面.已知:a//b,a∩c=A,b∩c=B.求证:直线a,b,c共面.证明:因为a//b,所以直线a,b确定一个平面? .(推论3)因为A∈a,B∈b,所以A∈?,B∈?.又因为A∈c,B∈c.故AB?? .(公理1)因此直线a,b,c共面.4.点线共面问题例2 已知一条直线与三条平行直线都相交,证明这四条直线共面.已知:a//b//c,a∩l=A,b∩l=B, c∩l=C.求证:直线l与a,b,c共面.证明:∵a//b,∴直线a,b确定一个平面?.(推论3)∵ l ∩a=A, l ∩b=B,∴ A∈?,B∈?.又A∈l,B∈l,故l ??. 同理,直线b,c确定一个平面?,且l ?? .∴平面?与?都过两相交直线b,l.又∵两相交直线确定一个唯一的平面.
∴?与?重合.
故l与a,b,c共面.证明两个平面重合是证明直线在平面内问题的重要方法.4.点线共面问题练 已知a ??,b ??,a∩b=A,P∈b,PQ//a . 求证:PQ ?? .4.点线共面问题(1)证明的主要依据是公理3:
如果两个平面相交,则这两个平面的公共点共线;
如果两个平面相交,那么一个平面内的直线和另一平面的交点必在这两个平面的交线上.
(2)证明的常用方法:
①首先找出两个平面,再证这三个点都是这两个平面的公共点;
②选择其中两点确定一条直线,然后证明另一个点也在其上(一般地,这条直线看作某两个平面的交线,往证第三个点也是两个面的公共点);
③证明三线共点问题:先证明两条直线交于一个点,再证明第三条直线经过这个点(转化为证明点在线上的问题)5.证明三点共线、三线共点的问题例1 已知三角形ABC的三条边AB、BC、AC与平面α分别交于P、Q、R.求证:P、Q、R共线.BAQRCP证明:同理Q、R也为公共点,所以P、Q、R共线.要证明各点共线,只要证明他们是两个相交平面的公共点.5.证明三点共线、三线共点的问题P53 3 空间四边形ABCD中,E,F分别是AB和CB上的点,G,H分别是CD和AD上的点,且EH与FG相交于K.
求证:EH,BD,FG三条直线相交于同一点.分析:
已知EH∩FG=K,要证EH,BD,FG共点.
即要证明B,D,K三点共线.而BD是面ABD和面CBD的交线.
所以往证K∈面ABD∩面CBD.而显然,由EH∈面ABD,K∈EH,可得K∈面ABD.
同理,由FG∈面CBD,K∈FG,可得K∈面CBD.5.证明三点共线、三线共点的问题小结:空间点、线、面的位置关系
平面的基本性质(四个公理)
证明直线平行的常用方法
点线共面,三线共点,三点共线问题的证明作业:P51 5、6
P53 B组2、3
P78 3、4、8
精讲精练: P18 9、8“见中点找中点”构造三角形的中位线是证明平行的常用方法.P78 4,5G(2) 立体几何中求解平面的角度边长面积等问题时,注意重新画出图形,结合几何体找出边角关系并利用平面图形性质求解问题.back例 几何体中的截面问题(两平面的交线问题)精讲精练P2 4(正方体的截面形状的研究)back正方体截面形状小结例 几何体中的截面问题(两平面的交线问题)正方体中,试画出过其中三条棱的中点P,Q,R的平面截得正方体的截面形状.back正方体中,试画出过其中三条棱的中点P,Q,R的平面截得正方体的截面形状.S即交线为RS交AA1于中点GKGHST即交线为QT交CC1于中点HT例 几何体中的截面问题(两平面的交线问题)back例 几何体中的截面问题(两平面的交线问题)正方体中,试画出过其中三条棱的中点P,Q,R的平面截得正方体的截面形状.back*画出四面体ABCD中过E,F,G三点的截面与四面体各面的交线.P即交线为GPDH 即交线为FH例 几何体中的截面问题(两平面的交线问题)back一、判断下列各题的说法正确与否:
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是 4 cm 2; ( )
5、一个平面可以把空间分成两部分. ( )练习back画出两个竖直放置的相交平面.练习back(6)平面A1C1CA∩平面D1B1BD=OO1练习back2.根据下列符号表示的语句,说出有关点、线、面的关系,并画出图形.back练习(1)过一点可以做几条直线?两点呢?(2)过平面内一点可以做几个平面?两点呢?三点呢?思考:back(3)不共面的四点可以确定多少个平面?
(4)共点的三条直线可以确定多少个平面?4 个1个或3个3.填空:
_________________的三点确定一个平面;
两条 或 直线确定一个平面;
有一个公共点的两个平面交于 的一条直线.不在同一直线上平行相交唯一练习4.下列命题正确的是( ) A. 经过三点确定一个平面 B.经过一条直线和一个点确定一个平面 C.四边形确定一个平面 D.两两相交且不共点的三条直线确定一个平面Dback5.判断下列命题是否正确:
(1)平面α与平面β相交,它们只有有限个公共点.
(2)经过一条直线和这条直线外的一点,有且只有一个平面.
(3)经过两条相交直线,有且只有一个平面.
(4)如果两个平面有三个不共线的公共点,那么这两个平面重合.×√√√练习back
如平面ABCD.③用表示平面的平行四边形的相对的两个顶点的大写英文字母表示,如平面AC或者平面BD.(3)平面的画法及表示1.平面的基本知识(1)点、线、面的表示点(元素):大写字母A、B、C、D……
直线(点的集合):小写英文字母 或者两个大写英文字母
平面(点的集合):用希腊字母表示 ;
用平行四边形顶点字母或者其相对两字母表示.(2)点、线、面之间的位置关系的表示
用集合中的关系符号
元素与集合关系:
集合与集合关系:2.点、直线、平面的位置关系点A在直线a上,记作点B不在直线a上,记作点A在平面α上,记作点B不在平面α上,记作(1)点与直线的位置关系:(2)点与平面的位置关系:2.点、直线、平面的位置关系(3)直线与平面的位置关系:按公共点个数分三类②直线a与平面α有且只有一个公共点,称直线a与平面α相交. 记为:③直线a与平面α没有公共点,称直线a与平面α平行. 记为:①直线a与平面α有无数个公共点,称直线a在平面α内, 或称平面α通过直线a.记为:公理1注1:情况②和③统称为直线a在平面α外,记作2.点、直线、平面的位置关系(4)平面与平面的位置关系:按有否公共点分两类①当两个不同平面α与平面β有公共点时,它们的公共点组成直线a,称平面α与平面β相交.记作:②当平面α与平面β没有公共点时,称平面α与平面β平行.记作:注2:当平面α上的所有点都在平面β上时,称平面α与平面β重合.β(当两个平面有不共线的三个公共点,则两个平面重合)2.点、直线、平面的位置关系 例1 如图,用符号表示下列图形中点、直线、平面之间的位置关系.(1)(2)典型例题练习小结:用数学符号来表示点、线、面之间的位置关系:a练习β平面α与平面β重合观察下列问题,你能得到什么结论?直尺落在桌面上(直线AB在平面α内)3.平面的基本性质思考1:请你用尺子做实验并回答以下问题(分组讨论)
1. 如果一直线与一平面有一个公共点,那么这直线在平面内吗?
2. 如果一直线与一平面有两个公共点,那么这直线在平面内吗?①图形语言:(1)公理1:若一条直线上的两点在一个平面内, 则这条直线在此平面内.②符号语言:③该公理反映了直线与平面的位置关系: 可用于判定直线是否在平面内,点是否在平面内,又可用直线检验平面.3.平面的基本性质思考:两个平面会不会只有一个公共点呢?不会!因为平面是无限延展的.
因此,两个平面有一个公共点,必然有无数个公共点,并且这些公共点在一条直线上.3.平面的基本性质(2)公理3:若两个不重合的平面有一个公共点, 则它们有且只有一条过该点的公共直线.①图形语言:②符号语言:③该公理反映了平面与平面的位置关系:i)该公理是用以判定两个平面相交的依据:只要两个平面有一个公共点,就可判定这两个平面必相交于过该点的一条直线.
(找两个面的交线只要找出两个面的两个公共点即可)
ii)该公理可用以判定点在直线上:点是某两平面的公共点,线是这两个平面的公共交线,则该点在交线上.3.平面的基本性质观察下列问题,你能得到什么结论?自行车需要一个支脚架就可以保持平衡.3.平面的基本性质(3)公理2: 经过不在同一直线上的三点,有且只有一个平面.①图形语言:②符号语言:③定义的说明:
过不在一条直线上的四点,不一定有平面.故要充分重视“不在一条直线上的三点”这一条件;
“有且只有一个”强调的是存在性和唯一性两方面,不能用“只有一个”替代;
确定一个平面的“确定”是“有且只有”的同义词.3.平面的基本性质练习推论2 ?经过两条相交直线,有且只有一个平面.推论3 ?经过两条平行直线,有且只有一个平面.推论1 经过一条直线和这条直线外一点,有且只有一个平面.注3:
公理2及其三个推论是确定平面以及判断两个平面重合的依据,
是证明点、线共面的依据,也是作截面、辅助平面的依据.公理2: 经过不在同一直线上的三点,有且只有一个平面.练习3.平面的基本性质例3例2典例展示BCA返回【例3】如图,已知△ABC在平面α外,它的三边所在直线分别交平面α于点P、Q、R.
求证:P、Q、R三点共线.【证明】设△ABC 确定平面ABC,直线AB交平面α于点Q,直线CB交平面α于点P,直线AC交平面α于点R,则P、Q、R三点都在平面α内。又因为P、Q、R三点都在平面ABC内,所以P、Q、R三点都在平面α和平面ABC的交线上.
ABCPQR因为两平面的交线只有一条,所以P、Q、R三点共线.
返回一、基本知识平面基本性质平面无限延展平面的画法公理1公理2公理3概念平面的表示法判定线在面内的依据确定平面的条件判定点共线线共点的依据作业:《同步训练》2.1.1再见再
见
!立体几何我们知道,在同一平面内, 如果两条直线都和第三条直线平行,
那么这两条直线互相平行.在空间这一规律是否还成立呢?观察 : 将一张纸如图进行折叠 , 则各折痕及边 a, b, c, d, e, …
之间有何关系?a∥b ∥c ∥d ∥e ∥ …3.平面的基本性质符号表示:(4)公理4:平行于同一条直线的两条直线互相平行.①平行具有传递性;注4:②该公理是判断空间两条直线平行的方法之一.即要证明两条直线平行,一般利用第三条直线作为联系两直线的中间环节.3.平面的基本性质例1 在正方体ABCD—A1B1C1D1中,直线AB与C1D1 ,AD1与BC1是什么位置关系?为什么?解:1)∵AB∥A1B1, C1D1 ∥A1B1, ∴ AB ∥ C1D1 2)∵AB ∥C1D1 ,且AB = C1D1 ∴ ABC1D1为平行四边形故AD1 ∥ BC1 练习:上例中,AA1与CC1,AC与A1C1的位置是什么关系?例2 已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC,CD,DA的中点,连结EF,FG,GH,HE,求证:EFGH是一个平行四边形.问1:若上例加上条件AC=BD,则四边形EFGH是一个什么图形?“见中点找中点”构造三角形的中位线是证明平行的常用方法.∵ EH是△ABD的中位线,∴EH ∥FG且EH =FG.∴EFGH是一个平行四边形.证明:连结BD,菱形问2:若上例中四边形EFGH为矩形,AC与BD垂直吗?另注:平行线段成比例练习√√√OEF例 几何体中的截面问题(两平面的交线问题)Q即交线为QN例 几何体中的截面问题(两平面的交线问题)拓展4.点线共面问题(1)证明的主要依据:公理1;公理2及其三个推论.
(2)证明的常用方法:
①纳入平面法:先由部分元素确定一个平面,再证明其余有关的点、线在此平面内;
②辅助平面法:先证明有关的点、线确定平面?,再证明其余元素确定平面?,最后证明平面?、?重合.例1 证明两两相交且不同点的三条直线必在同一个平面内.已知:AB∩AC=A,AB∩BC=B,AC∩BC=C求证:直线AB,BC,AC共面.证明:因为AB∩AC=A,所以直线AB,AC确定一个平面?.(推论2)因为B∈AB,C∈AC,所以B∈?,C∈?,故BC??.(公理1)因此直线AB,BC,CA共面.确定一个面,再证明其余线在该面内.4.点线共面问题证法二:因为A? 直线BC上,所以过点A和直线BC确定平面? .(推论1)因为B∈BC,所以B∈? . 又A∈?, 故AB ??,同理AC ? ?,所以AB,AC,BC共面.例1 证明两两相交且不同点的三条直线必在同一个平面内.证法三:因为A,B,C三点不在一条直线上,所以过A,B,C三点可以确定平面?.(公理2)因为A∈?,B∈?,所以AB ? ?.(公理1)同理BC ? ?,AC ? ?,所以AB,BC,CA三直线共面.4.点线共面问题4.点线共面问题P51 5 证明:一条直线与两条平行直线都相交,则这三条直线共面.已知:a//b,a∩c=A,b∩c=B.求证:直线a,b,c共面.证明:因为a//b,所以直线a,b确定一个平面? .(推论3)因为A∈a,B∈b,所以A∈?,B∈?.又因为A∈c,B∈c.故AB?? .(公理1)因此直线a,b,c共面.4.点线共面问题例2 已知一条直线与三条平行直线都相交,证明这四条直线共面.已知:a//b//c,a∩l=A,b∩l=B, c∩l=C.求证:直线l与a,b,c共面.证明:∵a//b,∴直线a,b确定一个平面?.(推论3)∵ l ∩a=A, l ∩b=B,∴ A∈?,B∈?.又A∈l,B∈l,故l ??. 同理,直线b,c确定一个平面?,且l ?? .∴平面?与?都过两相交直线b,l.又∵两相交直线确定一个唯一的平面.
∴?与?重合.
故l与a,b,c共面.证明两个平面重合是证明直线在平面内问题的重要方法.4.点线共面问题练 已知a ??,b ??,a∩b=A,P∈b,PQ//a . 求证:PQ ?? .4.点线共面问题(1)证明的主要依据是公理3:
如果两个平面相交,则这两个平面的公共点共线;
如果两个平面相交,那么一个平面内的直线和另一平面的交点必在这两个平面的交线上.
(2)证明的常用方法:
①首先找出两个平面,再证这三个点都是这两个平面的公共点;
②选择其中两点确定一条直线,然后证明另一个点也在其上(一般地,这条直线看作某两个平面的交线,往证第三个点也是两个面的公共点);
③证明三线共点问题:先证明两条直线交于一个点,再证明第三条直线经过这个点(转化为证明点在线上的问题)5.证明三点共线、三线共点的问题例1 已知三角形ABC的三条边AB、BC、AC与平面α分别交于P、Q、R.求证:P、Q、R共线.BAQRCP证明:同理Q、R也为公共点,所以P、Q、R共线.要证明各点共线,只要证明他们是两个相交平面的公共点.5.证明三点共线、三线共点的问题P53 3 空间四边形ABCD中,E,F分别是AB和CB上的点,G,H分别是CD和AD上的点,且EH与FG相交于K.
求证:EH,BD,FG三条直线相交于同一点.分析:
已知EH∩FG=K,要证EH,BD,FG共点.
即要证明B,D,K三点共线.而BD是面ABD和面CBD的交线.
所以往证K∈面ABD∩面CBD.而显然,由EH∈面ABD,K∈EH,可得K∈面ABD.
同理,由FG∈面CBD,K∈FG,可得K∈面CBD.5.证明三点共线、三线共点的问题小结:空间点、线、面的位置关系
平面的基本性质(四个公理)
证明直线平行的常用方法
点线共面,三线共点,三点共线问题的证明作业:P51 5、6
P53 B组2、3
P78 3、4、8
精讲精练: P18 9、8“见中点找中点”构造三角形的中位线是证明平行的常用方法.P78 4,5G(2) 立体几何中求解平面的角度边长面积等问题时,注意重新画出图形,结合几何体找出边角关系并利用平面图形性质求解问题.back例 几何体中的截面问题(两平面的交线问题)精讲精练P2 4(正方体的截面形状的研究)back正方体截面形状小结例 几何体中的截面问题(两平面的交线问题)正方体中,试画出过其中三条棱的中点P,Q,R的平面截得正方体的截面形状.back正方体中,试画出过其中三条棱的中点P,Q,R的平面截得正方体的截面形状.S即交线为RS交AA1于中点GKGHST即交线为QT交CC1于中点HT例 几何体中的截面问题(两平面的交线问题)back例 几何体中的截面问题(两平面的交线问题)正方体中,试画出过其中三条棱的中点P,Q,R的平面截得正方体的截面形状.back*画出四面体ABCD中过E,F,G三点的截面与四面体各面的交线.P即交线为GPDH 即交线为FH例 几何体中的截面问题(两平面的交线问题)back一、判断下列各题的说法正确与否:
1、一个平面长 4 米,宽 2 米; ( )
2、平面有边界; ( )
3、一个平面的面积是 25 cm 2; ( )
4、菱形的面积是 4 cm 2; ( )
5、一个平面可以把空间分成两部分. ( )练习back画出两个竖直放置的相交平面.练习back(6)平面A1C1CA∩平面D1B1BD=OO1练习back2.根据下列符号表示的语句,说出有关点、线、面的关系,并画出图形.back练习(1)过一点可以做几条直线?两点呢?(2)过平面内一点可以做几个平面?两点呢?三点呢?思考:back(3)不共面的四点可以确定多少个平面?
(4)共点的三条直线可以确定多少个平面?4 个1个或3个3.填空:
_________________的三点确定一个平面;
两条 或 直线确定一个平面;
有一个公共点的两个平面交于 的一条直线.不在同一直线上平行相交唯一练习4.下列命题正确的是( ) A. 经过三点确定一个平面 B.经过一条直线和一个点确定一个平面 C.四边形确定一个平面 D.两两相交且不共点的三条直线确定一个平面Dback5.判断下列命题是否正确:
(1)平面α与平面β相交,它们只有有限个公共点.
(2)经过一条直线和这条直线外的一点,有且只有一个平面.
(3)经过两条相交直线,有且只有一个平面.
(4)如果两个平面有三个不共线的公共点,那么这两个平面重合.×√√√练习back
