1.2.3 直线与平面的位置关系 课件 23张PPT
文档属性
| 名称 | 1.2.3 直线与平面的位置关系 课件 23张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 101.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 21:23:30 | ||
图片预览





文档简介
课件23张PPT。 苏教版 高中数学 高一上
直线与平面的位置关系
直线和平面平行
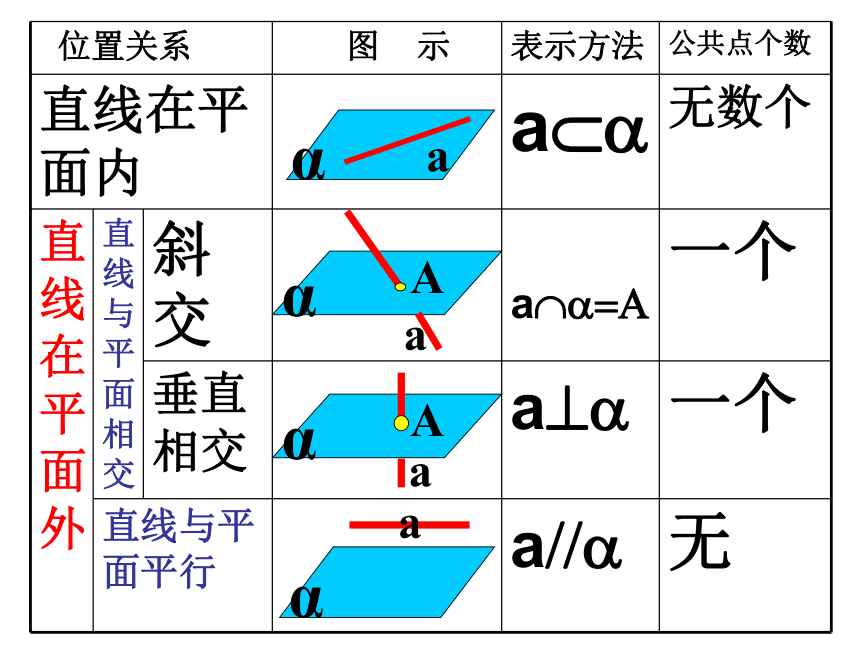
直线在平面直线和平面相交直线和平面平行线面位置关系有无数个公共点有且仅有一个公共点没有公共点αaαaαAAaαa线面平行的判定(1) 定义——直线与平面没有公共点 (2)线面平行判定定理
如果平面外一条直线和这个平面内的一直线平行,那么这条直线和这个平面平行。
(3)线面平行的性质
如果一条直线与一个平面平行,
经过这条直线的平面和这个平面相交,
则这条直线与交线平行。
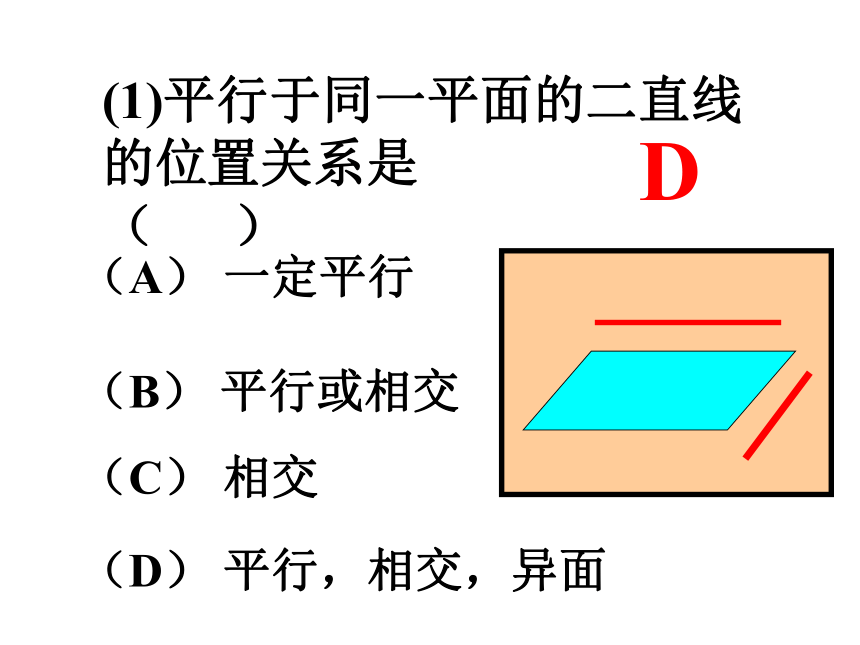
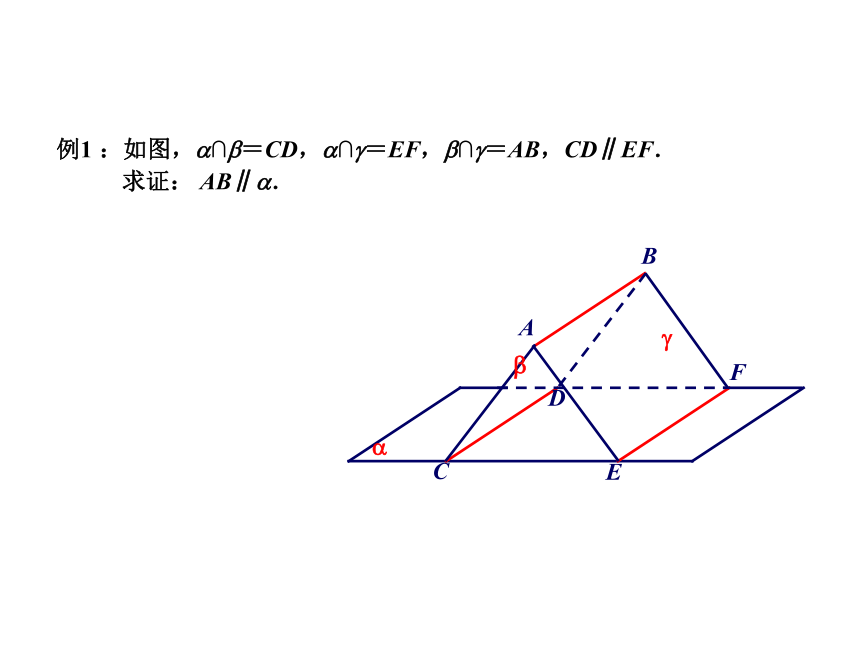
(1)平行于同一平面的二直线的位置关系是 ( )(A) 一定平行(B) 平行或相交(C) 相交(D) 平行,相交,异面D(2)如果l1 // l2 , l1 平行于平面?, 则l2 平面?l1?? 或 //例1 :如图,?∩?=CD,?∩?=EF,?∩?=AB,CD∥EF.
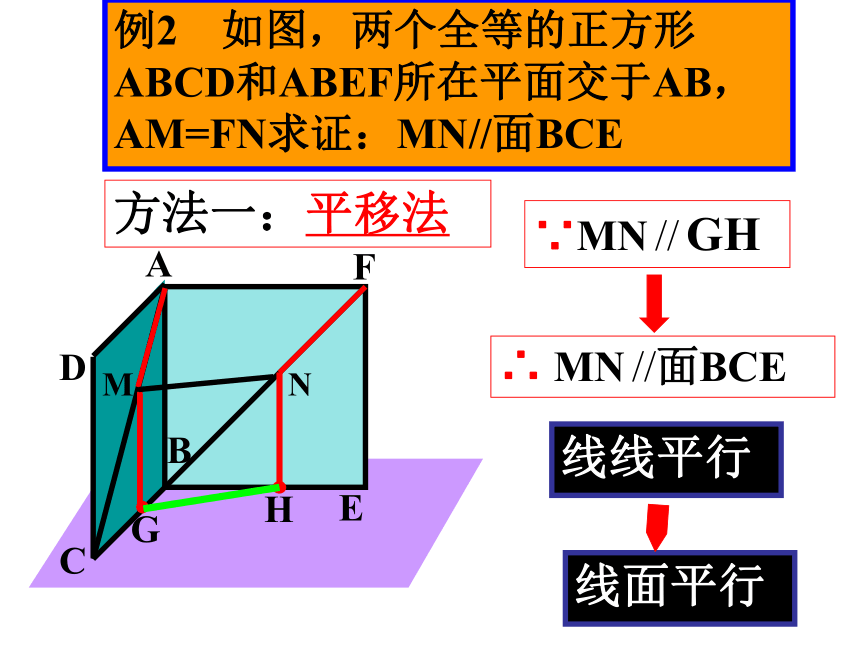
求证: AB∥?. ??例2 如图,两个全等的正方形ABCD和ABEF所在平面交于AB,AM=FN求证:MN//面BCEABCDEFMN∵MN // GH∴ MN //面BCE线线平行线面平行方法一:平移法例2 如图,两个全等的正方形ABCD和ABEF所在平面交于AB,AM=FN求证:MN//面BCEABCDEFMN∵△AFN∽ △HNB∴ AN/NH=FN/BN∴ AN/NH=AM/MC∴ MN//CH∴ MN //面BCE方法二:截面法例2 如图,两个全等的正方形ABCD和ABEF所在平面交于AB,AM=FN求证:MN//面BCEABCDEFMN方法三:面面平行G作MG//BC
则AM/MC=AG/GB
又AM/MC=FN/NB
则GN/AF直线与平面平行证明常用方法: 主要用在 ____________情况下 平行、垂直较多 方法好想,书写较繁,一般不能给第二小问提示,最好用截面法.
②截面法:③面面平行:①平移法 :两条相交直线___________确定,线面平行转化为线线平行。截面由常用辅助线:见中点,想中位线
例3 在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1EE∵DB1 // EF∴ DB1 //面A1C1E线线平行线面平行方法一:截面法12例3 在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1EE方法二:面面平行F练习1.如图,在四棱锥P-ABCD中,M,N分别是AB,PC的中点,若ABCD是平行四边形,求证:MN∥平面PAD.PABCDMNQQ练习2.在正方体AC1中,O为平面ADD1A1的中心, 求证:CO // 面A1C1BB1O方法一:截面法练习2.在正方体AC1中,O为平面ADD1A1的中心, 求证:CO // 面A1C1BB1O方法二:面面平行练习3、在直三棱柱ABC—A1B1C1,D是AB中点,求证:AC1∥面B1CDBAA1CADB1C1O方法一:截面法练习3、在直三棱柱ABC—A1B1C1,D是AB中点,求证:AC1∥面B1CDBAA1CADB1C1O方法二:面面平行E六、小结1,直线与平面平行判定定理与性质定理
(1)判定定理:
(2)性质定理
2、直线与平面平行证明常用方法:
①平移法 :
②截面法:
③面面平行:
3,常用辅助线:见中点,想中位线
作业作业:用三种方法证明。如图,M,N分别是正方体ABCD—A1B1C1D1的棱、AA1 , CD1 中点
求证:MN∥面ABCD。MNE方法一:平移法 练习4、如图,M,N分别是正方体ABCD—A1B1C1D1的棱、AA1 , CD1 中点
求证:MN∥面ABCD。MNE方法二:截面法P练习4、如图,M,N分别是正方体ABCD—A1B1C1D1的棱、AA1 , CD1 中点
求证:MN∥面ABCD。MNE方法三:面面平行
直线与平面的位置关系
直线和平面平行
直线在平面直线和平面相交直线和平面平行线面位置关系有无数个公共点有且仅有一个公共点没有公共点αaαaαAAaαa线面平行的判定(1) 定义——直线与平面没有公共点 (2)线面平行判定定理
如果平面外一条直线和这个平面内的一直线平行,那么这条直线和这个平面平行。
(3)线面平行的性质
如果一条直线与一个平面平行,
经过这条直线的平面和这个平面相交,
则这条直线与交线平行。
(1)平行于同一平面的二直线的位置关系是 ( )(A) 一定平行(B) 平行或相交(C) 相交(D) 平行,相交,异面D(2)如果l1 // l2 , l1 平行于平面?, 则l2 平面?l1?? 或 //例1 :如图,?∩?=CD,?∩?=EF,?∩?=AB,CD∥EF.
求证: AB∥?. ??例2 如图,两个全等的正方形ABCD和ABEF所在平面交于AB,AM=FN求证:MN//面BCEABCDEFMN∵MN // GH∴ MN //面BCE线线平行线面平行方法一:平移法例2 如图,两个全等的正方形ABCD和ABEF所在平面交于AB,AM=FN求证:MN//面BCEABCDEFMN∵△AFN∽ △HNB∴ AN/NH=FN/BN∴ AN/NH=AM/MC∴ MN//CH∴ MN //面BCE方法二:截面法例2 如图,两个全等的正方形ABCD和ABEF所在平面交于AB,AM=FN求证:MN//面BCEABCDEFMN方法三:面面平行G作MG//BC
则AM/MC=AG/GB
又AM/MC=FN/NB
则GN/AF直线与平面平行证明常用方法: 主要用在 ____________情况下 平行、垂直较多 方法好想,书写较繁,一般不能给第二小问提示,最好用截面法.
②截面法:③面面平行:①平移法 :两条相交直线___________确定,线面平行转化为线线平行。截面由常用辅助线:见中点,想中位线
例3 在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1EE∵DB1 // EF∴ DB1 //面A1C1E线线平行线面平行方法一:截面法12例3 在正方体AC1中,E为DD1的中点,求证:DB1//面A1C1EE方法二:面面平行F练习1.如图,在四棱锥P-ABCD中,M,N分别是AB,PC的中点,若ABCD是平行四边形,求证:MN∥平面PAD.PABCDMNQQ练习2.在正方体AC1中,O为平面ADD1A1的中心, 求证:CO // 面A1C1BB1O方法一:截面法练习2.在正方体AC1中,O为平面ADD1A1的中心, 求证:CO // 面A1C1BB1O方法二:面面平行练习3、在直三棱柱ABC—A1B1C1,D是AB中点,求证:AC1∥面B1CDBAA1CADB1C1O方法一:截面法练习3、在直三棱柱ABC—A1B1C1,D是AB中点,求证:AC1∥面B1CDBAA1CADB1C1O方法二:面面平行E六、小结1,直线与平面平行判定定理与性质定理
(1)判定定理:
(2)性质定理
2、直线与平面平行证明常用方法:
①平移法 :
②截面法:
③面面平行:
3,常用辅助线:见中点,想中位线
作业作业:用三种方法证明。如图,M,N分别是正方体ABCD—A1B1C1D1的棱、AA1 , CD1 中点
求证:MN∥面ABCD。MNE方法一:平移法 练习4、如图,M,N分别是正方体ABCD—A1B1C1D1的棱、AA1 , CD1 中点
求证:MN∥面ABCD。MNE方法二:截面法P练习4、如图,M,N分别是正方体ABCD—A1B1C1D1的棱、AA1 , CD1 中点
求证:MN∥面ABCD。MNE方法三:面面平行
