2.1.2 直线的方程 课件 19张PPT
文档属性
| 名称 | 2.1.2 直线的方程 课件 19张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览





文档简介
课件19张PPT。对
自 数
然 学
界 发
的 现
深 最
入 丰 ︱
研 富 ︱
究 的 傅
是 源 里
泉 叶2.直线的倾斜角α 与斜率k的关系是 __________1.过点A(x1,y1)、B (x2,y2) 的直线的斜率k=_______3. 思考:确定一条直线需要几个独立条件?能举例说明吗?温故知新(1)直线上的两点
(2)直线上的一点和直线的倾斜角(斜率)第二章 平面解析几何初步2.1.2 直线的方程
-----点斜式
1.了解由斜率公式推导直线方程的点斜式的过程.
2.学会直线方程的点斜式、斜截式的形式特点及知道其适用范围
3.能够正确利用直线的点斜式、斜截式公式求直线的方程
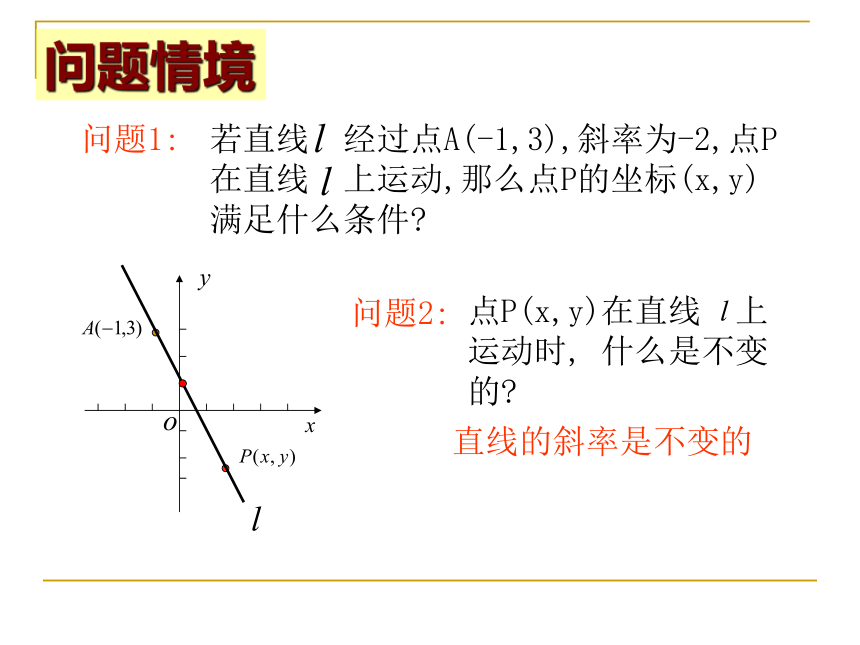
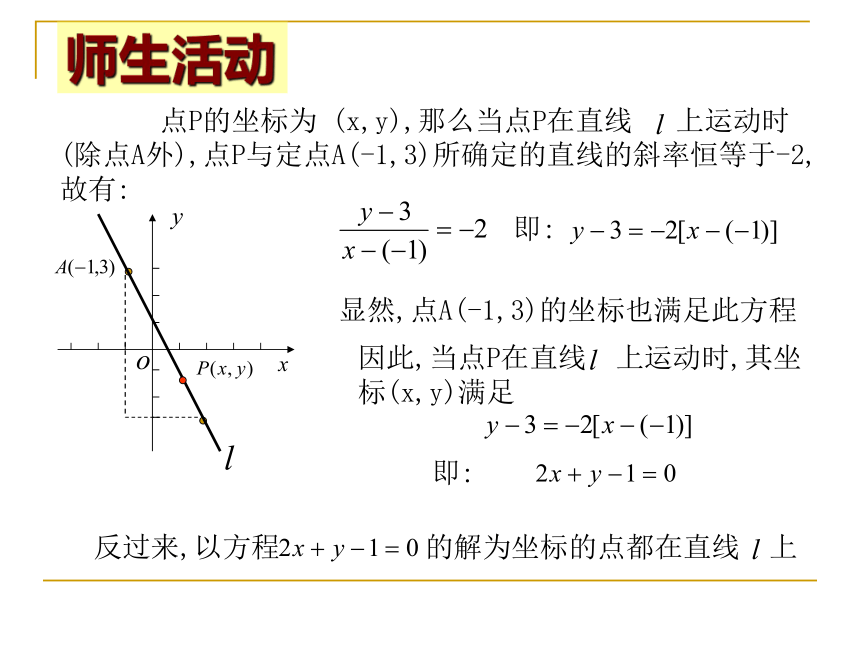
学习目标问题1:问题2:直线的斜率是不变的问题情境 点P的坐标为 (x,y),那么当点P在直线 上运动时(除点A外),点P与定点A(-1,3)所确定的直线的斜率恒等于-2,故有:即:显然,点A(-1,3)的坐标也满足此方程因此,当点P在直线 上运动时,其坐标(x,y)满足即:反过来,以方程的解为坐标的点都在直线 上师生活动问题情境 一般地,设直线 经过点 ,斜率为k,直线 上任意一点P的坐标是(x,y).当点P(x,y)(不同于P1)直线 上运动时,
PP1的斜率恒等于k,即:故: 直线 上的每个点(包括点P1)的坐标都是这个方程的解;反过来,以这个方程的解为坐标的点都在直线 上。⑴⑵问题4:方程⑴和⑵表示同一条直线吗?问题3:满足方程 吗?学生活动经过点 斜率为k的直线 的方程为: 这个方程是由一个点和直线的斜率决定的,所以我们把它叫做直线的点斜式方程1、直线的点斜式方程建构数学问题5:(1)利用点斜式方程求直线方程,需要知道哪些要素?
(2)直角坐标系上任意直线都可以用直线的点斜式方程表示吗?数学运用一、点斜式直线方程
1、只适用于斜率存在的直线
2、已知直线上一点以及直线的斜率
二、特例反思感悟1、经过点 ,且斜率为0的直线的方程是_____________ y=y02、经过点 ,且斜率不存在的直线的方程是_____________ x=x0例2、已知直线 的斜率为k,与y轴的交点是点P(0,b),求直线 的方程.解:由直线的点斜式方程,得:即:所以这个方程也叫做直线的斜截式方程.数学运用 解:例3、直线l的倾斜角?=60o,且l 在 y 轴上的截距为3,求直线l的斜截式方程。而l的斜截式方程为:问题6:斜截式方程的适用范围?
问题7:截距是距离吗?问题8:直线的斜截式方程与一次函数的表达式有什么区别和联系?
斜率存在截距是一个点的横(纵)坐标,是一个实数,可以是正数,也可以是负数和零,而距离是一个非负数.截距不是距离只有当k≠0时,斜截式方程才是一次函数的表达式问题9:斜截式与点斜式存在什么关系?斜截式是点斜式的特殊情况,有时比点斜式更方便口答:说出下列直线的斜率和在y轴上的截距:数学运用1.点斜式方程当斜率不存在时不适用2.斜截式方程当斜率不存在时不适用3.特殊情况:当斜率不存在时
课堂小结一、知识点二、思想方法代数方法解决几何问题,由特殊到一般2、y=kx+2和y=x+b表示的直线有什么特征?.(0,2)直线系数学之美1、已知直线上两点 ,根据本节课所学内容你能用这两点表示出直线的方程吗?课本p82页练习1、3、4、5课堂练习数学使人聪明
自 数
然 学
界 发
的 现
深 最
入 丰 ︱
研 富 ︱
究 的 傅
是 源 里
泉 叶2.直线的倾斜角α 与斜率k的关系是 __________1.过点A(x1,y1)、B (x2,y2) 的直线的斜率k=_______3. 思考:确定一条直线需要几个独立条件?能举例说明吗?温故知新(1)直线上的两点
(2)直线上的一点和直线的倾斜角(斜率)第二章 平面解析几何初步2.1.2 直线的方程
-----点斜式
1.了解由斜率公式推导直线方程的点斜式的过程.
2.学会直线方程的点斜式、斜截式的形式特点及知道其适用范围
3.能够正确利用直线的点斜式、斜截式公式求直线的方程
学习目标问题1:问题2:直线的斜率是不变的问题情境 点P的坐标为 (x,y),那么当点P在直线 上运动时(除点A外),点P与定点A(-1,3)所确定的直线的斜率恒等于-2,故有:即:显然,点A(-1,3)的坐标也满足此方程因此,当点P在直线 上运动时,其坐标(x,y)满足即:反过来,以方程的解为坐标的点都在直线 上师生活动问题情境 一般地,设直线 经过点 ,斜率为k,直线 上任意一点P的坐标是(x,y).当点P(x,y)(不同于P1)直线 上运动时,
PP1的斜率恒等于k,即:故: 直线 上的每个点(包括点P1)的坐标都是这个方程的解;反过来,以这个方程的解为坐标的点都在直线 上。⑴⑵问题4:方程⑴和⑵表示同一条直线吗?问题3:满足方程 吗?学生活动经过点 斜率为k的直线 的方程为: 这个方程是由一个点和直线的斜率决定的,所以我们把它叫做直线的点斜式方程1、直线的点斜式方程建构数学问题5:(1)利用点斜式方程求直线方程,需要知道哪些要素?
(2)直角坐标系上任意直线都可以用直线的点斜式方程表示吗?数学运用一、点斜式直线方程
1、只适用于斜率存在的直线
2、已知直线上一点以及直线的斜率
二、特例反思感悟1、经过点 ,且斜率为0的直线的方程是_____________ y=y02、经过点 ,且斜率不存在的直线的方程是_____________ x=x0例2、已知直线 的斜率为k,与y轴的交点是点P(0,b),求直线 的方程.解:由直线的点斜式方程,得:即:所以这个方程也叫做直线的斜截式方程.数学运用 解:例3、直线l的倾斜角?=60o,且l 在 y 轴上的截距为3,求直线l的斜截式方程。而l的斜截式方程为:问题6:斜截式方程的适用范围?
问题7:截距是距离吗?问题8:直线的斜截式方程与一次函数的表达式有什么区别和联系?
斜率存在截距是一个点的横(纵)坐标,是一个实数,可以是正数,也可以是负数和零,而距离是一个非负数.截距不是距离只有当k≠0时,斜截式方程才是一次函数的表达式问题9:斜截式与点斜式存在什么关系?斜截式是点斜式的特殊情况,有时比点斜式更方便口答:说出下列直线的斜率和在y轴上的截距:数学运用1.点斜式方程当斜率不存在时不适用2.斜截式方程当斜率不存在时不适用3.特殊情况:当斜率不存在时
课堂小结一、知识点二、思想方法代数方法解决几何问题,由特殊到一般2、y=kx+2和y=x+b表示的直线有什么特征?.(0,2)直线系数学之美1、已知直线上两点 ,根据本节课所学内容你能用这两点表示出直线的方程吗?课本p82页练习1、3、4、5课堂练习数学使人聪明
