2.2.2 直线与圆的位置关系复习课件19张PPT
文档属性
| 名称 | 2.2.2 直线与圆的位置关系复习课件19张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 729.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 21:34:33 | ||
图片预览





文档简介
课件19张PPT。直线与圆的位置关系复习(1)学习目标:
1、熟练掌握判断直线与圆位置关系的方 法—代数法、几何法.
2、熟练掌握直线与圆相切的处理方法,会求圆的切线方程.
3、会解决直线与圆相交的问题及简单的弦长问题.
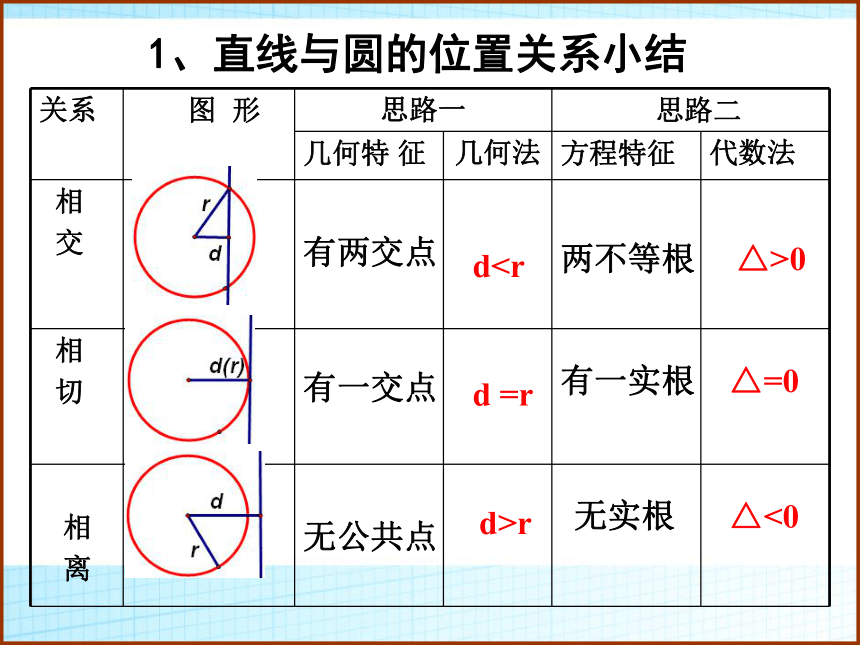
4、会解决简单的有关直线与圆的综合性问题. 1、直线与圆的位置关系小结注意:
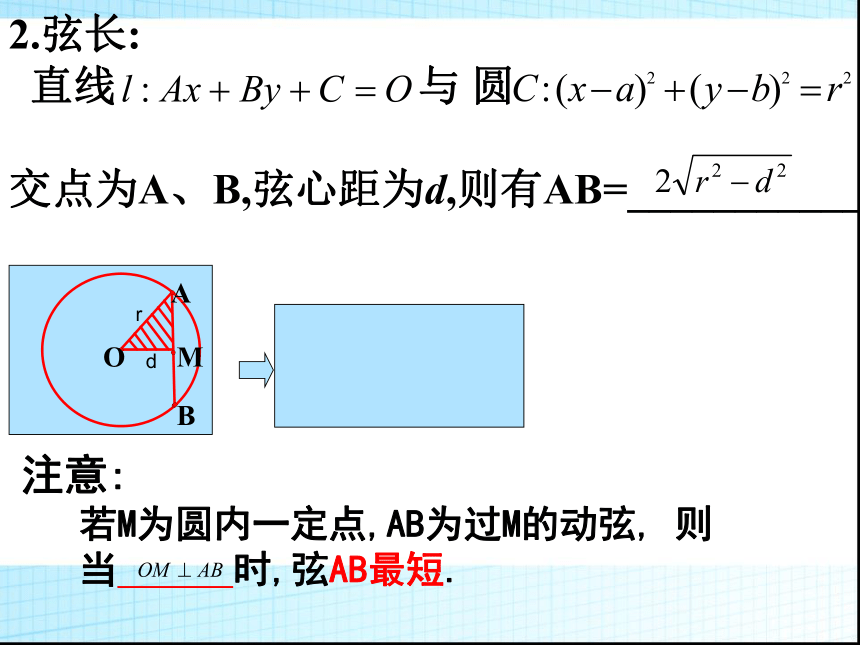
若M为圆内一定点,AB为过M的动弦, 则
当 时,弦AB最短.注意:
在研究与切线有关的问题时要
优先考虑点与圆的位置关系
3.切线1.求法: 2.过一点作圆的切线条数:
利用d=r 若点在圆上则只有一条切线
若点在圆内则没切线
若点在圆外则有两条切线课前练习:2、直线 被圆
截得的弦长为____________1、若直线 与圆
没有公共点,求 的取值范围______________x+2y-5=04a<-5或a>53、若点 在以坐标原点为圆心的圆上,则该圆在
点 处的切线方程为___________例题分析: 例1:(1)求切线方程.解 (1)当斜率不存在时,x=2符合题意,当斜率存在时,设直线的方程为y=k(x-2)即kx-y-2k=0又由圆的方程知圆心为C(1,-3),r=1由点到直线的距离公式得由 d=r得:所以所求切线方程为 4x-3y-8=0或x=2解得?CAB(2,0)?CAB(2,0)解法1:由(1)知,两切点坐标A ,B ,C(1,-3)
设所求圆的方程为
因为A,B,C三点在圆上,故有
C(1,-3)解法2:由题意得,所求圆为以PC为直径的圆,由P(2,0),C(1,-3)
得圆心为 ,?CAB(2,0)C(1,-3)例2.已知点P(0,5)及圆C:
(1)若直线 l 过点P且被圆截得的弦长为 ,求 直线 l 的方程。
(2)求过点P且被圆C截得的弦长最短时的直线的方程。
解(1)由已知得圆心C(-2,6),半径r=4,因为弦长为所以圆心到l的距离为2,当直线的斜率不存在时,直线的方程为x=0,符合题意。
当直线的斜率存在时,设斜率为k,即直线方程可设为y-5=kx,即kx-y+5=0,由公式所以直线方程为3x-4y+20=0故所求的直线方程为3x-4y+20=0或x=0。(2)圆的一般方程可化为(x+2)2+(y-6)2=16,
则圆心为(-2,6) 当CP与弦所在直线垂直时,弦长最短。又所以所求直线斜率为2,所以直线方程为即思考:过点M 的直线 与圆O:
求直线 的方程。解法(1):设圆心到直线的距离为d,则解法(2):巩固练习:1.直线(3k+2)x-ky-2=0(k∈R)与圆x2+y2-2x
-2y-3=0的位置关系是 :_________. 相交3、在平面直角坐标系中,以点(1,0)为圆心且与直线mx-y-2m-1=0(m∈R)相切的所有圆中,半径最大的圆的标准方程为___________________.x+y-2=0或7x+17y+26=0(x-1)2+y2=2小结 本节课我们主要复习了直线与圆的位置关系中切线和弦长的相关问题,以及在处理这些问题的过程中需要注意的地方和所涉及的知识点。
2.求圆心在直线y=-2x上,且与直线y=1-x
相切于点(2,-1)的圆的方程同学们再见!
1、熟练掌握判断直线与圆位置关系的方 法—代数法、几何法.
2、熟练掌握直线与圆相切的处理方法,会求圆的切线方程.
3、会解决直线与圆相交的问题及简单的弦长问题.
4、会解决简单的有关直线与圆的综合性问题. 1、直线与圆的位置关系小结注意:
若M为圆内一定点,AB为过M的动弦, 则
当 时,弦AB最短.注意:
在研究与切线有关的问题时要
优先考虑点与圆的位置关系
3.切线1.求法: 2.过一点作圆的切线条数:
利用d=r 若点在圆上则只有一条切线
若点在圆内则没切线
若点在圆外则有两条切线课前练习:2、直线 被圆
截得的弦长为____________1、若直线 与圆
没有公共点,求 的取值范围______________x+2y-5=04a<-5或a>53、若点 在以坐标原点为圆心的圆上,则该圆在
点 处的切线方程为___________例题分析: 例1:(1)求切线方程.解 (1)当斜率不存在时,x=2符合题意,当斜率存在时,设直线的方程为y=k(x-2)即kx-y-2k=0又由圆的方程知圆心为C(1,-3),r=1由点到直线的距离公式得由 d=r得:所以所求切线方程为 4x-3y-8=0或x=2解得?CAB(2,0)?CAB(2,0)解法1:由(1)知,两切点坐标A ,B ,C(1,-3)
设所求圆的方程为
因为A,B,C三点在圆上,故有
C(1,-3)解法2:由题意得,所求圆为以PC为直径的圆,由P(2,0),C(1,-3)
得圆心为 ,?CAB(2,0)C(1,-3)例2.已知点P(0,5)及圆C:
(1)若直线 l 过点P且被圆截得的弦长为 ,求 直线 l 的方程。
(2)求过点P且被圆C截得的弦长最短时的直线的方程。
解(1)由已知得圆心C(-2,6),半径r=4,因为弦长为所以圆心到l的距离为2,当直线的斜率不存在时,直线的方程为x=0,符合题意。
当直线的斜率存在时,设斜率为k,即直线方程可设为y-5=kx,即kx-y+5=0,由公式所以直线方程为3x-4y+20=0故所求的直线方程为3x-4y+20=0或x=0。(2)圆的一般方程可化为(x+2)2+(y-6)2=16,
则圆心为(-2,6) 当CP与弦所在直线垂直时,弦长最短。又所以所求直线斜率为2,所以直线方程为即思考:过点M 的直线 与圆O:
求直线 的方程。解法(1):设圆心到直线的距离为d,则解法(2):巩固练习:1.直线(3k+2)x-ky-2=0(k∈R)与圆x2+y2-2x
-2y-3=0的位置关系是 :_________. 相交3、在平面直角坐标系中,以点(1,0)为圆心且与直线mx-y-2m-1=0(m∈R)相切的所有圆中,半径最大的圆的标准方程为___________________.x+y-2=0或7x+17y+26=0(x-1)2+y2=2小结 本节课我们主要复习了直线与圆的位置关系中切线和弦长的相关问题,以及在处理这些问题的过程中需要注意的地方和所涉及的知识点。
2.求圆心在直线y=-2x上,且与直线y=1-x
相切于点(2,-1)的圆的方程同学们再见!
