3.1.2用二分法求方程的近似解 (共29张PPT)
文档属性
| 名称 | 3.1.2用二分法求方程的近似解 (共29张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 686.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 21:13:26 | ||
图片预览








文档简介
(共29张PPT)
3.1.2 用二分法求方程
的近似解
ax2+bx+c=0
x2+x-6=0
新课导入
回想一下上一节课所学的内容.
(1)函数的零点及其等价关系?
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
(2)如何求零点个数及所在区间?
解一:利用计算器或计算机作
的对应
那么函数
在区间
内至少有一个实数
有且只有一个零点、再在其它区间内去寻找.
上连续,并且有
值表,若在区间
在
上的单调性,则在
根、若能证明
解二:试探着找到两个x对应的函数值为一正一负(至少有一个);再证单调增函数即可得有且只有一个.
解三:构造两个易画函数,画图,看图象与x轴交点个数,很实用.
(3)连续函数在某个区间上存在零点的判别方法:
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点.
即存在c∈(a,b),使得f(c )=0,这个c也就是方程f(x)=0的根.
从学校教学楼到学校食堂的电缆有5个接点.现在某处发生故障,需及时修理.为了尽快把故障缩小在两个接点之间,一般至少需要检查多少___次.
2
1 2 3 4 5
猜数字游戏,看谁先猜中
10次以内猜出,你们能做到吗 ?
从1~1000这1000个自然数随机抽出1个数,谁能根据提示“大了”“小了”“对了”先猜出这个数?
想一想
思考
一元二次方程可以用公式求根,但没有公式可用来求lnx+2x-6=0的根,能否利用函数的有关知识来求它根的近似值呢?
探究1
2.你能继续缩小零点所在的区间吗?
1.你能找出零点落在下列哪个区间吗?
√
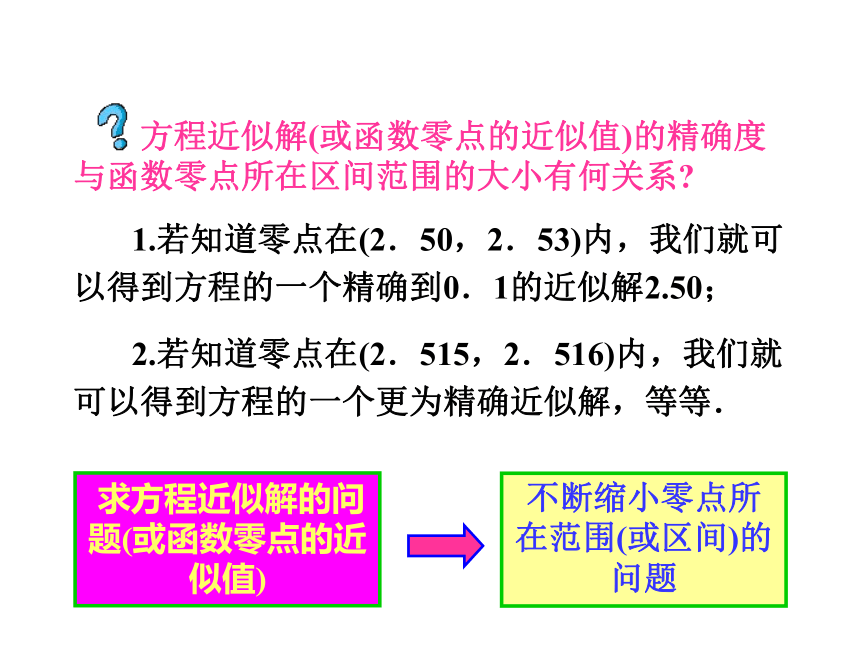
方程近似解(或函数零点的近似值)的精确度与函数零点所在区间范围的大小有何关系?
1.若知道零点在(2.50,2.53)内,我们就可以得到方程的一个精确到0.1的近似解2.50;
2.若知道零点在(2.515,2.516)内,我们就可以得到方程的一个更为精确近似解,等等.
求方程近似解的问题(或函数零点的近似值)
不断缩小零点所在范围(或区间)的问题
如何缩小零点所在的范围,得到一个越来越小的区间,以使零点仍在此区间内?
将一个区间分为两个区间.
取中点
该找怎样的分点?
如果不为0,通过比较中点与两个端点函数值的正负,即可判知零点是在 内,还是在 内,从而将零点所在范围缩小了一半.
对于一个已知的零点所在区间(a,b),取中点 ,计算 ,根据零点所在范围的判断方法,如果这个函数值为0,那么中点就是函数的零点;
(a,b) 中点x1 f(a) f(x1)
(2 , 3) 2.5 负 -0.084
(2.5,3) 2.75 负 0.512
(2.5,2.75) 2.625 负 0.215
(2.5,2.625) 2.5625 负 0.066
(2.5,2.5625) 2.53125 负 -0.009
(2.53125,2.5625) 2.546875 负 0.029
(2.53125,2.546875) 2.5390625 负 0.010
(2.53125,2.5390625) 2.53515625 负 0.001
f(b)
正
正
正
正
正
正
正
正
| 2.5390625 -2.53125|=0.0078125<0.01
精确度已达到0.01
这种运用缩小零点所在范围的方法在数学和计算机科学上被称为二分法.
对于区间[a,b]上连续不断且f(a) ·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).
二分法的实质就是将函数零点所在的区间不断地一分为二,使新得到的区间不断变小,两个端点逐步逼近零点.
思考:下列函数中哪个能用二分法求零点?
√
二分法求方程近似解的一般步骤:
1、确定区间[a,b],验证f(a)f(b)<0,给定精确度ε.
2、求区间(a,b)的中点c.
3、计算f(c);
(1) 若f(c)=0,则c就是函数的零点
(2) 若f(a)f(c)<0,则令b= c(此时零点x0∈(a,c))
(3) 若f(a)f(c)>0,则令a= c(此时零点x0∈(c,b))
4、判断是否达到精确度ε,即若|a-b|< ε,则得到零点的近似值a(或b);否则重复2~4.
由|a-b|<ε可知,区间[a,b]中任意一个值都是零点x0 的满足精确度ε的近似值,这是为什么呢?(当然为了方便,这里统一取区间端点a(或b)作为零点的近似值)
思考
例: 求出方程x2-2x-1=0的一个近似解(精确度0.1)
解:做出函数f(x)=x2-2x-1的对应值表与图像.
x -1 0 1 2 3
f(x) 2 -1 -2 -1 2
由图可知道此函数在区间(-1,0)与(2,3)内有零点.
-1
-2
-2
-1
1
1
2
3
2
o
x
y
在区间(2,3)中
由于
所以方程的一个近似解可取为2.4375.
在区间(-1,0)中同理可得到方程的另外一个近似解为0.375.
综上所述方程的近似解分别是0.375,2.4375.
用二分法求函数的零点近似值的方法仅对函数的变号零点适合,对函数的不变号零点不适用.
注意
例:用二分法求方程
在区间(-1,0)内的近似解(精确度0.1)
易知:f(-1)<0,f(0)>0
取x=-0.5,计算f(-0.5)≈3.375>0
取x=-0.75,计算f(-0.75)≈1.58>0
解:
取x=-0.875,计算f(-0.875)≈0.39>0
取x=-0.9375,计算f(-0.9375)≈-0.28<0
∴ 原方程的近似解取为-0.9375
对于在区间[a,b]上连续不断、且f(a)f(b)<0的函数y=f(x),通过不断把函数f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法.
课堂小结
1.二分法
2.概括利用二分法求函数f(x)零点的近似值的步骤
1.确定区间[a,b],验证 ,给定精确度
2.求区间(a,b)的中点c.
3.计算f(c)
(1)若f(c)=0,则c 就是函数的零点;
(2)若 ,则令b=0(此零点 );
4.判断是否达到精确度 :即若 ,则得到零点 近似值a(或b);否则重复步骤2-4.
(3)若 ,则令a=0(此时零点 ).
课堂练习
1.下列函数中能用二分法求零点的是( )
x
y
0
x
y
0
x
y
0
x
y
0
A
B
C
D
B
2.用二分法求函数y=f(x)在 内零点近似值的过程中得到f(1)<0,f(1.5)>0,f(1.25)<0,则函数的零点落在区间( )
A.(1,1.25) B.(1.25,1.5)
C. (1.5,2) D.不能确定
A
3.已知函数
的图象与x轴的交点至少有一个在原点右侧,则
实数m的取值范围是( )
B.
D.
A.
C.
D
4.已知函数
的图象如图所示,则
1
2
B.
C.
D.
A.
3.1.2 用二分法求方程
的近似解
ax2+bx+c=0
x2+x-6=0
新课导入
回想一下上一节课所学的内容.
(1)函数的零点及其等价关系?
对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.
方程f(x)=0有实数根
函数y=f(x)的图象与x轴有交点
函数y=f(x)有零点
(2)如何求零点个数及所在区间?
解一:利用计算器或计算机作
的对应
那么函数
在区间
内至少有一个实数
有且只有一个零点、再在其它区间内去寻找.
上连续,并且有
值表,若在区间
在
上的单调性,则在
根、若能证明
解二:试探着找到两个x对应的函数值为一正一负(至少有一个);再证单调增函数即可得有且只有一个.
解三:构造两个易画函数,画图,看图象与x轴交点个数,很实用.
(3)连续函数在某个区间上存在零点的判别方法:
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点.
即存在c∈(a,b),使得f(c )=0,这个c也就是方程f(x)=0的根.
从学校教学楼到学校食堂的电缆有5个接点.现在某处发生故障,需及时修理.为了尽快把故障缩小在两个接点之间,一般至少需要检查多少___次.
2
1 2 3 4 5
猜数字游戏,看谁先猜中
10次以内猜出,你们能做到吗 ?
从1~1000这1000个自然数随机抽出1个数,谁能根据提示“大了”“小了”“对了”先猜出这个数?
想一想
思考
一元二次方程可以用公式求根,但没有公式可用来求lnx+2x-6=0的根,能否利用函数的有关知识来求它根的近似值呢?
探究1
2.你能继续缩小零点所在的区间吗?
1.你能找出零点落在下列哪个区间吗?
√
方程近似解(或函数零点的近似值)的精确度与函数零点所在区间范围的大小有何关系?
1.若知道零点在(2.50,2.53)内,我们就可以得到方程的一个精确到0.1的近似解2.50;
2.若知道零点在(2.515,2.516)内,我们就可以得到方程的一个更为精确近似解,等等.
求方程近似解的问题(或函数零点的近似值)
不断缩小零点所在范围(或区间)的问题
如何缩小零点所在的范围,得到一个越来越小的区间,以使零点仍在此区间内?
将一个区间分为两个区间.
取中点
该找怎样的分点?
如果不为0,通过比较中点与两个端点函数值的正负,即可判知零点是在 内,还是在 内,从而将零点所在范围缩小了一半.
对于一个已知的零点所在区间(a,b),取中点 ,计算 ,根据零点所在范围的判断方法,如果这个函数值为0,那么中点就是函数的零点;
(a,b) 中点x1 f(a) f(x1)
(2 , 3) 2.5 负 -0.084
(2.5,3) 2.75 负 0.512
(2.5,2.75) 2.625 负 0.215
(2.5,2.625) 2.5625 负 0.066
(2.5,2.5625) 2.53125 负 -0.009
(2.53125,2.5625) 2.546875 负 0.029
(2.53125,2.546875) 2.5390625 负 0.010
(2.53125,2.5390625) 2.53515625 负 0.001
f(b)
正
正
正
正
正
正
正
正
| 2.5390625 -2.53125|=0.0078125<0.01
精确度已达到0.01
这种运用缩小零点所在范围的方法在数学和计算机科学上被称为二分法.
对于区间[a,b]上连续不断且f(a) ·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法(bisection).
二分法的实质就是将函数零点所在的区间不断地一分为二,使新得到的区间不断变小,两个端点逐步逼近零点.
思考:下列函数中哪个能用二分法求零点?
√
二分法求方程近似解的一般步骤:
1、确定区间[a,b],验证f(a)f(b)<0,给定精确度ε.
2、求区间(a,b)的中点c.
3、计算f(c);
(1) 若f(c)=0,则c就是函数的零点
(2) 若f(a)f(c)<0,则令b= c(此时零点x0∈(a,c))
(3) 若f(a)f(c)>0,则令a= c(此时零点x0∈(c,b))
4、判断是否达到精确度ε,即若|a-b|< ε,则得到零点的近似值a(或b);否则重复2~4.
由|a-b|<ε可知,区间[a,b]中任意一个值都是零点x0 的满足精确度ε的近似值,这是为什么呢?(当然为了方便,这里统一取区间端点a(或b)作为零点的近似值)
思考
例: 求出方程x2-2x-1=0的一个近似解(精确度0.1)
解:做出函数f(x)=x2-2x-1的对应值表与图像.
x -1 0 1 2 3
f(x) 2 -1 -2 -1 2
由图可知道此函数在区间(-1,0)与(2,3)内有零点.
-1
-2
-2
-1
1
1
2
3
2
o
x
y
在区间(2,3)中
由于
所以方程的一个近似解可取为2.4375.
在区间(-1,0)中同理可得到方程的另外一个近似解为0.375.
综上所述方程的近似解分别是0.375,2.4375.
用二分法求函数的零点近似值的方法仅对函数的变号零点适合,对函数的不变号零点不适用.
注意
例:用二分法求方程
在区间(-1,0)内的近似解(精确度0.1)
易知:f(-1)<0,f(0)>0
取x=-0.5,计算f(-0.5)≈3.375>0
取x=-0.75,计算f(-0.75)≈1.58>0
解:
取x=-0.875,计算f(-0.875)≈0.39>0
取x=-0.9375,计算f(-0.9375)≈-0.28<0
∴ 原方程的近似解取为-0.9375
对于在区间[a,b]上连续不断、且f(a)f(b)<0的函数y=f(x),通过不断把函数f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法.
课堂小结
1.二分法
2.概括利用二分法求函数f(x)零点的近似值的步骤
1.确定区间[a,b],验证 ,给定精确度
2.求区间(a,b)的中点c.
3.计算f(c)
(1)若f(c)=0,则c 就是函数的零点;
(2)若 ,则令b=0(此零点 );
4.判断是否达到精确度 :即若 ,则得到零点 近似值a(或b);否则重复步骤2-4.
(3)若 ,则令a=0(此时零点 ).
课堂练习
1.下列函数中能用二分法求零点的是( )
x
y
0
x
y
0
x
y
0
x
y
0
A
B
C
D
B
2.用二分法求函数y=f(x)在 内零点近似值的过程中得到f(1)<0,f(1.5)>0,f(1.25)<0,则函数的零点落在区间( )
A.(1,1.25) B.(1.25,1.5)
C. (1.5,2) D.不能确定
A
3.已知函数
的图象与x轴的交点至少有一个在原点右侧,则
实数m的取值范围是( )
B.
D.
A.
C.
D
4.已知函数
的图象如图所示,则
1
2
B.
C.
D.
A.
