2.1.1 简单随机抽样 课件 28张PPT
文档属性
| 名称 | 2.1.1 简单随机抽样 课件 28张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 421.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 21:44:57 | ||
图片预览







文档简介
课件28张PPT。 2.1 抽样方法复习回顾1、总体:所有考察对象的全体叫做总体。2、个体:构成总体的每一个元素叫做个体。3、样本:从总体中抽取的一部分个体做总体的一个样本。4、样本容量:样本中个体的数目叫做样本容量。5、抽样:从总体中抽取样本的过程叫做抽样。情境2.学校的投影仪灯泡的平均使用寿命是3000小时,“3000小时”这样一个数据是如何得出的呢?1.如何科学、合理地收集数据?
2.怎样分析和研究数据,对一般情况作出估计?问题:问题情境情境1.假设你作为一名食品卫生工作人员,要对某食品店内的一批小包装饼干进行卫生达标检验,你准备怎样做?统 计统计学:统计的基本思想: 用样本估计总体,即通常不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况。 统计学的研究对象是客观事物的数量特征和数量关系,它是关于数据的搜集、整理、归纳和分析方法的科学。当总体容量很大或检测过程具有一定的破坏性时,不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况。那么,如何科学地进行抽样呢? 探究一:如何科学地进行抽样检查? 在1936年美国总统选举前,一份颇有名气的杂志的工作人员做了一次民意调查。调查兰顿(当时任堪萨斯州州长)和罗斯福(当时的总统)中谁将当选下一届总统。为了了解公众意向,调查者通过电话簿和车辆登记簿上的名单给一大批人发了调查表(注意在1936年电话和汽车只有少数富人拥有)。通过分析收回的调查表,显示兰顿非常受欢迎,于是杂志预测兰顿将在选举中获胜。
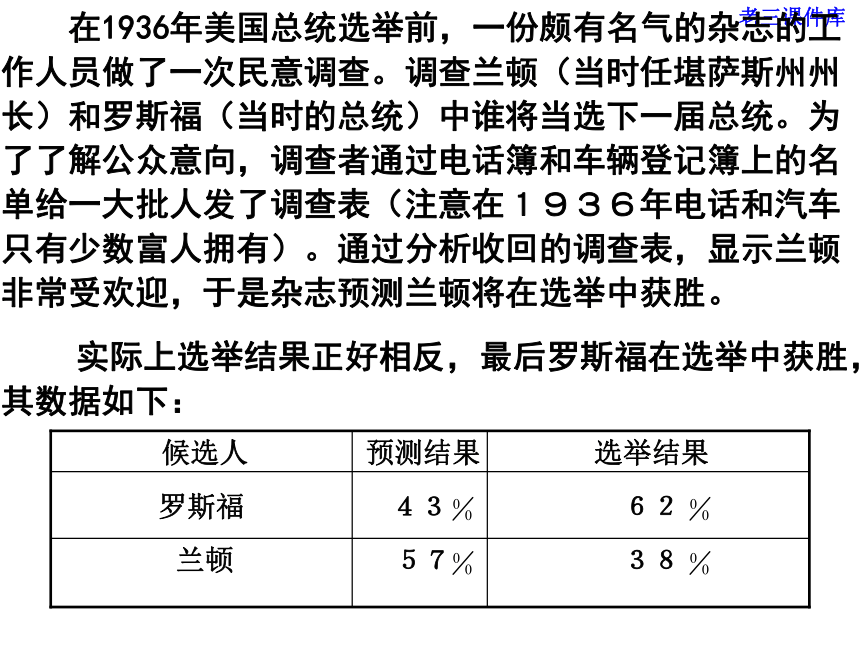
实际上选举结果正好相反,最后罗斯福在选举中获胜,其数据如下:?思考 你认为预期结果出错的原因是什么? 原因是:用于统计推断的样本来自少数富人,只能代表富人的观点,不能代表全体选民的观点(样本不具有代表性)。 像本例中这样容易得到的样本称为方便样本。如果使用“方便样本”,由于“方便样本”的代表性差,那么得出与事实不符的结论的可能性就会大大增加。 探究二:品尝一勺汤,就可以知道一锅汤的味道,你知道其中蕴涵的道理吗? 高质量的样本数据来自“搅拌均匀”的总体。如果我们能够设法将总体“搅拌均匀”,那么从中任意抽取一部分个体的样本,它们含有与总体基本相同的信息。“搅拌均匀” 即“使得总体中的每一个个体
都以相同的可能性被选到样本之中”.那么简单随机抽样的含义如何? 简单随机抽样常用的方法:(2)随机数表法.(1)抽签法;2.1.1简单随机抽样 为了了解高一(4)班46名同学的视力情况,从中抽取10名同学进行检查。(2)如何抽取呢?请问: 抽签法实 例 一(1)此例中总体、个体、样本、样本容量 分别是什么? 开始抽签法46名同学从1到46编号制作1到46号签将46个号签搅拌均匀随机从中抽出10个签对号码一致的学生检查结束抽签法的一般步骤:(1)将总体中的N个个体编号;(2)将这N个号码写在形状、大小相同的号签上;(3)将号签放在同一箱中,并搅拌均匀;(4)从箱中每次抽出1个号签,连续抽出k次;(5)将总体中与抽到的号签编号一致的k个个体取出。(总体个数N,样本容量k)开始编号制签搅匀抽签取出个体结束抽签法的一般步骤:(1)将总体中的N个个体编号;(2)将这N个号码写在形状、大小相同的号签上;(3)将号签放在同一箱中,并搅拌均匀;(4)从箱中每次抽出1个号签,连续抽出k次;(5)将总体中与抽到的号签编号一致的k个个体取出。(总体个数N,样本容量k)思考:你认为抽签法有什么优点和缺点?优点:当总体个数较少时,抽签法能够保证每个个体入样的机会相等.
缺点:
(1)当总体中的个数较多时,制作号签的成本将会增加,使得抽签法成本高(费时、费力);
(2)号签很多时,把它们“搅拌均匀”就比样困难,结果很难保证每个个体入样的可能性相等,从而使产生坏样本(即代表性差的样本)的可能性增加.随机数表法随机数表 下面通过例子来说明,假设我们要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,可以按照下面的步骤进行.第一步,先将800袋牛奶编号,可以编为000,001,…,
799 .第二步,在随机数表中任选一个数,例如选出第8行
第7列的数7.随机数表法(为了便于说明,下面摘取了表的第6行至第10行).第三步,从选定的数7开始向右读(读数的方向也可以是向左、向上、向下等),得到一个三位数785,由于785<799,说明号码785在总体内,将它取出;继续向右读,得到916,由于916>799,将它去掉,按照这种方法继续向右读,又取出567,199,507,…,依次下去,直到样本的60个号码全部取出,这样我们就得到一个容量为60的样本. ①对总体中的个体进行编号(每个号码位数一致);
②在随机数表中任选一个数作为开始;
③从选定的数开始按一定方向读下去,若得到的号码在编号中,则取出;若在不编号中或前面已经取出,则跳过;如此进行下去,直到取满为止;
④根据选定的号码抽取样本。随机数表法抽取样本的步骤:简单随机抽样 一般地,从个体数为N的总体中逐个不放回地取n个个体作为样本(n(1)简单随机抽样要求被抽取的样本的总体个数
N是有限的。
(2)样本数n小于样本总体的个数N.
(3)样本是从总体中逐个抽取的。
(4)简单随机抽样是一种不放回的抽样。
(5)简单随机抽样的每个个体入样的可能性均为n/N.例题1: 中央电视台要从春节联欢晚会的60名热心观众中随机抽出4名幸运观众,试用抽签法为其设计产生这4名幸运观众的过程.数学运用 评点:抽签法—编号、制签、搅拌、抽取,关键是“搅拌”后的随机性.
随机数表法—编号、选数、取号、抽取,其中取号的方向具有任意性. 某车间工人加工一种轴100件,为了了解这种轴的直径,要从中抽取10件轴在同一条件下测量,如何采用简单随机抽样的方法抽取样本?例题2:数学运用解法1:(抽签法)将100件轴编号为1,2,…,100,并做好大小、形状相同的号签,分别写上这100个数,将这些号签放在一起,进行均匀搅拌,接着连续抽取10个号签,然后测量这个10个号签对应的轴的直径。
解法2:(随机数表法)将100件轴编号为00,01,…99,在随机数表中选定一个起始位置,如取第21行第1个数开始,选取10个为68,34,30,13,70,55,74,77,40,44,这10件即为所要抽取的样本。1.下列抽取样本的方式是属于简单随机抽样的是( )
①从无限多个个体中抽取100个个体作样本;
②盒子里有80个零件,从中选出5个零件进行质量检验,在抽样操作时,从中任意拿出一个零件进行质量检验后,再把它放回盒子里;
③从8台电脑中不放回的随机抽取2台进行质量检验(假设8台电脑已编好号,对编号随机抽取)
A.① B.② C.③ D.以上都不对C想一想:什么样的总体适宜简单随机抽样?适用范围:总体的个体数不多时。课堂练习2.今年某市有6万名学生参加升学考试,为了了解6万名考生的数学成绩, 从中抽取1500名考生的数学成绩进行统计分析,以下正确的说法是 ( )
A.6万名考生是总体
B.每名考生的数学成绩是个体
C.1500名考生是总体的一个样本
D.1500名是样本容量B课堂练习(3)练习:p46 1、2、3、4思考: 人们打掼蛋牌时,将洗好的扑克牌随机确定一张为起始牌,这时按次序抓牌时,对任何一家来说,都是从108张牌中抽取27张牌,问这种抽样方法是否是简单随机抽样?[分析] 简单随机抽样的实质是逐个地从总体中随机抽取样本,而这里只是随机确定了起始张,其它各张牌虽然是逐张抓牌,但是各张在谁手里已被确定,所以不是简单随机抽样.注:随机抽样并不是随意或随便抽取,因为随意或随便抽取都会带有主观或客观的影响因素. 1、简单随机抽样的定义;
2、抽签法(抓阄法)的一般步骤;
3、随机数表法的一般步骤;
4、抽签法与随机数表法的比较。【课堂小结】
2.怎样分析和研究数据,对一般情况作出估计?问题:问题情境情境1.假设你作为一名食品卫生工作人员,要对某食品店内的一批小包装饼干进行卫生达标检验,你准备怎样做?统 计统计学:统计的基本思想: 用样本估计总体,即通常不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况。 统计学的研究对象是客观事物的数量特征和数量关系,它是关于数据的搜集、整理、归纳和分析方法的科学。当总体容量很大或检测过程具有一定的破坏性时,不直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况。那么,如何科学地进行抽样呢? 探究一:如何科学地进行抽样检查? 在1936年美国总统选举前,一份颇有名气的杂志的工作人员做了一次民意调查。调查兰顿(当时任堪萨斯州州长)和罗斯福(当时的总统)中谁将当选下一届总统。为了了解公众意向,调查者通过电话簿和车辆登记簿上的名单给一大批人发了调查表(注意在1936年电话和汽车只有少数富人拥有)。通过分析收回的调查表,显示兰顿非常受欢迎,于是杂志预测兰顿将在选举中获胜。
实际上选举结果正好相反,最后罗斯福在选举中获胜,其数据如下:?思考 你认为预期结果出错的原因是什么? 原因是:用于统计推断的样本来自少数富人,只能代表富人的观点,不能代表全体选民的观点(样本不具有代表性)。 像本例中这样容易得到的样本称为方便样本。如果使用“方便样本”,由于“方便样本”的代表性差,那么得出与事实不符的结论的可能性就会大大增加。 探究二:品尝一勺汤,就可以知道一锅汤的味道,你知道其中蕴涵的道理吗? 高质量的样本数据来自“搅拌均匀”的总体。如果我们能够设法将总体“搅拌均匀”,那么从中任意抽取一部分个体的样本,它们含有与总体基本相同的信息。“搅拌均匀” 即“使得总体中的每一个个体
都以相同的可能性被选到样本之中”.那么简单随机抽样的含义如何? 简单随机抽样常用的方法:(2)随机数表法.(1)抽签法;2.1.1简单随机抽样 为了了解高一(4)班46名同学的视力情况,从中抽取10名同学进行检查。(2)如何抽取呢?请问: 抽签法实 例 一(1)此例中总体、个体、样本、样本容量 分别是什么? 开始抽签法46名同学从1到46编号制作1到46号签将46个号签搅拌均匀随机从中抽出10个签对号码一致的学生检查结束抽签法的一般步骤:(1)将总体中的N个个体编号;(2)将这N个号码写在形状、大小相同的号签上;(3)将号签放在同一箱中,并搅拌均匀;(4)从箱中每次抽出1个号签,连续抽出k次;(5)将总体中与抽到的号签编号一致的k个个体取出。(总体个数N,样本容量k)开始编号制签搅匀抽签取出个体结束抽签法的一般步骤:(1)将总体中的N个个体编号;(2)将这N个号码写在形状、大小相同的号签上;(3)将号签放在同一箱中,并搅拌均匀;(4)从箱中每次抽出1个号签,连续抽出k次;(5)将总体中与抽到的号签编号一致的k个个体取出。(总体个数N,样本容量k)思考:你认为抽签法有什么优点和缺点?优点:当总体个数较少时,抽签法能够保证每个个体入样的机会相等.
缺点:
(1)当总体中的个数较多时,制作号签的成本将会增加,使得抽签法成本高(费时、费力);
(2)号签很多时,把它们“搅拌均匀”就比样困难,结果很难保证每个个体入样的可能性相等,从而使产生坏样本(即代表性差的样本)的可能性增加.随机数表法随机数表 下面通过例子来说明,假设我们要考察某公司生产的500克袋装牛奶的质量是否达标,现从800袋牛奶中抽取60袋进行检验,利用随机数表抽取样本时,可以按照下面的步骤进行.第一步,先将800袋牛奶编号,可以编为000,001,…,
799 .第二步,在随机数表中任选一个数,例如选出第8行
第7列的数7.随机数表法(为了便于说明,下面摘取了表的第6行至第10行).第三步,从选定的数7开始向右读(读数的方向也可以是向左、向上、向下等),得到一个三位数785,由于785<799,说明号码785在总体内,将它取出;继续向右读,得到916,由于916>799,将它去掉,按照这种方法继续向右读,又取出567,199,507,…,依次下去,直到样本的60个号码全部取出,这样我们就得到一个容量为60的样本. ①对总体中的个体进行编号(每个号码位数一致);
②在随机数表中任选一个数作为开始;
③从选定的数开始按一定方向读下去,若得到的号码在编号中,则取出;若在不编号中或前面已经取出,则跳过;如此进行下去,直到取满为止;
④根据选定的号码抽取样本。随机数表法抽取样本的步骤:简单随机抽样 一般地,从个体数为N的总体中逐个不放回地取n个个体作为样本(n
N是有限的。
(2)样本数n小于样本总体的个数N.
(3)样本是从总体中逐个抽取的。
(4)简单随机抽样是一种不放回的抽样。
(5)简单随机抽样的每个个体入样的可能性均为n/N.例题1: 中央电视台要从春节联欢晚会的60名热心观众中随机抽出4名幸运观众,试用抽签法为其设计产生这4名幸运观众的过程.数学运用 评点:抽签法—编号、制签、搅拌、抽取,关键是“搅拌”后的随机性.
随机数表法—编号、选数、取号、抽取,其中取号的方向具有任意性. 某车间工人加工一种轴100件,为了了解这种轴的直径,要从中抽取10件轴在同一条件下测量,如何采用简单随机抽样的方法抽取样本?例题2:数学运用解法1:(抽签法)将100件轴编号为1,2,…,100,并做好大小、形状相同的号签,分别写上这100个数,将这些号签放在一起,进行均匀搅拌,接着连续抽取10个号签,然后测量这个10个号签对应的轴的直径。
解法2:(随机数表法)将100件轴编号为00,01,…99,在随机数表中选定一个起始位置,如取第21行第1个数开始,选取10个为68,34,30,13,70,55,74,77,40,44,这10件即为所要抽取的样本。1.下列抽取样本的方式是属于简单随机抽样的是( )
①从无限多个个体中抽取100个个体作样本;
②盒子里有80个零件,从中选出5个零件进行质量检验,在抽样操作时,从中任意拿出一个零件进行质量检验后,再把它放回盒子里;
③从8台电脑中不放回的随机抽取2台进行质量检验(假设8台电脑已编好号,对编号随机抽取)
A.① B.② C.③ D.以上都不对C想一想:什么样的总体适宜简单随机抽样?适用范围:总体的个体数不多时。课堂练习2.今年某市有6万名学生参加升学考试,为了了解6万名考生的数学成绩, 从中抽取1500名考生的数学成绩进行统计分析,以下正确的说法是 ( )
A.6万名考生是总体
B.每名考生的数学成绩是个体
C.1500名考生是总体的一个样本
D.1500名是样本容量B课堂练习(3)练习:p46 1、2、3、4思考: 人们打掼蛋牌时,将洗好的扑克牌随机确定一张为起始牌,这时按次序抓牌时,对任何一家来说,都是从108张牌中抽取27张牌,问这种抽样方法是否是简单随机抽样?[分析] 简单随机抽样的实质是逐个地从总体中随机抽取样本,而这里只是随机确定了起始张,其它各张牌虽然是逐张抓牌,但是各张在谁手里已被确定,所以不是简单随机抽样.注:随机抽样并不是随意或随便抽取,因为随意或随便抽取都会带有主观或客观的影响因素. 1、简单随机抽样的定义;
2、抽签法(抓阄法)的一般步骤;
3、随机数表法的一般步骤;
4、抽签法与随机数表法的比较。【课堂小结】
