2.4.1 线性回归方程(1)课件 18张PPT
文档属性
| 名称 | 2.4.1 线性回归方程(1)课件 18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览






文档简介
课件18张PPT。高中数学苏教版 必修32.4 线性回归方程(1) 某小卖部为了了解热茶销售量与气温之间的关系,随机统计并制作了某6天卖出热茶的杯数与当天气温的对照表:问题探究
气温和热茶卖出去的杯数有什么样的关系? 如果某天的气温是-50C,你能根据这些数据预测这天小卖部卖处热茶的杯数吗?思考 数学成绩y与学习数学所用时间t之间的关系,能否用函数关系刻画?一般来说,学数学的时间越长,成绩越好.但用时10小时,数学成绩却不是一个确定的数字.故不能用函数关系刻画.答案思考:两个变量之间的常见关系有几种?(1)确定性的函数关系,变量之间的关系可以用函数表示.
(2)相关关系,变量之间有一定的联系,但不能完全用函数来表示.1.球的体积和球的半径具有( )
A.函数关系 B.相关关系
C.不确定关系 D.无任何关系2.下列两个变量之间的关系不是函数关系的是( )
A.角的度数和正弦值
B.速度一定时,距离和时间的关系
C.正方体的棱长和体积
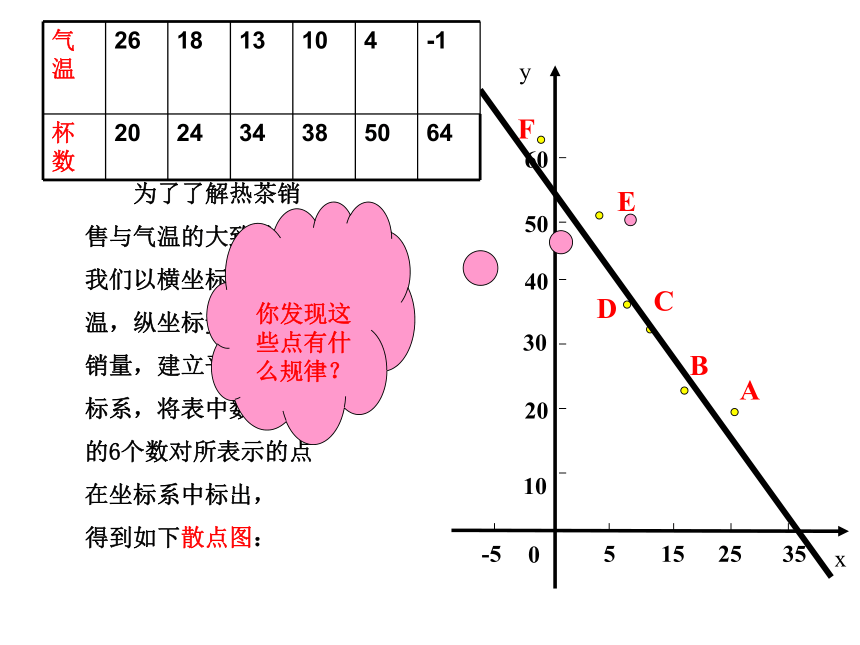
D.日照时间和水稻的亩产量AD 概念辨析 为了了解热茶销
售与气温的大致关系,
我们以横坐标x表示气
温,纵坐标y表示热茶
销量,建立平面直角坐
标系,将表中数据构成
的6个数对所表示的点
在坐标系中标出,
得到如下散点图:
你发现这些点有什么规律?答:都分布在同一条直线的附近.象这样能用直线方程 来表示两个变量之间的相关关系我们把它称为线性相关关系.思考 怎样衡量直线 与图中6个点地接近程度呢?类比估计总体平均数地思想,考虑离差的平方和
探究 Q(a,b)=它们与表中相应的实际值应该越接近越好. 以上公式的推导较复杂,故不作推导,但它的原理较为简单:即各点到该直线的距离的平方和最小,这一方法叫最小二乘法. 若上面数据满足线性相关关系,那么
则称为这n个数据的线性回归方程.
其中 如果某天的气温是-50C,你能根据这些数据预测这天小卖部卖处热茶的杯数吗? 某小卖部为了了解热茶销售量与气温之间的系,随机统计并制作了某6天卖出热茶的杯数与当天气温的对照表: 线性回归方程的求法及应用例1 下表为某地近几年机动车辆数与交通事故数的统计资料,请判断机动车辆数与交通事故数之间是否具有线性相关关系.如果具有线性相关关系,求出线性回归方程;如果不具有线性相关关系,说明理由.在直角坐标系中画出数据的散点图如图:
直观判断散点在一条直线附近,故具有线性相关关系.从而计算相应的数据之和:
课堂练习:
1. 求三点(3,10),(7,20),(11,24)的线性回归方程.解(1)作出散点图:2.如图所示的五组数据(x,y)中,去掉________后,剩下的4组数据相关性增强.2341去除(4,10)后,其余四点大致分布在一条直线附近,相关性增强.(4,10)答案解析3.设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小平方法建立的线性回归方程为 =0.85x-85.71,则下列结论中不正确的是_____.
①体重y与身高x具有函数间的关系;
②回归直线过 点;
③若该大学某女生身高增加1 cm,则其体重约增加0.85 kg;
④若该大学某女生身高为170 cm,则可判定其体重必为58.79 kg.2341体重与身高的关系不确定,不是函数关系.当x=170时, =0.85×170
-85.71=58.79,体重的估计值为58.79 kg.①④答案解析求解线性回归问题的步骤:
1.列表( ),画散点图.
2.计算:
3.代入公式求a,b
4.列出直线方程
气温和热茶卖出去的杯数有什么样的关系? 如果某天的气温是-50C,你能根据这些数据预测这天小卖部卖处热茶的杯数吗?思考 数学成绩y与学习数学所用时间t之间的关系,能否用函数关系刻画?一般来说,学数学的时间越长,成绩越好.但用时10小时,数学成绩却不是一个确定的数字.故不能用函数关系刻画.答案思考:两个变量之间的常见关系有几种?(1)确定性的函数关系,变量之间的关系可以用函数表示.
(2)相关关系,变量之间有一定的联系,但不能完全用函数来表示.1.球的体积和球的半径具有( )
A.函数关系 B.相关关系
C.不确定关系 D.无任何关系2.下列两个变量之间的关系不是函数关系的是( )
A.角的度数和正弦值
B.速度一定时,距离和时间的关系
C.正方体的棱长和体积
D.日照时间和水稻的亩产量AD 概念辨析 为了了解热茶销
售与气温的大致关系,
我们以横坐标x表示气
温,纵坐标y表示热茶
销量,建立平面直角坐
标系,将表中数据构成
的6个数对所表示的点
在坐标系中标出,
得到如下散点图:
你发现这些点有什么规律?答:都分布在同一条直线的附近.象这样能用直线方程 来表示两个变量之间的相关关系我们把它称为线性相关关系.思考 怎样衡量直线 与图中6个点地接近程度呢?类比估计总体平均数地思想,考虑离差的平方和
探究 Q(a,b)=它们与表中相应的实际值应该越接近越好. 以上公式的推导较复杂,故不作推导,但它的原理较为简单:即各点到该直线的距离的平方和最小,这一方法叫最小二乘法. 若上面数据满足线性相关关系,那么
则称为这n个数据的线性回归方程.
其中 如果某天的气温是-50C,你能根据这些数据预测这天小卖部卖处热茶的杯数吗? 某小卖部为了了解热茶销售量与气温之间的系,随机统计并制作了某6天卖出热茶的杯数与当天气温的对照表: 线性回归方程的求法及应用例1 下表为某地近几年机动车辆数与交通事故数的统计资料,请判断机动车辆数与交通事故数之间是否具有线性相关关系.如果具有线性相关关系,求出线性回归方程;如果不具有线性相关关系,说明理由.在直角坐标系中画出数据的散点图如图:
直观判断散点在一条直线附近,故具有线性相关关系.从而计算相应的数据之和:
课堂练习:
1. 求三点(3,10),(7,20),(11,24)的线性回归方程.解(1)作出散点图:2.如图所示的五组数据(x,y)中,去掉________后,剩下的4组数据相关性增强.2341去除(4,10)后,其余四点大致分布在一条直线附近,相关性增强.(4,10)答案解析3.设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小平方法建立的线性回归方程为 =0.85x-85.71,则下列结论中不正确的是_____.
①体重y与身高x具有函数间的关系;
②回归直线过 点;
③若该大学某女生身高增加1 cm,则其体重约增加0.85 kg;
④若该大学某女生身高为170 cm,则可判定其体重必为58.79 kg.2341体重与身高的关系不确定,不是函数关系.当x=170时, =0.85×170
-85.71=58.79,体重的估计值为58.79 kg.①④答案解析求解线性回归问题的步骤:
1.列表( ),画散点图.
2.计算:
3.代入公式求a,b
4.列出直线方程
