3.1.2 随机事件的概率 课件 18张PPT
文档属性
| 名称 | 3.1.2 随机事件的概率 课件 18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览




文档简介
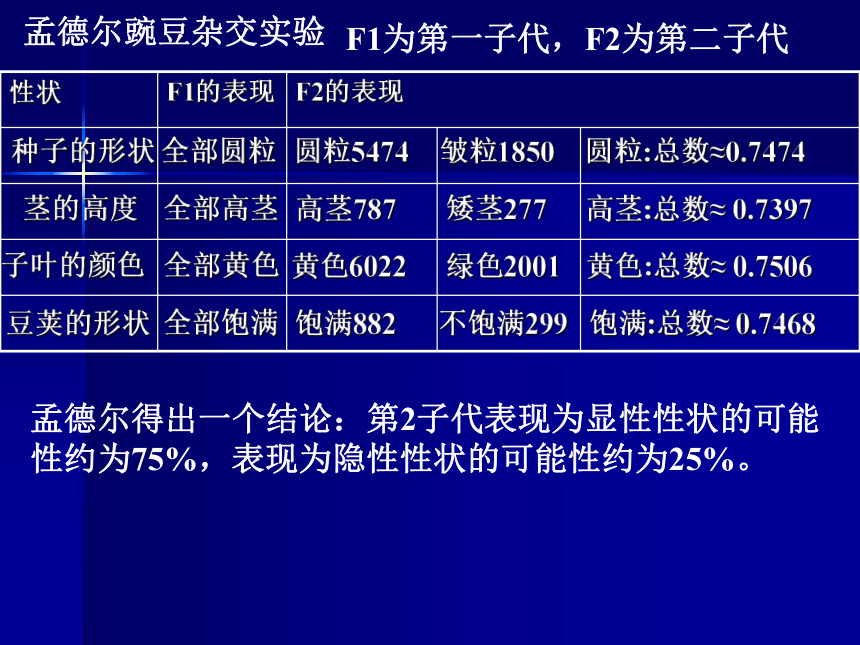
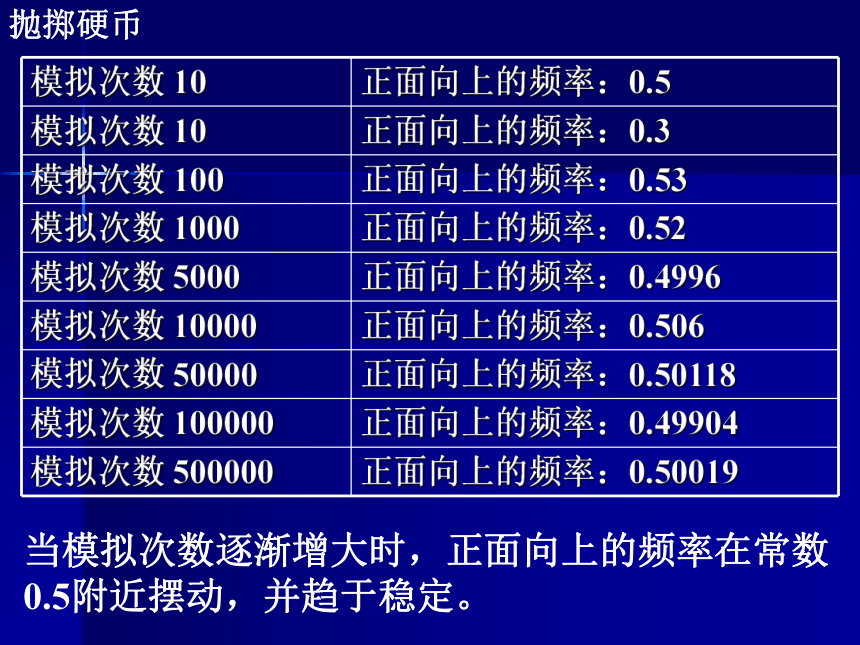
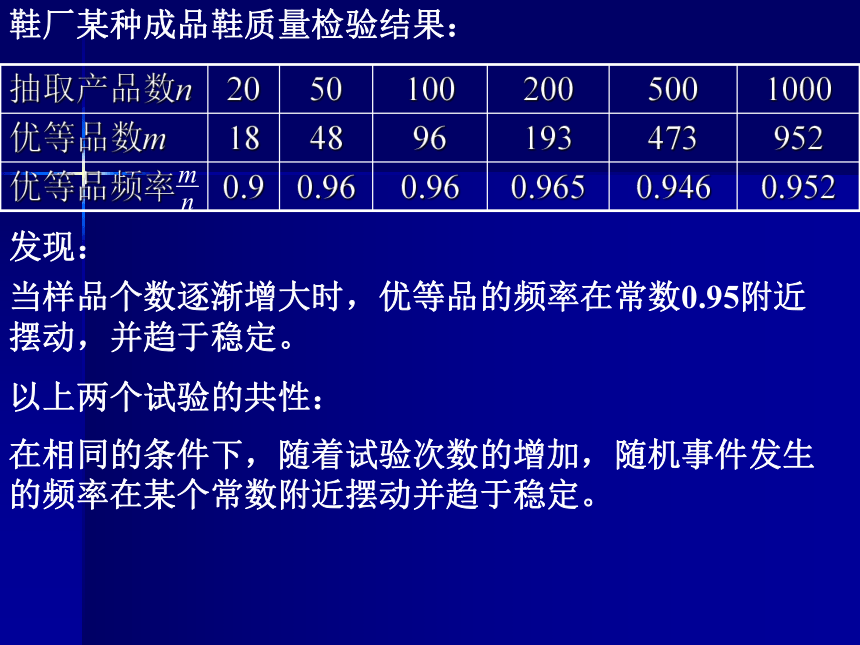
课件18张PPT。随机事件的概率我们已经学习过用概率表示一个事件再一次试验或观测中发生的可能性的大小,它是在0~1之间的一个数,将这个事件记为A,用P(A)表示事件A发生的概率,对于任意一个随机事件A,P(A)必须满足如下基本关系:问:怎样确定一个事件发生的概率?孟德尔豌豆杂交实验F1为第一子代,F2为第二子代孟德尔得出一个结论:第2子代表现为显性性状的可能性约为75%,表现为隐性性状的可能性约为25%。抛掷硬币当模拟次数逐渐增大时,正面向上的频率在常数0.5附近摆动,并趋于稳定。历史上有很多人做过相关试验鞋厂某种成品鞋质量检验结果:发现:当样品个数逐渐增大时,优等品的频率在常数0.95附近摆动,并趋于稳定。以上两个试验的共性:在相同的条件下,随着试验次数的增加,随机事件发生的频率在某个常数附近摆动并趋于稳定。一般地,对于给定的随机事件A,在相同条件下,随着试验次数的增加,事件A发生的频率会在某个常数附近摆动,并趋于稳定,我们可以用这个常数来刻画随机事件A发生的可能性的大小,并把这个常数称为随机事件A的概率(probability),记作P(A).以上两个试验的共性:在相同的条件下,随着试验次数的增加,随机事件发生的频率在某个常数附近摆动并趋于稳定。概率的统计定义:说明:1、求概率的一个基本方法:通过大量重复试验2、概率与频率的关系:3、必然事件Ω,P(Ω)=1;不可能事件Φ,P(Φ)=0概率另一种近似求法: 概率是频率的的稳定值,而频率是概率的近似值。概念辨析DD甲说:“如果他前9个问题都回答正确,则第10个问题,一定回答错误.”这句话对吗?乙说:“如果他第一个问题回答错误,则后一个问题回答正确的概率大于90%.”这句话对吗?偶然性与必然性---------对立与统一不对不对例1、某油菜籽在相同条件下的发芽率试验结果如下表:(1)将油菜籽发芽的频率填入表中(2)这种油菜籽发芽的概率约为多少?10.80.90.860.890.920.910.890.900.91例2、某市1999-2002年新生儿出生数及其中男婴数(单位:人)如下(1)试计算男婴各年出生的频率(精确到0.001)(2)该市男婴出生的概率约为多少?练习:2、某次数学考试有12个选择题,每题都是四选一,某人说:“每个选择支正确的概率是1/4,我每题都选第一个选择支,则一定有3道题的选择结果正确,这句话对吗?1、掷一枚硬币,连续出现5次正面向上,甲认为下次出现反面向上的概率大于1/2,你同意吗?为什么?练习:3、下表是π前n位小数中,数字6出现的次数,0.090.080.0960.0940.10.1020.10040.9955(1)计算6出现的频率(2)6出现的概率约为多少?猜一猜:掷两枚均匀的硬币,正面都向上的概率约是多少呢?小结:1、概率的统计定义3、概率与频率之间的关系2、概率的求法课后作业:1、课本P97 1,2,3,4,52、思考题:请你设计一个方案,来计算“守株待兔”成功的概率。再见
