3.2.1 古典概型 课件 21张PPT
文档属性
| 名称 | 3.2.1 古典概型 课件 21张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 580.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览





文档简介
课件21张PPT。情境引入:意大利数学家卡当(1501-1576)提出这样一个问题: 甲、乙两个人掷两颗骰子,以两颗骰子的点数和打赌,甲压4点,乙压11点,请问谁赢的机会比较大?§3.2 古典概型必修三第三章概率 对于某个现象,如果能让其条件实现一次,那么就是进行了一次试验。 在一定条件下,可能发生,也可能不发生的事件叫做随机事件。2.事件:试验中出现的每一种可能的结果,都是一个事件。1.试验:3.随机事件:4.上一节内容我们是如何探究一个随机事件A发生的概率? 问题1:用模拟试验的方法来求某一随机事件
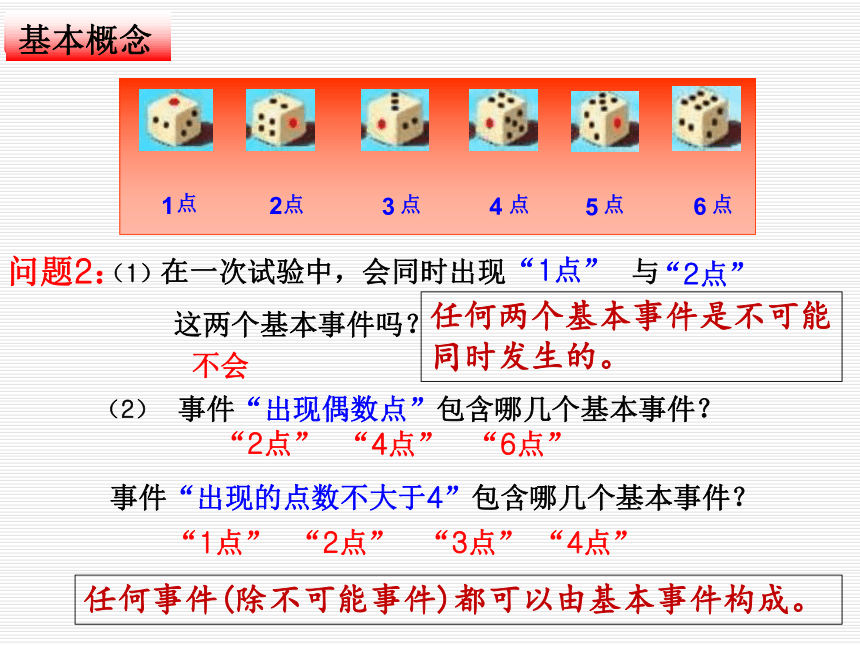
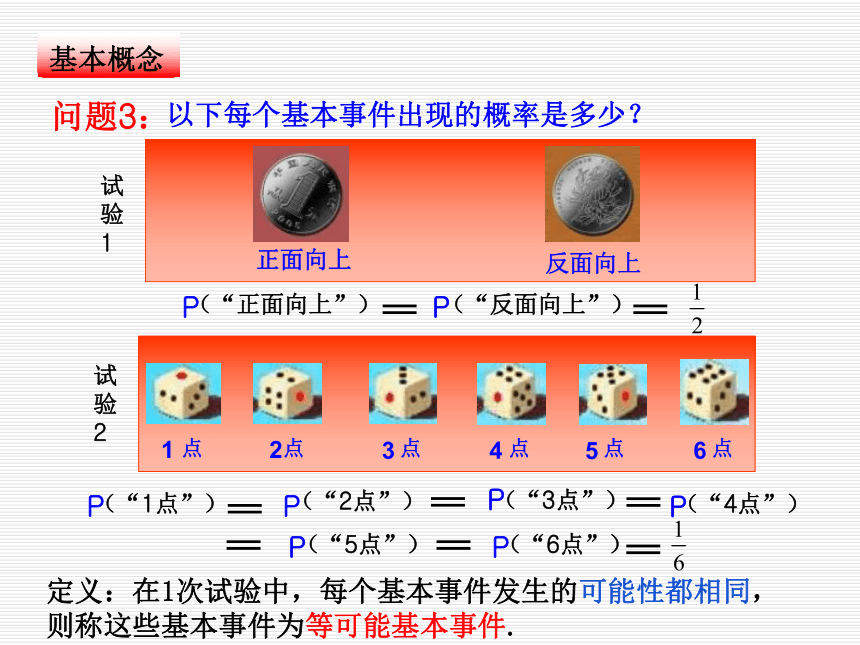
的概率好不好?为什么?试验2:掷一颗均匀的骰子一次,观察出现的点数有哪几种结果?试验1:掷一枚质地均匀的硬币一次,观察朝上的面出现哪几种结果?2 种6 种定义:123456点点点点点点问题2:(1)(2)事件“出现偶数点”包含哪几个基本事件?“2点”“4点”“6点”不会任何两个基本事件是不可能同时发生的。任何事件(除不可能事件)都可以由基本事件构成。事件“出现的点数不大于4”包含哪几个基本事件?“1点”“2点”“3点”“4点”问题3:以下每个基本事件出现的概率是多少?试验 1试验 2定义:在1次试验中,每个基本事件发生的可能性都相同,则称这些基本事件为等可能基本事件.六个基本事件
的概率都是 “1点”、“2点”
“3点”、“4点”
“5点”、“6点” “正面朝上”
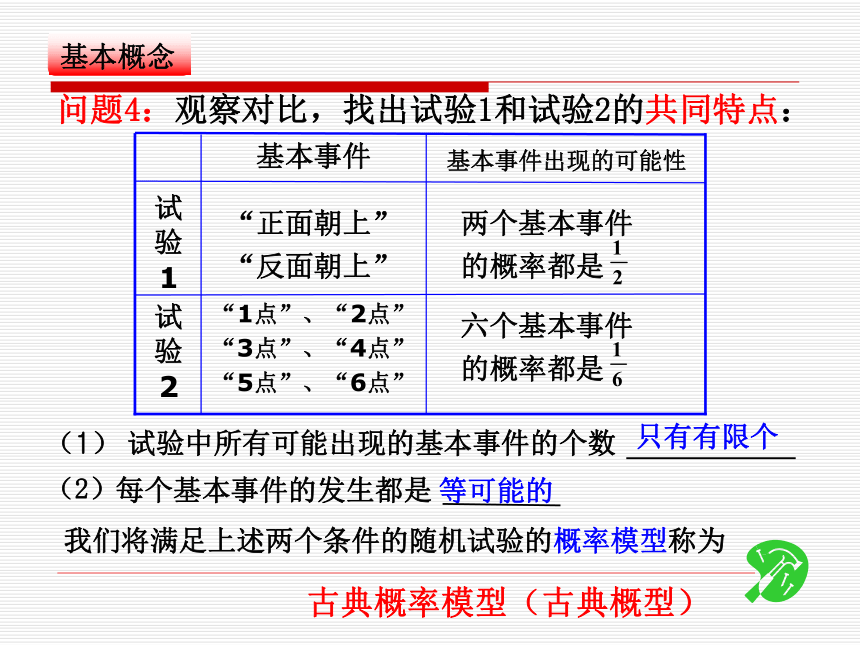
“反面朝上” 基本事件试验2试验1基本事件出现的可能性两个基本事件
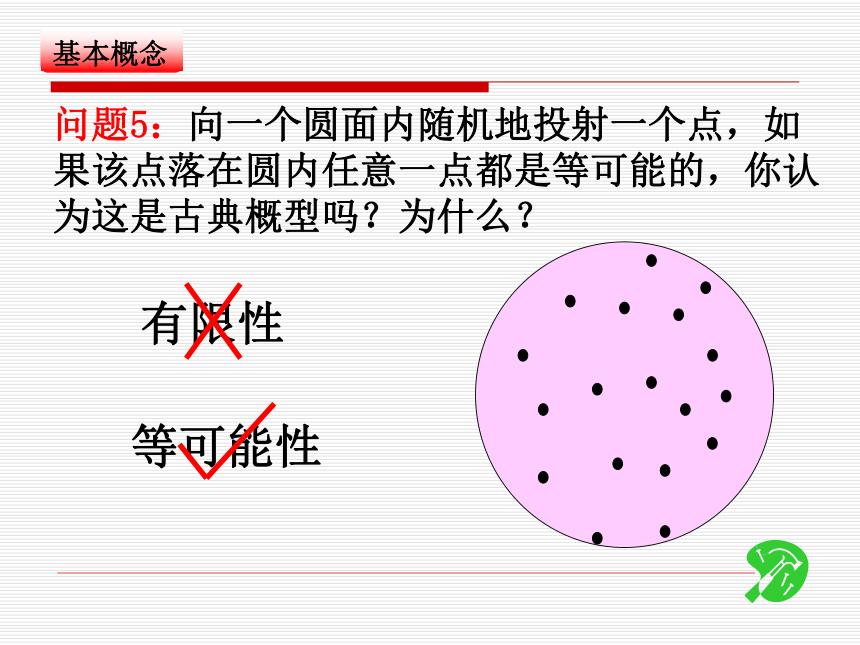
的概率都是 问题4:观察对比,找出试验1和试验2的共同特点:只有有限个等可能的我们将满足上述两个条件的随机试验的概率模型称为古典概率模型(古典概型)问题5:向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么?有限性等可能性问题6:你还能举出生活中的古典概型例子吗?小结:如何判断一个随机试验是否为古典概型? 掷一颗均匀的骰子,试验2:为“出现偶数点”,记事件A请问事件 A发生的概率是多少?探讨:事件A 包含 个基本事件:2点4点6点3基本事件总数为:6?631点,2点,3点,4点,5点,6点问题8:你能总结出古典概型的概率计算公式吗?问题7:在古典概型下,随机事件发生的概率又如何计算呢?(A)P事件A包含的基本事件的个数(m)基本事件的总数(n)古典概型的概率计算公式:要判断所用概率模型是不是古典概型(前提)在使用古典概型的概率公式时,应该注意:例1:盒子中有10个大小相同的球,分别有号码1,2,3,…,10,从中任取一个球,求此球的号码为奇数的概率?分析:这是古典概型吗?满足古典概型两个条件吗?总结:你能说出古典概型解题一般步骤吗?第二步:求出试验所有的基本事件总数n和
随机事件A包含的基本事件个数m;第三步:利用公式求解.第一步:判断是否为古典概型(两个条件);解:(1)掷一个骰子的结果有6种,它总共出现的情况如下所示:从图中可以看出同时掷两个骰子的结果共有36种。
树状图
例2.同时抛两颗骰子,观察向上的点数,问:
(1)共有多少种不同的可能结果?法二:掷一个骰子的结果有6种,我们把两个骰子标上记号1,2以便区分,它总共出现的情况如下表所示:从表中可以看出同时掷两个骰子的结果共有36种。列表法一般适用于分两步完成的结果的列举。解:记“点数之和是3的倍数”为事件A, (2)点数之和是3的倍数的可能结果有多少种?(3)点数之和是3的倍数的概率是多少?则事件A包含12个基本事件; 为什么要把两个骰子标上记号?如果不标记号会出现什么情况?你能解释其中的原因吗? (3,6)(3,3)? 例2.同时抛两颗骰子,观察向上的点数,问:
点数之和是3的倍数的概率是多少?引入问题回答 :
甲乙两个人打赌:
掷两颗骰子,以两颗骰子的点数和打赌,
甲压4点,乙压11点,谁赢的机会比较大?6543216543211号骰子 2号骰子 昨天(11月22日)感恩节,欧尚超市为了回馈顾客,组织了摸奖活动,奖项设置一等奖和二等奖。摸奖箱中有大小、形状均相同,编号为1、2、3的红球和编号为4、5的蓝球。游戏规则:要求一次摸两个球。
你能帮助超市设计一个中奖方案吗?本节课我收获到了什么?一、内容与知识点随机事件的概率还有其他概率模型吗?有限性与等可能性求解步骤(规范)二、思想方法: 探究方法与数学思想:两个条件:公式:基本事件常用表示法:由特殊到一般的思想;数形结合的思想;列举法(树形图、坐标等),不重不漏。问题是数学的心脏.
——哈尔莫斯寄语:
的概率好不好?为什么?试验2:掷一颗均匀的骰子一次,观察出现的点数有哪几种结果?试验1:掷一枚质地均匀的硬币一次,观察朝上的面出现哪几种结果?2 种6 种定义:123456点点点点点点问题2:(1)(2)事件“出现偶数点”包含哪几个基本事件?“2点”“4点”“6点”不会任何两个基本事件是不可能同时发生的。任何事件(除不可能事件)都可以由基本事件构成。事件“出现的点数不大于4”包含哪几个基本事件?“1点”“2点”“3点”“4点”问题3:以下每个基本事件出现的概率是多少?试验 1试验 2定义:在1次试验中,每个基本事件发生的可能性都相同,则称这些基本事件为等可能基本事件.六个基本事件
的概率都是 “1点”、“2点”
“3点”、“4点”
“5点”、“6点” “正面朝上”
“反面朝上” 基本事件试验2试验1基本事件出现的可能性两个基本事件
的概率都是 问题4:观察对比,找出试验1和试验2的共同特点:只有有限个等可能的我们将满足上述两个条件的随机试验的概率模型称为古典概率模型(古典概型)问题5:向一个圆面内随机地投射一个点,如果该点落在圆内任意一点都是等可能的,你认为这是古典概型吗?为什么?有限性等可能性问题6:你还能举出生活中的古典概型例子吗?小结:如何判断一个随机试验是否为古典概型? 掷一颗均匀的骰子,试验2:为“出现偶数点”,记事件A请问事件 A发生的概率是多少?探讨:事件A 包含 个基本事件:2点4点6点3基本事件总数为:6?631点,2点,3点,4点,5点,6点问题8:你能总结出古典概型的概率计算公式吗?问题7:在古典概型下,随机事件发生的概率又如何计算呢?(A)P事件A包含的基本事件的个数(m)基本事件的总数(n)古典概型的概率计算公式:要判断所用概率模型是不是古典概型(前提)在使用古典概型的概率公式时,应该注意:例1:盒子中有10个大小相同的球,分别有号码1,2,3,…,10,从中任取一个球,求此球的号码为奇数的概率?分析:这是古典概型吗?满足古典概型两个条件吗?总结:你能说出古典概型解题一般步骤吗?第二步:求出试验所有的基本事件总数n和
随机事件A包含的基本事件个数m;第三步:利用公式求解.第一步:判断是否为古典概型(两个条件);解:(1)掷一个骰子的结果有6种,它总共出现的情况如下所示:从图中可以看出同时掷两个骰子的结果共有36种。
树状图
例2.同时抛两颗骰子,观察向上的点数,问:
(1)共有多少种不同的可能结果?法二:掷一个骰子的结果有6种,我们把两个骰子标上记号1,2以便区分,它总共出现的情况如下表所示:从表中可以看出同时掷两个骰子的结果共有36种。列表法一般适用于分两步完成的结果的列举。解:记“点数之和是3的倍数”为事件A, (2)点数之和是3的倍数的可能结果有多少种?(3)点数之和是3的倍数的概率是多少?则事件A包含12个基本事件; 为什么要把两个骰子标上记号?如果不标记号会出现什么情况?你能解释其中的原因吗? (3,6)(3,3)? 例2.同时抛两颗骰子,观察向上的点数,问:
点数之和是3的倍数的概率是多少?引入问题回答 :
甲乙两个人打赌:
掷两颗骰子,以两颗骰子的点数和打赌,
甲压4点,乙压11点,谁赢的机会比较大?6543216543211号骰子 2号骰子 昨天(11月22日)感恩节,欧尚超市为了回馈顾客,组织了摸奖活动,奖项设置一等奖和二等奖。摸奖箱中有大小、形状均相同,编号为1、2、3的红球和编号为4、5的蓝球。游戏规则:要求一次摸两个球。
你能帮助超市设计一个中奖方案吗?本节课我收获到了什么?一、内容与知识点随机事件的概率还有其他概率模型吗?有限性与等可能性求解步骤(规范)二、思想方法: 探究方法与数学思想:两个条件:公式:基本事件常用表示法:由特殊到一般的思想;数形结合的思想;列举法(树形图、坐标等),不重不漏。问题是数学的心脏.
——哈尔莫斯寄语:
