1.2基本算法语句的精彩妙用 习题课件 27张PPT
文档属性
| 名称 | 1.2基本算法语句的精彩妙用 习题课件 27张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 23:18:02 | ||
图片预览








文档简介
课件27张PPT。1、课本、练习本、双色笔
2、分析错因,自纠错题
3、标记疑难,以备讨论课前准备判断 满足 赋值输入输出条件循环判断满足不满足结束复习回顾:最近几节课学习过哪些基本算法语句?循环习题1.2 基本算法语句的精彩妙用作业中存在的问题:
1. 不会合理选择算法表示题目中的意图;
2. 条件语句嵌套不熟练,导致算法过程出错;
3.循环语句的结束条件容易出错。失败带给我的经验与收获,在于我已经知道这样做不会成功的证明,下一次
我可以避免同样的错误了。 ——爱迪生 察,然后知不足学习目标:
1. 掌握基本算法语句,能够准确计算出简单的算法程序结果;
2. 结合具体情境,使用算法语句设计出一个算法程序解决问题。 习题3.输入3个数 a,b,c,如果这3个数能作为一个三角形的三边长,那么输出 ,否则提示重新输入.试用算法语句表示上述过程。Read a,b,c
If a+b>c 且b+c>a 且c+a>b Then
P←(a+b+c)/2
Else
Print “请重新输入”
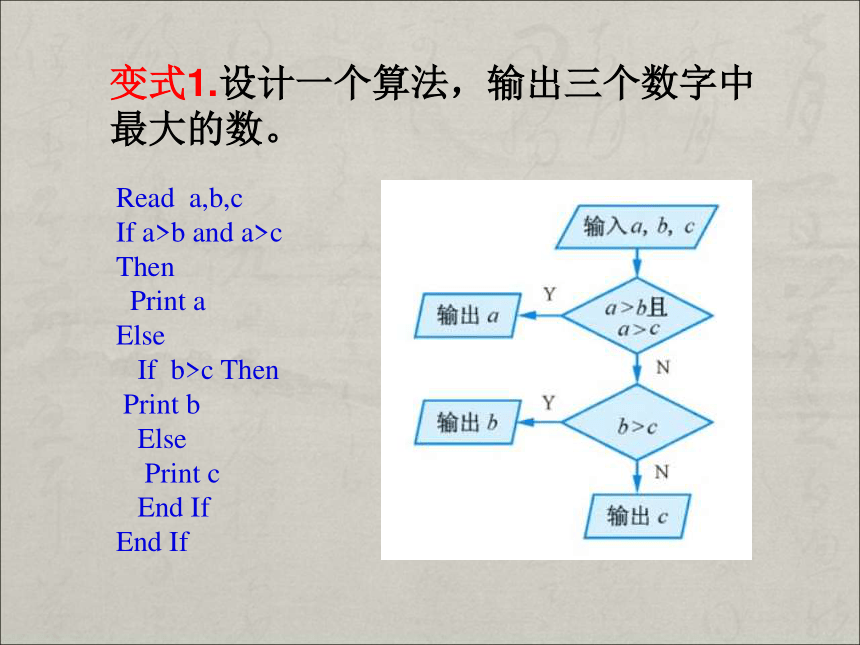
End P变式1.设计一个算法,输出三个数字中最大的数。Read a,b,c
If a>b and a>c Then
Print a
Else
If b>c Then
Print b
Else
Print c
End If
End If 习题5.写出求所有立方小于1000的正整数的一个算法,画出流程图,写出伪代码.习题7.用循环语句描述求式子
一个算法(要求使用三种循环语句表示)。S←0
a←1
For i From 1 To 100
S ←S+a/i
i ←i+1
a ←a*(-1)
End For
print S变式2.设计一个算法描述中国古代数学文化《算法统宗》全称《新编直指算法统宗》,是中国古代数学名著,是明代数学家程大位所著。他搜集了许多古籍,遍访名师,经过数十年的努力,公元1592年六十岁的他终于写成了《直指算法统宗》一书。中国古代数学文化《算法统宗》是一部应用数学书,是以珠算为主要的计算工具,列有595个应用题的数字计算,都不用筹算方法,而是用珠算演算。中国古代数学文化《算法统宗》里很多应用问题都是使用诗歌的表现形式,其中《李白沽酒》就是一篇典型代表。中国古代数学文化诗云:
今携一壶酒,
游春郊外走。
逢朋加一倍,
入店饮斗九。
相逢三处店,
饮尽壶中酒。
试问能算士:
如何知原有?注:古代一斗是10升。大意是:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的19升酒。按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒。想一想:请同学们设计一个算法,计算酒壶里原来有多少升酒?注:古代一斗是升。大意是:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的19升酒。按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒。解法1:解法2:逆向思维
从第三个酒店走回第二个酒店,壶里多少酒呢?
再走回第一个酒店里,壶里多少酒?
最后没进酒店之前有都少酒呢?同学们可以参考情景剧的逆向思维设计一个算法,计算酒壶里原来有多少升酒?a←0
i←0
While i<3
a←
i←i+1
End While
Print a挑战1根据题中的代码,最后输出的a的值为_______a←1
For i From 1 To 100
a←2a+1
End For
Print a挑战2根据题中的代码,最后输出S的值为_______S←0
i←1
While i≤50
S←S+
i←i+1
End While
Print S挑战3根据题中的代码,最后输出S的值为_______S←0
i←1
Do
S←S+i×2i
i←i+1
Until i>10
Print S猜一猜下面的算法描述的是什么问题?a=1
b=1.5
c=0.001
Do
x=(a+b)/2
f(a)= a^3-a-1
f(x)= x^3-x-1
If f (x)=0 Then
Print x
Else
If f(a)*f(x)<0 Then
b=x
Else a=x
End If
End If
Until |a-b| <c
Print x极限挑战猜一猜下面的算法描述的是什么问题?答案是:二分法求方程x^3-x-1=0在区间[1,1.5]上的近似解的一个算法(误差不超过0.001).课堂小结:本节课有哪些收获?1.复习了算法语句,提升对算法语句的理解和应用能力. 2. 培养了数形结合的数学思想. 3.见识了算法和其他章节内容的融合. 4.感受到中国数学文化的源远流长. 思考题:
2、分析错因,自纠错题
3、标记疑难,以备讨论课前准备判断 满足 赋值输入输出条件循环判断满足不满足结束复习回顾:最近几节课学习过哪些基本算法语句?循环习题1.2 基本算法语句的精彩妙用作业中存在的问题:
1. 不会合理选择算法表示题目中的意图;
2. 条件语句嵌套不熟练,导致算法过程出错;
3.循环语句的结束条件容易出错。失败带给我的经验与收获,在于我已经知道这样做不会成功的证明,下一次
我可以避免同样的错误了。 ——爱迪生 察,然后知不足学习目标:
1. 掌握基本算法语句,能够准确计算出简单的算法程序结果;
2. 结合具体情境,使用算法语句设计出一个算法程序解决问题。 习题3.输入3个数 a,b,c,如果这3个数能作为一个三角形的三边长,那么输出 ,否则提示重新输入.试用算法语句表示上述过程。Read a,b,c
If a+b>c 且b+c>a 且c+a>b Then
P←(a+b+c)/2
Else
Print “请重新输入”
End P变式1.设计一个算法,输出三个数字中最大的数。Read a,b,c
If a>b and a>c Then
Print a
Else
If b>c Then
Print b
Else
Print c
End If
End If 习题5.写出求所有立方小于1000的正整数的一个算法,画出流程图,写出伪代码.习题7.用循环语句描述求式子
一个算法(要求使用三种循环语句表示)。S←0
a←1
For i From 1 To 100
S ←S+a/i
i ←i+1
a ←a*(-1)
End For
print S变式2.设计一个算法描述中国古代数学文化《算法统宗》全称《新编直指算法统宗》,是中国古代数学名著,是明代数学家程大位所著。他搜集了许多古籍,遍访名师,经过数十年的努力,公元1592年六十岁的他终于写成了《直指算法统宗》一书。中国古代数学文化《算法统宗》是一部应用数学书,是以珠算为主要的计算工具,列有595个应用题的数字计算,都不用筹算方法,而是用珠算演算。中国古代数学文化《算法统宗》里很多应用问题都是使用诗歌的表现形式,其中《李白沽酒》就是一篇典型代表。中国古代数学文化诗云:
今携一壶酒,
游春郊外走。
逢朋加一倍,
入店饮斗九。
相逢三处店,
饮尽壶中酒。
试问能算士:
如何知原有?注:古代一斗是10升。大意是:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的19升酒。按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒。想一想:请同学们设计一个算法,计算酒壶里原来有多少升酒?注:古代一斗是升。大意是:李白在郊外春游时,做出这样一条约定:遇见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的19升酒。按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒。解法1:解法2:逆向思维
从第三个酒店走回第二个酒店,壶里多少酒呢?
再走回第一个酒店里,壶里多少酒?
最后没进酒店之前有都少酒呢?同学们可以参考情景剧的逆向思维设计一个算法,计算酒壶里原来有多少升酒?a←0
i←0
While i<3
a←
i←i+1
End While
Print a挑战1根据题中的代码,最后输出的a的值为_______a←1
For i From 1 To 100
a←2a+1
End For
Print a挑战2根据题中的代码,最后输出S的值为_______S←0
i←1
While i≤50
S←S+
i←i+1
End While
Print S挑战3根据题中的代码,最后输出S的值为_______S←0
i←1
Do
S←S+i×2i
i←i+1
Until i>10
Print S猜一猜下面的算法描述的是什么问题?a=1
b=1.5
c=0.001
Do
x=(a+b)/2
f(a)= a^3-a-1
f(x)= x^3-x-1
If f (x)=0 Then
Print x
Else
If f(a)*f(x)<0 Then
b=x
Else a=x
End If
End If
Until |a-b| <c
Print x极限挑战猜一猜下面的算法描述的是什么问题?答案是:二分法求方程x^3-x-1=0在区间[1,1.5]上的近似解的一个算法(误差不超过0.001).课堂小结:本节课有哪些收获?1.复习了算法语句,提升对算法语句的理解和应用能力. 2. 培养了数形结合的数学思想. 3.见识了算法和其他章节内容的融合. 4.感受到中国数学文化的源远流长. 思考题:
