2020春人教版数学七年级下册课件:8.3.2用二元一次方程组解决行程、工程等问题(共16张PPT)
文档属性
| 名称 | 2020春人教版数学七年级下册课件:8.3.2用二元一次方程组解决行程、工程等问题(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第八章
8.3 实际问题与二元一次方程组
8.3.2 用二元一次方程组解决行程、工程等问题
教学目标
1.经历和体验用方程组解决实际问题的过程;(重点)
2.在寻求解决问题的过程中建立适当的方程组模型.(难点)
新课导入
路程=______× ;
工作总量= × .
速度
时间
工作效率
工作时间
解:设甲、乙的速度分别为x km/h, y km/h.
根据题意得
例1: 甲、乙两地相距4km, 以各自的速度同时出发. 如果同向而行, 甲2h追上乙; 如果相向而行, 两人0.5h后相遇. 试问两人的速度各是多少?
解方程组, 得
答:甲的速度为5km/h, 乙的速度为3km/h.
新知探究
新知探究
例2: 悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄?
顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
解:设悟空行走速度是每分钟 x里, 风速是每分钟 y里, 则
4(x-y)=600,
x=200,
y=50.
答: 风速是每分钟50里.
4(x+y)=1000,
解得
依题意得
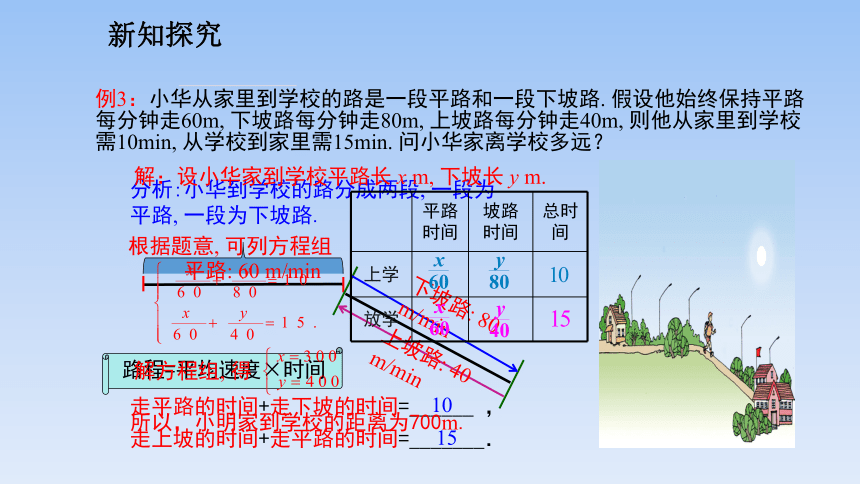
例3:小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m, 下坡路每分钟走80m, 上坡路每分钟走40m, 则他从家里到学校需10min, 从学校到家里需15min. 问小华家离学校多远?
分析:小华到学校的路分成两段, 一段为平路, 一段为下坡路.
平路: 60 m/min
下坡路: 80 m/min
路程=平均速度×时间
走平路的时间+走下坡的时间=______ ,
走上坡的时间+走平路的时间=_______.
10
15
上坡路: 40 m/min
解:设小华家到学校平路长 x m, 下坡长 y m.
根据题意, 可列方程组
解方程组, 得
所以,小明家到学校的距离为700m.
新知探究
平路时间 坡路时间 总时间
上学
放学
新知探究
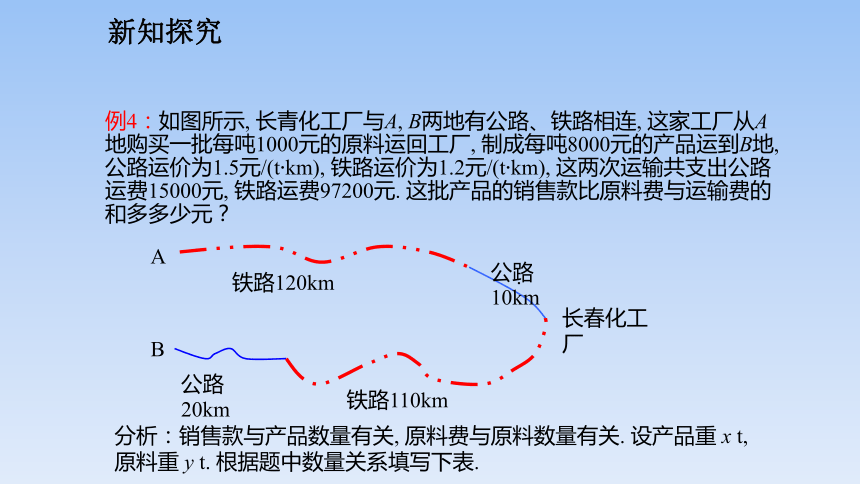
例4:如图所示, 长青化工厂与A, B两地有公路、铁路相连, 这家工厂从A地购买一批每吨1000元的原料运回工厂, 制成每吨8000元的产品运到B地, 公路运价为1.5元/(t?km), 铁路运价为1.2元/(t?km), 这两次运输共支出公路运费15000元, 铁路运费97200元. 这批产品的销售款比原料费与运输费的和多多少元?
分析:销售款与产品数量有关, 原料费与原料数量有关. 设产品重 x t, 原料重 y t. 根据题中数量关系填写下表.
新知探究
1.5×20x
1.5×10y
1.5×(20x+10y)
1.2×110x
1.2×120y
1.2×(110x+120y)
8000x
1000y
由上表, 列方程组
解这个方程组得
因此, 这批产品的销售款比原料费与运输费的和多 元.
1.5×(20x+10y)=15000
1.2×(110x+120y)=97200
1887800
产品 x t 原料 y t 合计
公路运费(元)
铁路运费(元)
价 值(元)
知识归纳
方程组是解决含有多个未知数问题的重要工具, 用方程组解决问题时, 要根据问题中的数量关系列出方程组,理解行程问题和工程问题的数量关系.
例5:一家商店要进行装修, 若请甲、乙两个装修组同时施工, 8天可以完成,
需付两组费用 共3520元; 若先请甲组单独做6天, 再请乙组单独做12天
可完成, 需付两组费用共3480元.
问:(1)甲、乙两组工作一天, 商店应各付多少元?
(2)已知甲组单独做需12天完成, 乙组单独做需24天完成,
单独请哪组, 商店所付费用最少?
(2)单独请甲组需付300×12=3600(元), 单独请乙组需付140×24=3360(元). ∵3600>3360, ∴单独请乙组费用较少.
新知探究
课堂小结
用二元一次方程组解决实际问题
根据问题中的数量关系列出方程组, 理解行程问题和工程问题中的数量关系.
灵活运用, 要仔细分析题意, 找出等量关系,利用它们的数量关系适当地设元, 然后列方程组解题.
课堂小测
1.某体育场的环形跑道长400m, 甲、乙同时从同一起点分别以一定的速度练习长跑. 如果反向而行, 那么他们每隔30s相遇一次. 如果同向而行,那么每隔80s乙就追上甲一次. 甲、乙的速度分别是多少? 设甲的速
度是 x m/s, 乙的速度是 y m/s.则列出的方程组是 .?
课堂小测
解:设飞机的平均速度为 x km/h, 风速为 y km/h. 根据题意得
答: 飞机的平均速度765km/h, 风速为15km/h.
3.某站有甲、乙两辆汽车, 若甲车先出发1h后乙车出发, 则乙车出发
后5h追上甲车; 若甲车先开出30km后乙车出发, 则乙车出发4h后乙车
所走的路程比甲车所走路程多10km. 求两车速度.
解:设甲乙两车的速度分别为 x km/h, y km/h.
根据题意, 得
5y=6x,
4y=4x+40,
解得
答: 甲乙两车的速度分别为50km/h, 60km/h.
课堂小测
4.现要加工400个机器零件, 若甲先做1天, 然后两人再共做2天, 则还有60个未完成; 若两 人齐心合作3天, 则可超产20个. 问甲、乙两人每天各做多少个零件?
课堂小测
课堂小测
5.小明骑摩托车在公路上高速行驶, 12:00时看到里程碑上的数是一个 两位
数, 它的数字之和是7; 13:00时看里程碑上的两位数与12:00时看到的个
位数和十位数颠倒了; 14:00时看到里程碑上的数比12:00时看到的两位数
中间多了个零, 小明在12:00时看到里程碑上的数字是多少?
解:设小明在12:00时看到的数的十位数字是 x, 个位的数字是 y, 则
答: 小明在12:00时看到的数字是16.
第八章
8.3 实际问题与二元一次方程组
8.3.2 用二元一次方程组解决行程、工程等问题
教学目标
1.经历和体验用方程组解决实际问题的过程;(重点)
2.在寻求解决问题的过程中建立适当的方程组模型.(难点)
新课导入
路程=______× ;
工作总量= × .
速度
时间
工作效率
工作时间
解:设甲、乙的速度分别为x km/h, y km/h.
根据题意得
例1: 甲、乙两地相距4km, 以各自的速度同时出发. 如果同向而行, 甲2h追上乙; 如果相向而行, 两人0.5h后相遇. 试问两人的速度各是多少?
解方程组, 得
答:甲的速度为5km/h, 乙的速度为3km/h.
新知探究
新知探究
例2: 悟空顺风探妖踪,
千里只行四分钟.
归时四分行六百,
风速多少才称雄?
顺风速度=悟空行走速度+风速
逆风速度=悟空行走速度-风速
解:设悟空行走速度是每分钟 x里, 风速是每分钟 y里, 则
4(x-y)=600,
x=200,
y=50.
答: 风速是每分钟50里.
4(x+y)=1000,
解得
依题意得
例3:小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m, 下坡路每分钟走80m, 上坡路每分钟走40m, 则他从家里到学校需10min, 从学校到家里需15min. 问小华家离学校多远?
分析:小华到学校的路分成两段, 一段为平路, 一段为下坡路.
平路: 60 m/min
下坡路: 80 m/min
路程=平均速度×时间
走平路的时间+走下坡的时间=______ ,
走上坡的时间+走平路的时间=_______.
10
15
上坡路: 40 m/min
解:设小华家到学校平路长 x m, 下坡长 y m.
根据题意, 可列方程组
解方程组, 得
所以,小明家到学校的距离为700m.
新知探究
平路时间 坡路时间 总时间
上学
放学
新知探究
例4:如图所示, 长青化工厂与A, B两地有公路、铁路相连, 这家工厂从A地购买一批每吨1000元的原料运回工厂, 制成每吨8000元的产品运到B地, 公路运价为1.5元/(t?km), 铁路运价为1.2元/(t?km), 这两次运输共支出公路运费15000元, 铁路运费97200元. 这批产品的销售款比原料费与运输费的和多多少元?
分析:销售款与产品数量有关, 原料费与原料数量有关. 设产品重 x t, 原料重 y t. 根据题中数量关系填写下表.
新知探究
1.5×20x
1.5×10y
1.5×(20x+10y)
1.2×110x
1.2×120y
1.2×(110x+120y)
8000x
1000y
由上表, 列方程组
解这个方程组得
因此, 这批产品的销售款比原料费与运输费的和多 元.
1.5×(20x+10y)=15000
1.2×(110x+120y)=97200
1887800
产品 x t 原料 y t 合计
公路运费(元)
铁路运费(元)
价 值(元)
知识归纳
方程组是解决含有多个未知数问题的重要工具, 用方程组解决问题时, 要根据问题中的数量关系列出方程组,理解行程问题和工程问题的数量关系.
例5:一家商店要进行装修, 若请甲、乙两个装修组同时施工, 8天可以完成,
需付两组费用 共3520元; 若先请甲组单独做6天, 再请乙组单独做12天
可完成, 需付两组费用共3480元.
问:(1)甲、乙两组工作一天, 商店应各付多少元?
(2)已知甲组单独做需12天完成, 乙组单独做需24天完成,
单独请哪组, 商店所付费用最少?
(2)单独请甲组需付300×12=3600(元), 单独请乙组需付140×24=3360(元). ∵3600>3360, ∴单独请乙组费用较少.
新知探究
课堂小结
用二元一次方程组解决实际问题
根据问题中的数量关系列出方程组, 理解行程问题和工程问题中的数量关系.
灵活运用, 要仔细分析题意, 找出等量关系,利用它们的数量关系适当地设元, 然后列方程组解题.
课堂小测
1.某体育场的环形跑道长400m, 甲、乙同时从同一起点分别以一定的速度练习长跑. 如果反向而行, 那么他们每隔30s相遇一次. 如果同向而行,那么每隔80s乙就追上甲一次. 甲、乙的速度分别是多少? 设甲的速
度是 x m/s, 乙的速度是 y m/s.则列出的方程组是 .?
课堂小测
解:设飞机的平均速度为 x km/h, 风速为 y km/h. 根据题意得
答: 飞机的平均速度765km/h, 风速为15km/h.
3.某站有甲、乙两辆汽车, 若甲车先出发1h后乙车出发, 则乙车出发
后5h追上甲车; 若甲车先开出30km后乙车出发, 则乙车出发4h后乙车
所走的路程比甲车所走路程多10km. 求两车速度.
解:设甲乙两车的速度分别为 x km/h, y km/h.
根据题意, 得
5y=6x,
4y=4x+40,
解得
答: 甲乙两车的速度分别为50km/h, 60km/h.
课堂小测
4.现要加工400个机器零件, 若甲先做1天, 然后两人再共做2天, 则还有60个未完成; 若两 人齐心合作3天, 则可超产20个. 问甲、乙两人每天各做多少个零件?
课堂小测
课堂小测
5.小明骑摩托车在公路上高速行驶, 12:00时看到里程碑上的数是一个 两位
数, 它的数字之和是7; 13:00时看里程碑上的两位数与12:00时看到的个
位数和十位数颠倒了; 14:00时看到里程碑上的数比12:00时看到的两位数
中间多了个零, 小明在12:00时看到里程碑上的数字是多少?
解:设小明在12:00时看到的数的十位数字是 x, 个位的数字是 y, 则
答: 小明在12:00时看到的数字是16.
