2019-2020学年青岛新版九年级上册数学《第2章 解直角三角形》单元测试卷(解析版)
文档属性
| 名称 | 2019-2020学年青岛新版九年级上册数学《第2章 解直角三角形》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 529.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 12:57:58 | ||
图片预览



文档简介
2020年青岛新版九年级上册数学《第2章 解直角三角形》单元测试卷
一.选择题(共10小题)
1.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A.2 B.3 C. D.
2.当A为锐角,且<cos∠A<时,∠A的范围是( )
A.0°<∠A<30° B.30°<∠A<60° C.60°<∠A<90° D.30°<∠A<45°
3.如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是,则sinα的值为( )
A. B. C. D.
4.已知:在Rt△ABC中,∠C=90°,sinA=,则cosB的值为( )
A. B. C. D.
5.已知∠A为锐角,且sinA=,那么∠A等于( )
A.15° B.30° C.45° D.60°
6.计算sin20°﹣cos20°的值是(保留四位有效数字)( )
A.﹣0.5976 B.0.5976 C.﹣0.5977 D.0.5977
7.在Rt△ABC中,∠C=90°,如果AC=2,cosA=,那么AB的长是( )
A.3 B. C. D.
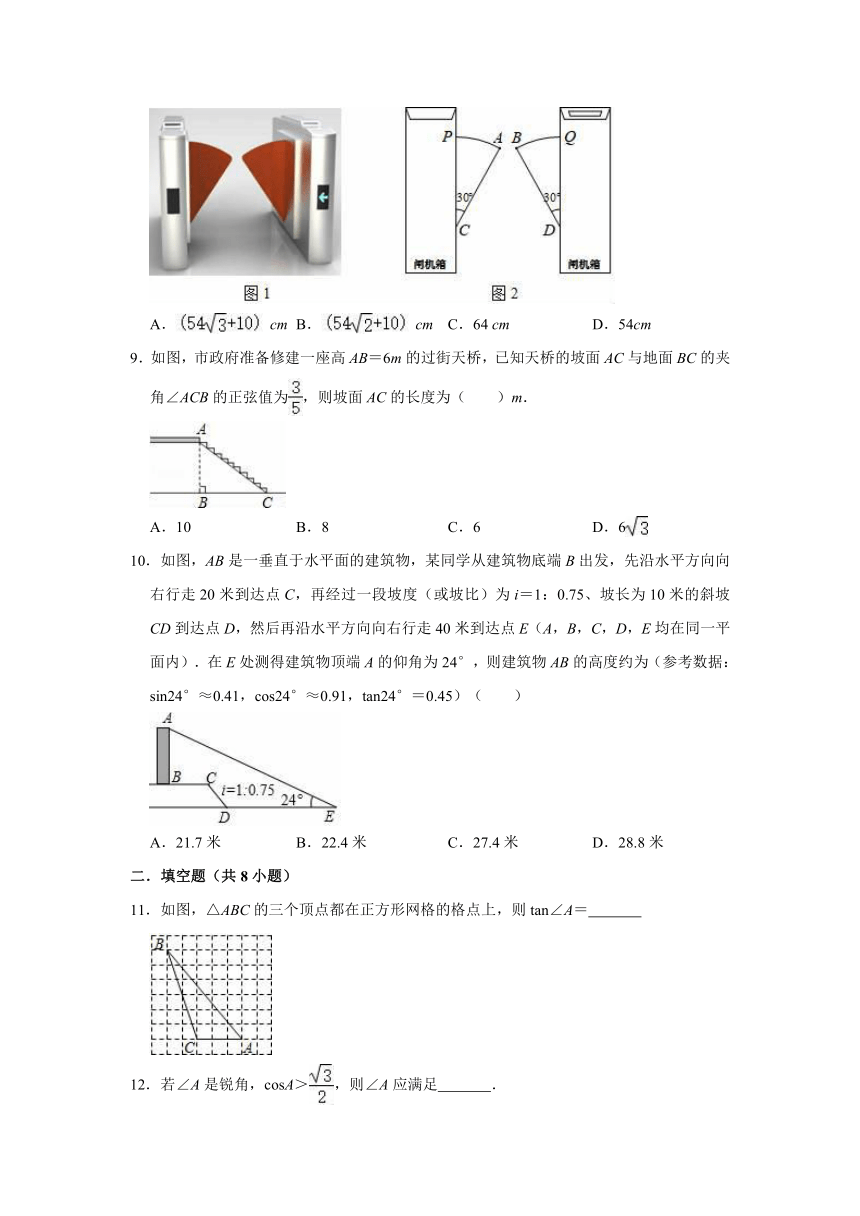
8.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A. cm B. cm C.64 cm D.54cm
9.如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为,则坡面AC的长度为( )m.
A.10 B.8 C.6 D.6
10.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
二.填空题(共8小题)
11.如图,△ABC的三个顶点都在正方形网格的格点上,则tan∠A=
12.若∠A是锐角,cosA>,则∠A应满足 .
13.在Rt△ABC中,∠C=90°,sinA=,则tanA= .
14.在Rt△ABC中,,则cosB的值等于 .
15.已知sinA=,则锐角∠A= .
16.选做题(从下面两题中只选做一题,如果做了两题的,只按第(I)题评分);
(Ⅰ)计算:= .
(Ⅱ)用“>”或“<”号填空: 0.(可用计算器计算)
17.如图,A,B,C是小正方形的顶点,且每个小正方形的边长均为1,则tan∠BAC的值为 .
18.如图是屋架设计图的一部分,立柱BC垂直于横梁AC,BC=4米,∠A=30°,则斜梁AB= 米.
三.解答题(共8小题)
19.在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:=.
20.下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
21.小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=()2+()2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
22.计算: +()﹣1﹣4cos45°﹣()0.
23.如图,△ABC中,∠ACB=90°,sinA=,BC=8,D是AB中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值.
24.如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且.
(1)求钢缆CD的长度;
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
25.如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
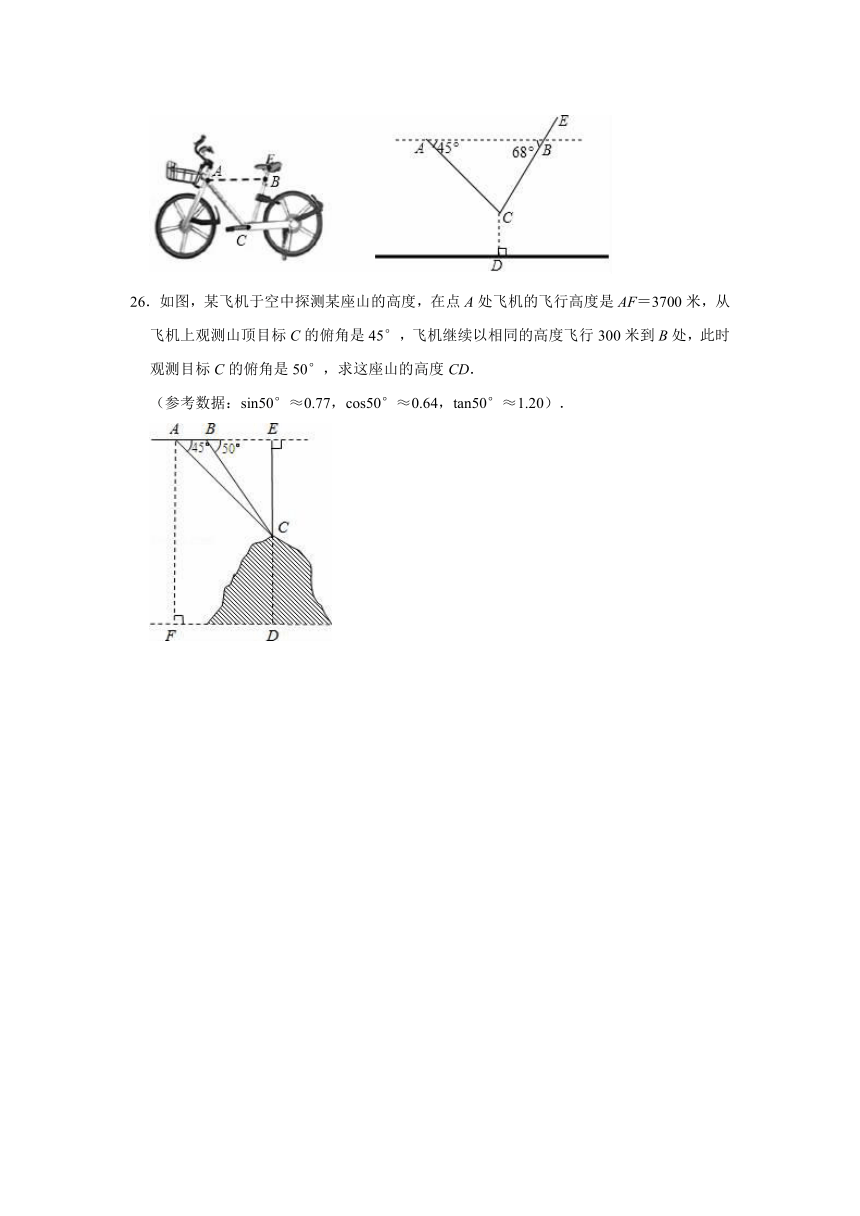
26.如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
2020年青岛新版九年级上册数学《第2章 解直角三角形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A.2 B.3 C. D.
【分析】根据勾股定理求出AC,根据正切的概念计算即可.
【解答】解:设BC=x,则AB=3x,
由勾股定理得,AC==2x,
则tanB==2,
故选:A.
【点评】本题考查的是锐角三角函数的定义以及勾股定理的应用,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
2.当A为锐角,且<cos∠A<时,∠A的范围是( )
A.0°<∠A<30° B.30°<∠A<60° C.60°<∠A<90° D.30°<∠A<45°
【分析】根据锐角的余弦值随着角度的增大而减小进行解答.
【解答】解:∵cos60°=,cos30°=,
∴30°<∠A<60°.
故选:B.
【点评】本题考查了锐角三角函数的增减性,熟记锐角的余弦值随着角度的增大而减小是解题的关键,是基础题,比较简单.
3.如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是,则sinα的值为( )
A. B. C. D.
【分析】过点P作PE⊥x轴于点E,则可得OE=3,PE=m,在Rt△POE中求出OP,继而可得sinα的值.
【解答】解:过点P作PE⊥x轴于点E,
则可得OE=3,PE=m,
在Rt△POE中,tanα==,
解得:m=4,
则OP==5,
故sinα=.
故选:A.
【点评】本题考查了勾股定理及同角的三角函数关系,解答本题的关键是求出OP的长度.
4.已知:在Rt△ABC中,∠C=90°,sinA=,则cosB的值为( )
A. B. C. D.
【分析】根据一个角的正弦等于它余角的余弦,可得答案.
【解答】解:在Rt△ABC中,∠C=90°得
∠B+∠A=90°.
由一个角的正弦等于它余角的余弦,得
cosB=sinA=,
故选:B.
【点评】本题考查了互余两角三角函数的关系,利用一个角的正弦等于它余角的余弦是解题关键.
5.已知∠A为锐角,且sinA=,那么∠A等于( )
A.15° B.30° C.45° D.60°
【分析】根据特殊角的三角函数值求解.
【解答】解:∵sinA=,∠A为锐角,
∴∠A=30°.
故选:B.
【点评】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
6.计算sin20°﹣cos20°的值是(保留四位有效数字)( )
A.﹣0.5976 B.0.5976 C.﹣0.5977 D.0.5977
【分析】本题要求熟练应用计算器,对计算器给出的结果,根据有效数字的概念用四舍五入法取近似数.
【解答】解:按MODE,出现:DEG,按sin20﹣cos20,=后,显示:﹣0.597 7.
故选:C.
【点评】本题考查了熟练应用计算器的能力.
7.在Rt△ABC中,∠C=90°,如果AC=2,cosA=,那么AB的长是( )
A.3 B. C. D.
【分析】根据余弦函数的定义即可直接求解.
【解答】解:∵cosA=,
∴AB=,
故选:A.
【点评】本题考查了余弦函数的定义,是所邻的直角边与斜边的比,理解定义是关键.
8.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A. cm B. cm C.64 cm D.54cm
【分析】过A作AE⊥CP于E,过B作BF⊥DQ于F,则可得AE和BF的长,依据端点A与B之间的距离为10cm,即可得到可以通过闸机的物体的最大宽度.
【解答】解:如图所示,过A作AE⊥CP于E,过B作BF⊥DQ于F,则
Rt△ACE中,AE=AC=×54=27(cm),
同理可得,BF=27cm,
又∵点A与B之间的距离为10cm,
∴通过闸机的物体的最大宽度为27+10+27=64(cm),
故选:C.
【点评】本题主要考查了特殊角的三角函数值,特殊角的三角函数值应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.
9.如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为,则坡面AC的长度为( )m.
A.10 B.8 C.6 D.6
【分析】直接利用锐角三角函数关系得出sinC==,进而得出即可.
【解答】解:∵天桥的坡面AC与地面BC的夹角∠ACB的正弦值为,
∴sinC==,
则=,
解得:AC=10,
则坡面AC的长度为10m.
故选:A.
【点评】此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.
10.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
【分析】作BM⊥ED交ED的延长线于M,CN⊥DM于N.首先解直角三角形Rt△CDN,求出CN,DN,再根据tan24°=,构建方程即可解决问题;
【解答】解:作BM⊥ED交ED的延长线于M,CN⊥DM于N.
在Rt△CDN中,∵==,设CN=4k,DN=3k,
∴CD=10,
∴(3k)2+(4k)2=100,
∴k=2,
∴CN=8,DN=6,
∵四边形BMNC是矩形,
∴BM=CN=8,BC=MN=20,EM=MN+DN+DE=66,
在Rt△AEM中,tan24°=,
∴0.45=,
∴AB=21.7(米),
故选:A.
【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
二.填空题(共8小题)
11.如图,△ABC的三个顶点都在正方形网格的格点上,则tan∠A= 1.2
【分析】作BE⊥AC于E,根据tan∠A=计算即可.
【解答】解:作BE⊥AC于E,则BE=6,AE=5,
∴tan∠A===1.2
故答案为1.2.
【点评】本题考查锐角三角函数的定义,解题的关键是构造直角三角形,记住锐角三角函数的定义,属于中考常考题型.
12.若∠A是锐角,cosA>,则∠A应满足 0°<∠A<30° .
【分析】首先明确cos30°=,再根据余弦函数随角增大而减小,进行分析.
【解答】解:∵cos30°=,余弦函数随角增大而减小,
∴0°<∠A<30°.
【点评】熟记特殊角的三角函数值,了解锐角三角函数的增减性是解题的关键.
13.在Rt△ABC中,∠C=90°,sinA=,则tanA= .
【分析】根据已知条件设出直角三角形一直角边与斜边的长,再根据勾股定理求出另一直角边的长,运用三角函数的定义解答.
【解答】解:由sinA==知,可设a=3x,则c=5x,b=4x.
∴tanA===.
【点评】求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角(或余角)的三角函数关系式求三角函数值.
14.在Rt△ABC中,,则cosB的值等于 .
【分析】根据互余两角的三角函数关系进行解答.
【解答】解:∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
故答案为:.
【点评】本题考查了互余两角的三角函数关系,熟记关系式是解题的关键.
15.已知sinA=,则锐角∠A= 30° .
【分析】根据sin30°=进行解答即可.
【解答】解:∵sinA=,∠A为锐角,
∴∠A=30°.
故答案为:30°.
【点评】本题考查的是特殊角的三角函数值,熟记各特殊角的三角函数值是解答此题的关键.
16.选做题(从下面两题中只选做一题,如果做了两题的,只按第(I)题评分);
(Ⅰ)计算:= .
(Ⅱ)用“>”或“<”号填空: > 0.(可用计算器计算)
【分析】(Ⅰ)sin60°=cos30°=;
(Ⅱ)直接利用计算器计算即可比较.
【解答】解:(Ⅰ)sin60°?cos30°﹣=?﹣=﹣=.
(Ⅱ)sin50°cos40°﹣≈0.0868>0.
故答案为:(Ⅰ).
(Ⅱ)>.
【点评】主要考查了特殊角的三角函数值和计算器的使用.
17.如图,A,B,C是小正方形的顶点,且每个小正方形的边长均为1,则tan∠BAC的值为 1 .
【分析】连接BC,由勾股定理求出AB,BC,AC的长,利用勾股定理的逆定理得到△ABC为等腰直角三角形,即可得出所求.
【解答】解:连接BC,
由网格可得AB=BC==,AC==,
∴AB2+BC2=AC2,
∴△ABC为等腰直角三角形,
∴∠BAC=45°,
则tan∠BAC=1,
故答案为:1.
【点评】此题考查了锐角三角函数的定义,解直角三角形,以及勾股定理,熟练掌握勾股定理是解本题的关键.
18.如图是屋架设计图的一部分,立柱BC垂直于横梁AC,BC=4米,∠A=30°,则斜梁AB= 8 米.
【分析】利用30°所对的直角边等于斜边的一半可求得AB的长.
【解答】解:∵BC⊥AC,BC=4,∠A=30°,
∴AB=2BC=8(米).
【点评】考查的知识点为:直角三角形中,30°所对的直角边等于斜边的一半.
三.解答题(共8小题)
19.在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:=.
【分析】如图,过A作AD⊥BC于D,如果利用三角函数可以分别在△ABD和△ADC中可以得到sinsB,sinC的表达式,由此即可证明题目的结论.
【解答】证明:过A作AD⊥BC于D,
在Rt△ABD中,sinB=,
∴AD=ABsinB,
在Rt△ADC中,sinC=,
∴AD=ACsinC,
∴ABsinB=ACsinC,
而AB=c,AC=b,
∴csinB=bsinC,
∴=.
【点评】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.解题的关键是作辅助线把普通三角形转化为直角三角形解决问题.
20.下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
【分析】(1)利用三角函数的定义和三角形的三边关系得到该结论不成立;
(2)举出反例进行论证.
【解答】解:(1)该不等式不成立,理由如下:
如图,在△ABC中,∠B=90°,∠C=α.
则sinα+cosα=+=>1,故sinα+cosα≤1不成立;
(2)该等式不成立,理由如下:
假设α=30°,则sin2α=sin60°=,2sinα=2sin30°=2×=1,
∵≠1,
∴sin2α≠2sinα,即sin2α=2sinα不成立.
【点评】本题考查了同角三角函数的关系.解题的关键是掌握锐角三角函数的定义和特殊角的三角函数值.
21.小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=()2+()2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
【分析】(1)将α=30°代入,根据三角函数值计算可得;
(2)设∠A=α,则∠B=90°﹣α,根据正弦函数的定义及勾股定理即可验证.
【解答】解:(1)当α=30°时,
sin2α+sin2(90°﹣α)
=sin230°+sin260°
=()2+()2
=+
=1;
(2)小明的猜想成立,证明如下:
如图,在△ABC中,∠C=90°,
设∠A=α,则∠B=90°﹣α,
∴sin2α+sin2(90°﹣α)
=()2+()2
=
=
=1.
【点评】本题主要考查特殊锐角的三角函数值及正弦函数的定义,熟练掌握三角函数的定义及勾股定理是解题的关键.
22.计算: +()﹣1﹣4cos45°﹣()0.
【分析】先根据二次根式的化简、负整数指数幂、特殊角的三角函数值及0指数幂把原式化简,再根据实数混合运算的法则进行计算即可.
【解答】解:原式=2+2﹣4×﹣1,
=2+2﹣2﹣1,
=1.
故答案为:1.
【点评】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂及二次根式等考点的运算.
23.如图,△ABC中,∠ACB=90°,sinA=,BC=8,D是AB中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值.
【分析】(1)在△ABC中根据正弦的定义得到sinA==,则可计算出AB=10,然后根据直角三角形斜边上的中线性质即可得到CD=AB=5;
(2)在Rt△ABC中先利用勾股定理计算出AC=6,在根据三角形面积公式得到S△BDC=S△ADC,则S△BDC=S△ABC,即CD?BE=?AC?BC,于是可计算出BE=,然后在Rt△BDE中利用余弦的定义求解.
【解答】解:(1)在△ABC中,∵∠ACB=90°,
∴sinA==,
而BC=8,
∴AB=10,
∵D是AB中点,
∴CD=AB=5;
(2)在Rt△ABC中,∵AB=10,BC=8,
∴AC==6,
∵D是AB中点,
∴BD=5,S△BDC=S△ADC,
∴S△BDC=S△ABC,即CD?BE=?AC?BC,
∴BE==,
在Rt△BDE中,cos∠DBE===,
即cos∠ABE的值为.
【点评】本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了直角三角形斜边上的中线性质和三角形面积公式.
24.如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且.
(1)求钢缆CD的长度;
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
【分析】(1)根据三角函数可求得CD;
(2)过点E作EF⊥AB于点F.由∠EAB=120°,得∠EAF=60°,再根据三角函数求得AF,从而得出答案.
【解答】解:(1)在Rt△DCB中,sin∠DCB==,
∴设DB=4x,DC=5x,
∴(4x)2+25=(5x)2,
解得,
∴CD=米,DB=米.
(2)如图,过点E作EF⊥AB于点F.
∵∠EAB=120°,∴∠EAF=60°,
∴AF=AE?cos∠EAF=1.6×=0.8(米),
∴FB=AF+AD+DB=0.8+2+=(米).
∴灯的顶端E距离地面米.
【点评】本题考查了解直角三角形的应用,运用三角函数可得出答案.
25.如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
【分析】过点C作CH⊥AB于点H,过点E作EF垂直于AB延长线于点F,设CH=x,则AH=CH=x,BH=CHcot68°=0.4x,由AB=49知x+0.4x=49,解之求得CH的长,再由EF=BEsin68°=3.72根据点E到地面的距离为CH+CD+EF可得答案.
【解答】解:过点C作CH⊥AB于点H,过点E作EF垂直于AB延长线于点F,
设CH=x,则AH=CH=x,BH=CHcot68°=0.4x,
由AB=49知x+0.4x=49,
解得:x=35,
∵BE=4,
∴EF=BEsin68°=3.72,
则点E到地面的距离为CH+CD+EF=35+28+3.72≈66.7(cm),
答:点E到地面的距离约为66.7cm.
【点评】本题主要考查解直角三角形的应用﹣坡度坡角问题,解题的关键是理解题意构建直角三角形并熟练掌握三角函数的定义.
26.如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
【分析】设EC=x,则在RT△BCE中,可表示出BE,在Rt△ACE中,可表示出AE,继而根据AB+BE=AE,可得出方程,解出即可得出答案.
【解答】解:设EC=x,
在Rt△BCE中,tan∠EBC=,
则BE==x,
在Rt△ACE中,tan∠EAC=,
则AE==x,
∵AB+BE=AE,
∴300+x=x,
解得:x=1800,
这座山的高度CD=DE﹣EC=3700﹣1800=1900(米).
答:这座山的高度是1900米.
【点评】此题考查了解直角三角形的应用,解答本题的关键是两次利用三角函数的知识,求出BE及AE的表达式,属于基础题,要能将实际问题转化为数学计算.
一.选择题(共10小题)
1.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A.2 B.3 C. D.
2.当A为锐角,且<cos∠A<时,∠A的范围是( )
A.0°<∠A<30° B.30°<∠A<60° C.60°<∠A<90° D.30°<∠A<45°
3.如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是,则sinα的值为( )
A. B. C. D.
4.已知:在Rt△ABC中,∠C=90°,sinA=,则cosB的值为( )
A. B. C. D.
5.已知∠A为锐角,且sinA=,那么∠A等于( )
A.15° B.30° C.45° D.60°
6.计算sin20°﹣cos20°的值是(保留四位有效数字)( )
A.﹣0.5976 B.0.5976 C.﹣0.5977 D.0.5977
7.在Rt△ABC中,∠C=90°,如果AC=2,cosA=,那么AB的长是( )
A.3 B. C. D.
8.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A. cm B. cm C.64 cm D.54cm
9.如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为,则坡面AC的长度为( )m.
A.10 B.8 C.6 D.6
10.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
二.填空题(共8小题)
11.如图,△ABC的三个顶点都在正方形网格的格点上,则tan∠A=
12.若∠A是锐角,cosA>,则∠A应满足 .
13.在Rt△ABC中,∠C=90°,sinA=,则tanA= .
14.在Rt△ABC中,,则cosB的值等于 .
15.已知sinA=,则锐角∠A= .
16.选做题(从下面两题中只选做一题,如果做了两题的,只按第(I)题评分);
(Ⅰ)计算:= .
(Ⅱ)用“>”或“<”号填空: 0.(可用计算器计算)
17.如图,A,B,C是小正方形的顶点,且每个小正方形的边长均为1,则tan∠BAC的值为 .
18.如图是屋架设计图的一部分,立柱BC垂直于横梁AC,BC=4米,∠A=30°,则斜梁AB= 米.
三.解答题(共8小题)
19.在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:=.
20.下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
21.小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=()2+()2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
22.计算: +()﹣1﹣4cos45°﹣()0.
23.如图,△ABC中,∠ACB=90°,sinA=,BC=8,D是AB中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值.
24.如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且.
(1)求钢缆CD的长度;
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
25.如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
26.如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
2020年青岛新版九年级上册数学《第2章 解直角三角形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.在Rt△ABC中,∠C=90°,若斜边AB是直角边BC的3倍,则tanB的值是( )
A.2 B.3 C. D.
【分析】根据勾股定理求出AC,根据正切的概念计算即可.
【解答】解:设BC=x,则AB=3x,
由勾股定理得,AC==2x,
则tanB==2,
故选:A.
【点评】本题考查的是锐角三角函数的定义以及勾股定理的应用,在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.
2.当A为锐角,且<cos∠A<时,∠A的范围是( )
A.0°<∠A<30° B.30°<∠A<60° C.60°<∠A<90° D.30°<∠A<45°
【分析】根据锐角的余弦值随着角度的增大而减小进行解答.
【解答】解:∵cos60°=,cos30°=,
∴30°<∠A<60°.
故选:B.
【点评】本题考查了锐角三角函数的增减性,熟记锐角的余弦值随着角度的增大而减小是解题的关键,是基础题,比较简单.
3.如图,在直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是,则sinα的值为( )
A. B. C. D.
【分析】过点P作PE⊥x轴于点E,则可得OE=3,PE=m,在Rt△POE中求出OP,继而可得sinα的值.
【解答】解:过点P作PE⊥x轴于点E,
则可得OE=3,PE=m,
在Rt△POE中,tanα==,
解得:m=4,
则OP==5,
故sinα=.
故选:A.
【点评】本题考查了勾股定理及同角的三角函数关系,解答本题的关键是求出OP的长度.
4.已知:在Rt△ABC中,∠C=90°,sinA=,则cosB的值为( )
A. B. C. D.
【分析】根据一个角的正弦等于它余角的余弦,可得答案.
【解答】解:在Rt△ABC中,∠C=90°得
∠B+∠A=90°.
由一个角的正弦等于它余角的余弦,得
cosB=sinA=,
故选:B.
【点评】本题考查了互余两角三角函数的关系,利用一个角的正弦等于它余角的余弦是解题关键.
5.已知∠A为锐角,且sinA=,那么∠A等于( )
A.15° B.30° C.45° D.60°
【分析】根据特殊角的三角函数值求解.
【解答】解:∵sinA=,∠A为锐角,
∴∠A=30°.
故选:B.
【点评】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.
6.计算sin20°﹣cos20°的值是(保留四位有效数字)( )
A.﹣0.5976 B.0.5976 C.﹣0.5977 D.0.5977
【分析】本题要求熟练应用计算器,对计算器给出的结果,根据有效数字的概念用四舍五入法取近似数.
【解答】解:按MODE,出现:DEG,按sin20﹣cos20,=后,显示:﹣0.597 7.
故选:C.
【点评】本题考查了熟练应用计算器的能力.
7.在Rt△ABC中,∠C=90°,如果AC=2,cosA=,那么AB的长是( )
A.3 B. C. D.
【分析】根据余弦函数的定义即可直接求解.
【解答】解:∵cosA=,
∴AB=,
故选:A.
【点评】本题考查了余弦函数的定义,是所邻的直角边与斜边的比,理解定义是关键.
8.图1是一个地铁站入口的双翼闸机.如图2,它的双翼展开时,双翼边缘的端点A与B之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°.当双翼收起时,可以通过闸机的物体的最大宽度为( )
A. cm B. cm C.64 cm D.54cm
【分析】过A作AE⊥CP于E,过B作BF⊥DQ于F,则可得AE和BF的长,依据端点A与B之间的距离为10cm,即可得到可以通过闸机的物体的最大宽度.
【解答】解:如图所示,过A作AE⊥CP于E,过B作BF⊥DQ于F,则
Rt△ACE中,AE=AC=×54=27(cm),
同理可得,BF=27cm,
又∵点A与B之间的距离为10cm,
∴通过闸机的物体的最大宽度为27+10+27=64(cm),
故选:C.
【点评】本题主要考查了特殊角的三角函数值,特殊角的三角函数值应用广泛,一是它可以当作数进行运算,二是具有三角函数的特点,在解直角三角形中应用较多.
9.如图,市政府准备修建一座高AB=6m的过街天桥,已知天桥的坡面AC与地面BC的夹角∠ACB的正弦值为,则坡面AC的长度为( )m.
A.10 B.8 C.6 D.6
【分析】直接利用锐角三角函数关系得出sinC==,进而得出即可.
【解答】解:∵天桥的坡面AC与地面BC的夹角∠ACB的正弦值为,
∴sinC==,
则=,
解得:AC=10,
则坡面AC的长度为10m.
故选:A.
【点评】此题主要考查了解直角三角形的应用,熟练应用锐角三角函数关系是解题关键.
10.如图,AB是一垂直于水平面的建筑物,某同学从建筑物底端B出发,先沿水平方向向右行走20米到达点C,再经过一段坡度(或坡比)为i=1:0.75、坡长为10米的斜坡CD到达点D,然后再沿水平方向向右行走40米到达点E(A,B,C,D,E均在同一平面内).在E处测得建筑物顶端A的仰角为24°,则建筑物AB的高度约为(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°=0.45)( )
A.21.7米 B.22.4米 C.27.4米 D.28.8米
【分析】作BM⊥ED交ED的延长线于M,CN⊥DM于N.首先解直角三角形Rt△CDN,求出CN,DN,再根据tan24°=,构建方程即可解决问题;
【解答】解:作BM⊥ED交ED的延长线于M,CN⊥DM于N.
在Rt△CDN中,∵==,设CN=4k,DN=3k,
∴CD=10,
∴(3k)2+(4k)2=100,
∴k=2,
∴CN=8,DN=6,
∵四边形BMNC是矩形,
∴BM=CN=8,BC=MN=20,EM=MN+DN+DE=66,
在Rt△AEM中,tan24°=,
∴0.45=,
∴AB=21.7(米),
故选:A.
【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.
二.填空题(共8小题)
11.如图,△ABC的三个顶点都在正方形网格的格点上,则tan∠A= 1.2
【分析】作BE⊥AC于E,根据tan∠A=计算即可.
【解答】解:作BE⊥AC于E,则BE=6,AE=5,
∴tan∠A===1.2
故答案为1.2.
【点评】本题考查锐角三角函数的定义,解题的关键是构造直角三角形,记住锐角三角函数的定义,属于中考常考题型.
12.若∠A是锐角,cosA>,则∠A应满足 0°<∠A<30° .
【分析】首先明确cos30°=,再根据余弦函数随角增大而减小,进行分析.
【解答】解:∵cos30°=,余弦函数随角增大而减小,
∴0°<∠A<30°.
【点评】熟记特殊角的三角函数值,了解锐角三角函数的增减性是解题的关键.
13.在Rt△ABC中,∠C=90°,sinA=,则tanA= .
【分析】根据已知条件设出直角三角形一直角边与斜边的长,再根据勾股定理求出另一直角边的长,运用三角函数的定义解答.
【解答】解:由sinA==知,可设a=3x,则c=5x,b=4x.
∴tanA===.
【点评】求锐角的三角函数值的方法:利用锐角三角函数的定义,通过设参数的方法求三角函数值,或者利用同角(或余角)的三角函数关系式求三角函数值.
14.在Rt△ABC中,,则cosB的值等于 .
【分析】根据互余两角的三角函数关系进行解答.
【解答】解:∵∠C=90°,
∴∠A+∠B=90°,
∴cosB=sinA,
∵sinA=,
∴cosB=.
故答案为:.
【点评】本题考查了互余两角的三角函数关系,熟记关系式是解题的关键.
15.已知sinA=,则锐角∠A= 30° .
【分析】根据sin30°=进行解答即可.
【解答】解:∵sinA=,∠A为锐角,
∴∠A=30°.
故答案为:30°.
【点评】本题考查的是特殊角的三角函数值,熟记各特殊角的三角函数值是解答此题的关键.
16.选做题(从下面两题中只选做一题,如果做了两题的,只按第(I)题评分);
(Ⅰ)计算:= .
(Ⅱ)用“>”或“<”号填空: > 0.(可用计算器计算)
【分析】(Ⅰ)sin60°=cos30°=;
(Ⅱ)直接利用计算器计算即可比较.
【解答】解:(Ⅰ)sin60°?cos30°﹣=?﹣=﹣=.
(Ⅱ)sin50°cos40°﹣≈0.0868>0.
故答案为:(Ⅰ).
(Ⅱ)>.
【点评】主要考查了特殊角的三角函数值和计算器的使用.
17.如图,A,B,C是小正方形的顶点,且每个小正方形的边长均为1,则tan∠BAC的值为 1 .
【分析】连接BC,由勾股定理求出AB,BC,AC的长,利用勾股定理的逆定理得到△ABC为等腰直角三角形,即可得出所求.
【解答】解:连接BC,
由网格可得AB=BC==,AC==,
∴AB2+BC2=AC2,
∴△ABC为等腰直角三角形,
∴∠BAC=45°,
则tan∠BAC=1,
故答案为:1.
【点评】此题考查了锐角三角函数的定义,解直角三角形,以及勾股定理,熟练掌握勾股定理是解本题的关键.
18.如图是屋架设计图的一部分,立柱BC垂直于横梁AC,BC=4米,∠A=30°,则斜梁AB= 8 米.
【分析】利用30°所对的直角边等于斜边的一半可求得AB的长.
【解答】解:∵BC⊥AC,BC=4,∠A=30°,
∴AB=2BC=8(米).
【点评】考查的知识点为:直角三角形中,30°所对的直角边等于斜边的一半.
三.解答题(共8小题)
19.在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:=.
【分析】如图,过A作AD⊥BC于D,如果利用三角函数可以分别在△ABD和△ADC中可以得到sinsB,sinC的表达式,由此即可证明题目的结论.
【解答】证明:过A作AD⊥BC于D,
在Rt△ABD中,sinB=,
∴AD=ABsinB,
在Rt△ADC中,sinC=,
∴AD=ACsinC,
∴ABsinB=ACsinC,
而AB=c,AC=b,
∴csinB=bsinC,
∴=.
【点评】本题考查锐角三角函数的定义及运用:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.解题的关键是作辅助线把普通三角形转化为直角三角形解决问题.
20.下列关系式是否成立(0<α<90°),请说明理由.
(1)sinα+cosα≤1;
(2)sin2α=2sinα.
【分析】(1)利用三角函数的定义和三角形的三边关系得到该结论不成立;
(2)举出反例进行论证.
【解答】解:(1)该不等式不成立,理由如下:
如图,在△ABC中,∠B=90°,∠C=α.
则sinα+cosα=+=>1,故sinα+cosα≤1不成立;
(2)该等式不成立,理由如下:
假设α=30°,则sin2α=sin60°=,2sinα=2sin30°=2×=1,
∵≠1,
∴sin2α≠2sinα,即sin2α=2sinα不成立.
【点评】本题考查了同角三角函数的关系.解题的关键是掌握锐角三角函数的定义和特殊角的三角函数值.
21.小明在某次作业中得到如下结果:
sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=()2+()2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.
【分析】(1)将α=30°代入,根据三角函数值计算可得;
(2)设∠A=α,则∠B=90°﹣α,根据正弦函数的定义及勾股定理即可验证.
【解答】解:(1)当α=30°时,
sin2α+sin2(90°﹣α)
=sin230°+sin260°
=()2+()2
=+
=1;
(2)小明的猜想成立,证明如下:
如图,在△ABC中,∠C=90°,
设∠A=α,则∠B=90°﹣α,
∴sin2α+sin2(90°﹣α)
=()2+()2
=
=
=1.
【点评】本题主要考查特殊锐角的三角函数值及正弦函数的定义,熟练掌握三角函数的定义及勾股定理是解题的关键.
22.计算: +()﹣1﹣4cos45°﹣()0.
【分析】先根据二次根式的化简、负整数指数幂、特殊角的三角函数值及0指数幂把原式化简,再根据实数混合运算的法则进行计算即可.
【解答】解:原式=2+2﹣4×﹣1,
=2+2﹣2﹣1,
=1.
故答案为:1.
【点评】本题考查实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟记特殊角的三角函数值,熟练掌握负整数指数幂、零指数幂及二次根式等考点的运算.
23.如图,△ABC中,∠ACB=90°,sinA=,BC=8,D是AB中点,过点B作直线CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值.
【分析】(1)在△ABC中根据正弦的定义得到sinA==,则可计算出AB=10,然后根据直角三角形斜边上的中线性质即可得到CD=AB=5;
(2)在Rt△ABC中先利用勾股定理计算出AC=6,在根据三角形面积公式得到S△BDC=S△ADC,则S△BDC=S△ABC,即CD?BE=?AC?BC,于是可计算出BE=,然后在Rt△BDE中利用余弦的定义求解.
【解答】解:(1)在△ABC中,∵∠ACB=90°,
∴sinA==,
而BC=8,
∴AB=10,
∵D是AB中点,
∴CD=AB=5;
(2)在Rt△ABC中,∵AB=10,BC=8,
∴AC==6,
∵D是AB中点,
∴BD=5,S△BDC=S△ADC,
∴S△BDC=S△ABC,即CD?BE=?AC?BC,
∴BE==,
在Rt△BDE中,cos∠DBE===,
即cos∠ABE的值为.
【点评】本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.也考查了直角三角形斜边上的中线性质和三角形面积公式.
24.如图,某中心广场灯柱AB被钢缆CD固定,已知CB=5米,且.
(1)求钢缆CD的长度;
(2)若AD=2米,灯的顶端E距离A处1.6米,且∠EAB=120°,则灯的顶端E距离地面多少米?
【分析】(1)根据三角函数可求得CD;
(2)过点E作EF⊥AB于点F.由∠EAB=120°,得∠EAF=60°,再根据三角函数求得AF,从而得出答案.
【解答】解:(1)在Rt△DCB中,sin∠DCB==,
∴设DB=4x,DC=5x,
∴(4x)2+25=(5x)2,
解得,
∴CD=米,DB=米.
(2)如图,过点E作EF⊥AB于点F.
∵∠EAB=120°,∴∠EAF=60°,
∴AF=AE?cos∠EAF=1.6×=0.8(米),
∴FB=AF+AD+DB=0.8+2+=(米).
∴灯的顶端E距离地面米.
【点评】本题考查了解直角三角形的应用,运用三角函数可得出答案.
25.如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
【分析】过点C作CH⊥AB于点H,过点E作EF垂直于AB延长线于点F,设CH=x,则AH=CH=x,BH=CHcot68°=0.4x,由AB=49知x+0.4x=49,解之求得CH的长,再由EF=BEsin68°=3.72根据点E到地面的距离为CH+CD+EF可得答案.
【解答】解:过点C作CH⊥AB于点H,过点E作EF垂直于AB延长线于点F,
设CH=x,则AH=CH=x,BH=CHcot68°=0.4x,
由AB=49知x+0.4x=49,
解得:x=35,
∵BE=4,
∴EF=BEsin68°=3.72,
则点E到地面的距离为CH+CD+EF=35+28+3.72≈66.7(cm),
答:点E到地面的距离约为66.7cm.
【点评】本题主要考查解直角三角形的应用﹣坡度坡角问题,解题的关键是理解题意构建直角三角形并熟练掌握三角函数的定义.
26.如图,某飞机于空中探测某座山的高度,在点A处飞机的飞行高度是AF=3700米,从飞机上观测山顶目标C的俯角是45°,飞机继续以相同的高度飞行300米到B处,此时观测目标C的俯角是50°,求这座山的高度CD.
(参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.20).
【分析】设EC=x,则在RT△BCE中,可表示出BE,在Rt△ACE中,可表示出AE,继而根据AB+BE=AE,可得出方程,解出即可得出答案.
【解答】解:设EC=x,
在Rt△BCE中,tan∠EBC=,
则BE==x,
在Rt△ACE中,tan∠EAC=,
则AE==x,
∵AB+BE=AE,
∴300+x=x,
解得:x=1800,
这座山的高度CD=DE﹣EC=3700﹣1800=1900(米).
答:这座山的高度是1900米.
【点评】此题考查了解直角三角形的应用,解答本题的关键是两次利用三角函数的知识,求出BE及AE的表达式,属于基础题,要能将实际问题转化为数学计算.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
