2019-2020学年青岛新版上册数学八年级《第4章 数据分析》单元测试卷(解析版)
文档属性
| 名称 | 2019-2020学年青岛新版上册数学八年级《第4章 数据分析》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 414.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 13:28:21 | ||
图片预览



文档简介
2020年青岛新版上册数学八年级《第4章 数据分析》单元测试卷
一.选择题(共10小题)
1.某班抽取6名同学进行体育达标测试,成绩如下:80,90,75,80,75,80.下列关于对这组数据的描述错误的是( )
A.众数是80 B.平均数是80 C.中位数是75 D.极差是15
2.一组数据2,3,5,7,8的平均数是( )
A.2 B.3 C.4 D.5
3.甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元,若将甲种8千克,乙种10千克,丙种3千克混在一起,则售价应定为每千克( )
A.7元 B.6.8元 C.7.5元 D.8.6元
4.有8个数的平均数是11,另外有12个数的平均数是12,这20个数的平均数是( )
A.11.6 B.2.32 C.23.2 D.11.5
5.5个相异自然数的平均数为12,中位数为17,这5个自然数中最大一个的可能值的最大值是( )
A.21 B.22 C.23 D.24
6.一组数据2,2,2,4,4,7的中位数是( )
A.2 B.3 C.4 D.7
7.某男子排球队20名队员的身高如表:
身高(cm) 180 186 188 192 208
人数(个) 4 6 5 3 2
则此男子排球队20名队员的身高的众数和中位数分别是(单位:cm)( )
A.186,186 B.186,187 C.208,188 D.188,187
8.一组数据:2,﹣1,0,3,﹣3,2.则这组数据的中位数和众数分别是( )
A.0,2 B.1.5,2 C.1,2 D.1,3
9.在10,20,40,30,80,90,50,40,40,50这10个数据中,算出这组数据的极差是( )
A.40 B.70 C.80 D.90
10.为了帮助本市一名患病的高中生,某班15名同学积极捐款,他们捐款数额如表:
捐款的数额(单位:元) 5 10 20 50 100
人数(单位:人) 2 4 5 3 1
关于这15名同学所捐款的数额,下列说法正确的是( )
A.众数是100 B.中位数是30 C.极差是20 D.中位数是20
二.填空题(共8小题)
11.某市2007年5月份某一周的日最高气温(单位:℃)分别为:25,28,30,29,31,32,28,这周的日最高气温的平均值是 .
12.超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
测试项目 创新能力 综合知识 语言表达
测试成绩(分数) 70 80 90
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是 分.
13.某同学用计算器求30个数据的平均数时,错将其中的一个数据105输入成15,则由此求出的平均数与实际平均数的差是 .
14.已知一组数据是3,4,7,a,中位数为4,则a= .
15.某中学随机调查了15名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
一周在校的体育锻炼时间(小时) 5 6 7 8
人数 2 5 6 2
那么这15名学生这一周在校参加体育锻炼的时间的众数是 小时.
16.数据﹣5,6,4,0,1,7,5的极差为 .
17.甲、乙两人在相同的情况下各打靶10次,打靶的成绩如图,这两人10次打靶平均命中环数都为7环,则S2甲 S2乙(填“>”、“<”或“=”).
18.一组数据:1,3,2,5,x的平均数为3,那么x= ,这组数据的标准差是 .
三.解答题(共8小题)
19.下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
考试类别 平时 期中考试 期末考试
第一单元 第二单元 第三单元 第四单元
成绩 88 86 90 92 90 96
(1)李刚同学6次成绩的极差是 .
(2)李刚同学6次成绩的中位数是 .
(3)李刚同学平时成绩的平均数是 .
(4)如果用下图的权重给李刚打分,他应该得多少分?(满分100分,写出解题过程)
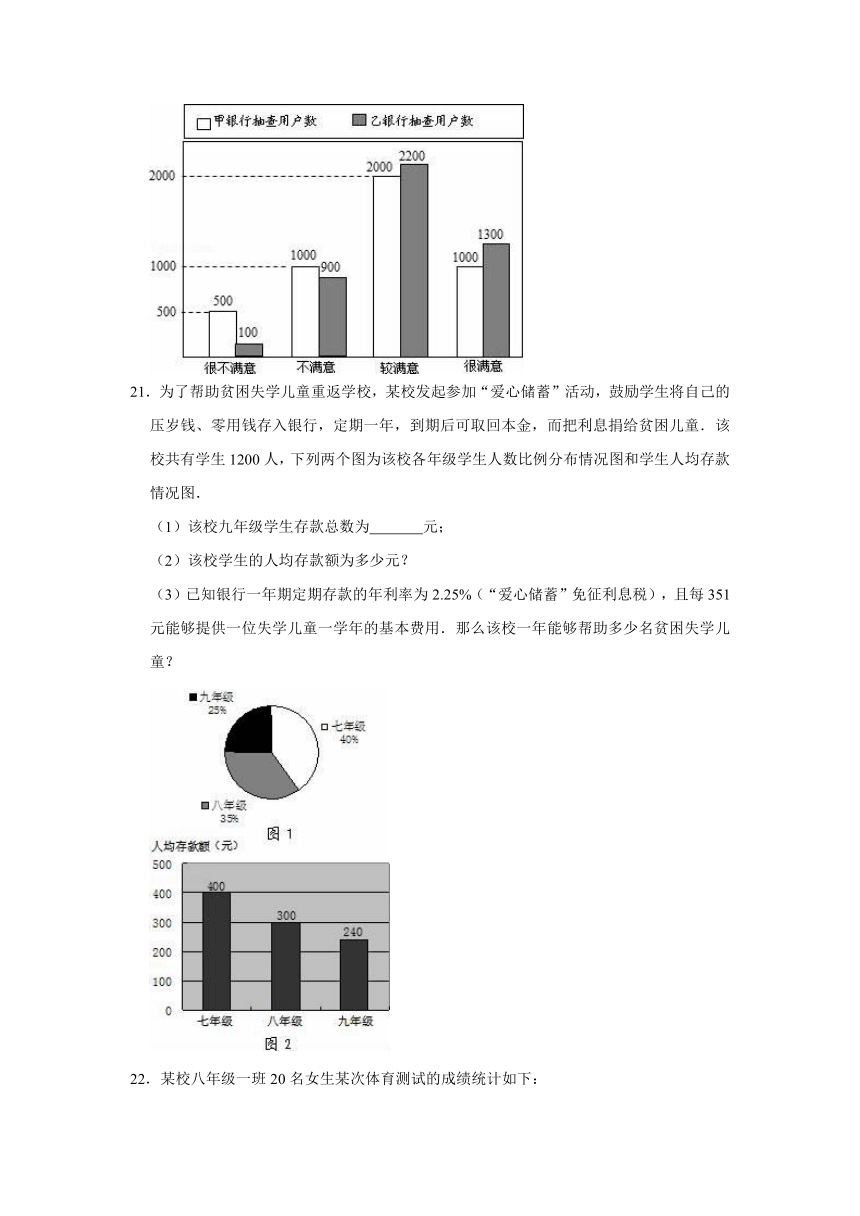
20.年终将至,上级管理部门对甲、乙两个银行的服务情况进行了抽查.如图反映了被抽查对象对两个银行服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为0分、1分、2分、4分.
(1)请问:甲银行的用户满意度分数的众数为 ,乙银行的用户满意度分数的中位数为 ;
(2)分别求出甲、乙两银行的用户满意度分数的平均值;
(3)请你根据所学的统计知识,判断哪个银行的用户满意度较高,并简要说明理由.
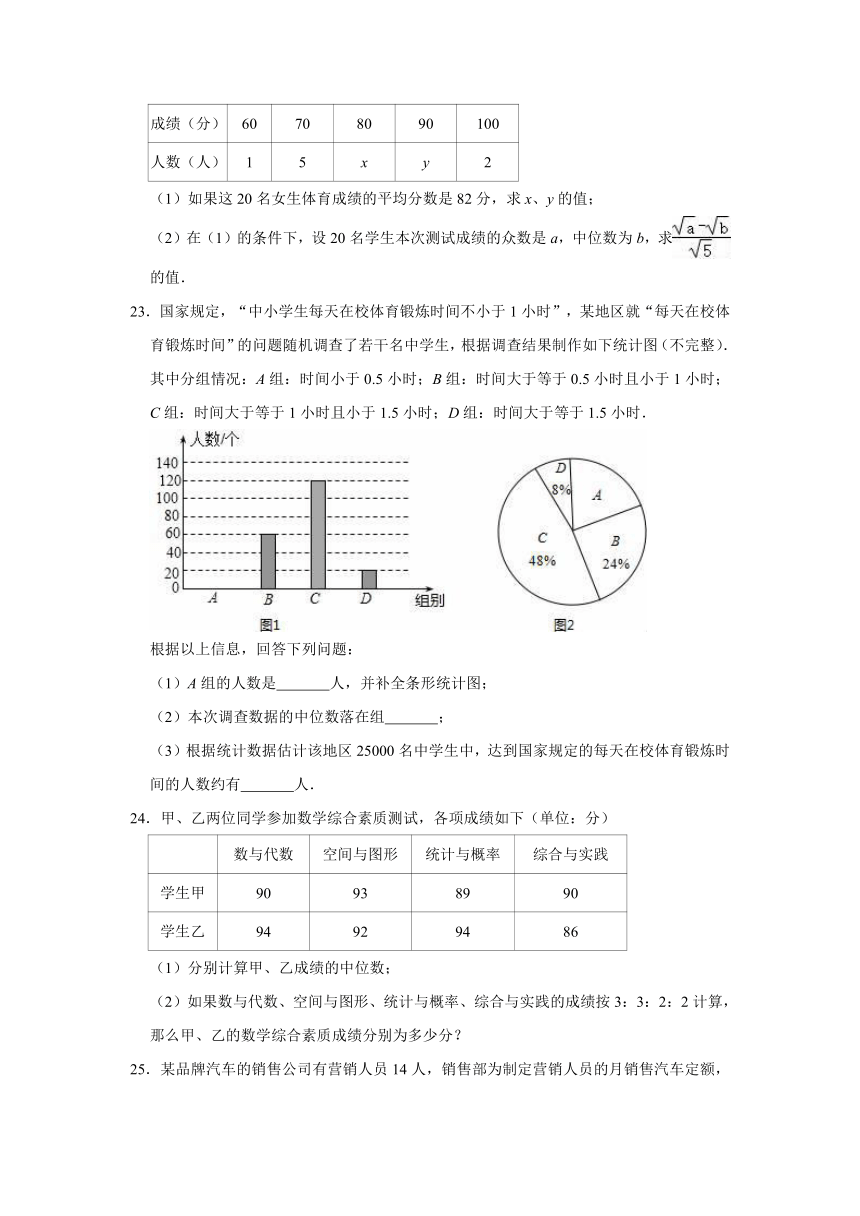
21.为了帮助贫困失学儿童重返学校,某校发起参加“爱心储蓄”活动,鼓励学生将自己的压岁钱、零用钱存入银行,定期一年,到期后可取回本金,而把利息捐给贫困儿童.该校共有学生1200人,下列两个图为该校各年级学生人数比例分布情况图和学生人均存款情况图.
(1)该校九年级学生存款总数为 元;
(2)该校学生的人均存款额为多少元?
(3)已知银行一年期定期存款的年利率为2.25%(“爱心储蓄”免征利息税),且每351元能够提供一位失学儿童一学年的基本费用.那么该校一年能够帮助多少名贫困失学儿童?
22.某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生本次测试成绩的众数是a,中位数为b,求的值.
23.国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有 人.
24.甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 空间与图形 统计与概率 综合与实践
学生甲 90 93 89 90
学生乙 94 92 94 86
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
25.某品牌汽车的销售公司有营销人员14人,销售部为制定营销人员的月销售汽车定额,统计了这14人在某月的销售量如下表:
销售辆数 20 17 13 8 5 4
人 数 1 1 2 5 3 2
(1)这14位销售员该月销售某品牌汽车的平均数、众数和中位数各是多少辆?
(2)销售部经理把每位销售员每月销售汽车定额为9辆,你认为是否合理?为什么?如果不合理,请你设计一个比较合理的销售定额,并说明理由.
26.在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有 人;
(2)补全下表中空缺的三个统计量:
平均数(分) 中位数(分) 众数(分)
一班 77.6 80
二班 90
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.
2020年青岛新版上册数学八年级《第4章 数据分析》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.某班抽取6名同学进行体育达标测试,成绩如下:80,90,75,80,75,80.下列关于对这组数据的描述错误的是( )
A.众数是80 B.平均数是80 C.中位数是75 D.极差是15
【分析】根据平均数,中位数,众数及极差的概念进行判断.
【解答】解:将6名同学的成绩从小到大排列,第3、4个数都是80,故中位数是80,
∴答案C是错误的.
故选:C.
【点评】本题重点考查平均数,中位数,众数及极差的概念及其求法.
2.一组数据2,3,5,7,8的平均数是( )
A.2 B.3 C.4 D.5
【分析】根据平均数的定义计算.
【解答】解:数据2,3,5,7,8的平均数==5.
故选:D.
【点评】本题考查了平均数:平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.
3.甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元,若将甲种8千克,乙种10千克,丙种3千克混在一起,则售价应定为每千克( )
A.7元 B.6.8元 C.7.5元 D.8.6元
【分析】根据加权平均数的计算方法:先求出所有糖果的总钱数,再除以糖果的总质量,即可得出答案.
【解答】解:售价应定为:≈6.8(元);
故选:B.
【点评】本题考查的是加权平均数的求法.本题易出现的错误是对加权平均数的理解不正确,而求6、7、8这三个数的平均数.
4.有8个数的平均数是11,另外有12个数的平均数是12,这20个数的平均数是( )
A.11.6 B.2.32 C.23.2 D.11.5
【分析】根据平均数的公式求解即可,8个数的和加12个数的和除以20即可.
【解答】解:根据平均数的求法:共(8+12)=20个数,这些数之和为8×11+12×12=232,故这些数的平均数是=11.6.
故选:A.
【点评】本题考查的是样本平均数的求法..
5.5个相异自然数的平均数为12,中位数为17,这5个自然数中最大一个的可能值的最大值是( )
A.21 B.22 C.23 D.24
【分析】根据5个相异自然数的平均数为12,得到5个自然数的和,又因为中位数为17,求数据中的最大数,所以可得出这组数据,即可求得这5个自然数中最大一个的值.
【解答】解:∵5个相异自然数的平均数为12
∴5个相异自然数的和为60;
∵中位数为17,
∴这5个数中有2个数比17小,有两个数比17大;
又∵求这5个数中的最大一个的可能值的最大值,
∴设这5个数中两个最小的数为0和1,而比17大的最小的自然数是18,
∴剩下的第5个数是:60﹣0﹣1﹣17﹣18=24,即第5个数是24,
∴这5个数为0,1,17,18,24.
∴这5个自然数中最大一个的可能值的最大值是24;
故选:D.
【点评】考查中位数和平均数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
6.一组数据2,2,2,4,4,7的中位数是( )
A.2 B.3 C.4 D.7
【分析】中位数是指将一组数据按大小顺序排列后,处在最中间的一个数(或处在最中间的两个数的平均数).
【解答】解:将这组数据从小到大的顺序排列为:2,2,2,4,4,7,
中位数是(2+4)÷2=3.
故选:B.
【点评】考查了确定一组数据的中位数的能力.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.注意:找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.
7.某男子排球队20名队员的身高如表:
身高(cm) 180 186 188 192 208
人数(个) 4 6 5 3 2
则此男子排球队20名队员的身高的众数和中位数分别是(单位:cm)( )
A.186,186 B.186,187 C.208,188 D.188,187
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,可得答案.
【解答】解:在这一组数据中身高为186cm的有6人,最多,故众数是186cm;
排序后处于中间位置的那个数是186cm,188cm,那么由中位数的定义可知,这组数据的中位数是187cm;
故选:B.
【点评】本题为统计题,考查众数与中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
8.一组数据:2,﹣1,0,3,﹣3,2.则这组数据的中位数和众数分别是( )
A.0,2 B.1.5,2 C.1,2 D.1,3
【分析】把这组数据按照从小到大的顺序排列,第3、4个数的平均数是中位数,在这组数据中出现次数最多的是1,得到这组数据的众数.
【解答】解:把这组数据按照从小到大的顺序排列﹣3,﹣1,0,2,2,3,
第3、4个两个数的平均数是(0+2)÷2=1,
所以中位数是1;
在这组数据中出现次数最多的是2,
即众数是2,
故选:C.
【点评】本题考查一组数据的中位数和众数,在求中位数时,首先要把这列数字按照从小到大或从的大到小排列,找出中间一个数字或中间两个数字的平均数即为所求.
9.在10,20,40,30,80,90,50,40,40,50这10个数据中,算出这组数据的极差是( )
A.40 B.70 C.80 D.90
【分析】根据极差的公式计算可得.
【解答】解:这组数据的极差是90﹣10=80.
故选:C.
【点评】极差反映了一组数据变化范围的大小,求极差的方法是用一组数据中的最大值减去最小值.
10.为了帮助本市一名患病的高中生,某班15名同学积极捐款,他们捐款数额如表:
捐款的数额(单位:元) 5 10 20 50 100
人数(单位:人) 2 4 5 3 1
关于这15名同学所捐款的数额,下列说法正确的是( )
A.众数是100 B.中位数是30 C.极差是20 D.中位数是20
【分析】根据众数、中位数、极差的定义,结合表格即可得出答案.
【解答】解:∵捐款20元的人数是5人,最多,
∴众数是20,
按照从小到大的顺序,第8人捐款是20,
所以,中位数是20,
极差为100﹣5=95.
故选:D.
【点评】本题考查了中位数、极差及众数的知识,掌握各部分的定义是关键.
二.填空题(共8小题)
11.某市2007年5月份某一周的日最高气温(单位:℃)分别为:25,28,30,29,31,32,28,这周的日最高气温的平均值是 29℃ .
【分析】利用平均数公式即可直接求解.
【解答】解:这周的日最高气温的平均值是:(25+28+30+29+31+32+28)=29℃.
故答案是:29℃.
【点评】本题考查了平均数公式,理解公式是关键.
12.超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
测试项目 创新能力 综合知识 语言表达
测试成绩(分数) 70 80 90
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是 77 分.
【分析】根据该应聘者的总成绩=创新能力×所占的比值+综合知识×所占的比值+语言表达×所占的比值即可求得.
【解答】解:根据题意,该应聘者的总成绩是:70×+80×+90×=77(分),
故答案为:77.
【点评】此题考查了加权平均数,解题的关键是熟记加权平均数的计算方法.
13.某同学用计算器求30个数据的平均数时,错将其中的一个数据105输入成15,则由此求出的平均数与实际平均数的差是 ﹣3 .
【分析】根据平均数的公式求解即可.前后数据的和相差90,则平均数相差90÷30.
【解答】解:求30个数据的平均数时,错将其中的一个数据105输入成15,即少加了90;则由此求出的平均数与实际平均数的差是﹣=﹣3.
故答案为﹣3.
【点评】本题考查的是样本平均数的求法及运用.
14.已知一组数据是3,4,7,a,中位数为4,则a= 4 .
【分析】根据中位数的定义,当数据有偶数个时,中位数即是正中间两个数的平均数,继而得出a的值.
【解答】解:∵有数据个数是偶数,且中位数是4,
∴a=4,
故答案为:4.
【点评】本题考查了中位数,熟练掌握中位数的定义是解题的关键;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.
15.某中学随机调查了15名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:一周在校的体育锻炼时间(小时) 5 6 7 8
人数 2 5 6 2
那么这15名学生这一周在校参加体育锻炼的时间的众数是 7 小时.
【分析】根据众数的概念求解.
【解答】解:这15名学生中,一周在校的体育锻炼7小时的人数最多,即众数为7.
故答案为:7.
【点评】本题考查了众数的知识,一组数据中出现次数最多的数据叫做众数.
16.数据﹣5,6,4,0,1,7,5的极差为 12 .
【分析】根据求极差的方法是用一组数据中的最大值减去最小值,找出这组数据的最大值和最小值,再求出它们的差即可.
【解答】解:极差=7﹣(﹣5)=12.
故答案为12.
【点评】此题考查了极差,用到的知识点是极差,极差反映了一组数据变化范围的大小,求极差的方法是用一组数据中的最大值减去最小值.
17.甲、乙两人在相同的情况下各打靶10次,打靶的成绩如图,这两人10次打靶平均命中环数都为7环,则S2甲 < S2乙(填“>”、“<”或“=”).
【分析】根据折线图可以得到甲、乙10次打靶的成绩,再根据方差公式s2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2]代入样本数据计算即可.
【解答】解:S2甲= [(9﹣7)2+(5﹣7)2+(7﹣7)2+(8﹣7)2+(7﹣7)2+(6﹣7)2+(8﹣7)2+(6﹣7)2+(7﹣7)2+(7﹣7)2]=1.2,
S2乙= [(2﹣7)2+(4﹣7)2+(6﹣7)2+(8﹣7)2+(7﹣7)2+(7﹣7)2+(8﹣7)2+(9﹣7)2+(9﹣7)2+(10﹣7)2]=5.4,
∵1.2<5.4,
∴S2甲<S2乙,
故答案为:<.
【点评】此题主要考查了方差,关键是掌握方差公式:s2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2].
18.一组数据:1,3,2,5,x的平均数为3,那么x= 4 ,这组数据的标准差是 .
【分析】根据已知求出x的值,再利用方差公式求出即可.
【解答】解:∵1,3,2,5,x的平均数为3,
∴=3,
x=4,
∴s2= [(1﹣3)2+(3﹣3)2+(2﹣3)2+(5﹣3)2+(4﹣3)2]
=2.
∴s=
∴这组数据的标准差是.
故答案为:4,.
【点评】此题主要考查了方差公式的应用,根据已知得出x的值,熟记方差公式是解决问题的关键.
三.解答题(共8小题)
19.下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
考试类别 平时 期中考试 期末考试
第一单元 第二单元 第三单元 第四单元
成绩 88 86 90 92 90 96
(1)李刚同学6次成绩的极差是 10分 .
(2)李刚同学6次成绩的中位数是 90分 .
(3)李刚同学平时成绩的平均数是 89分 .
(4)如果用下图的权重给李刚打分,他应该得多少分?(满分100分,写出解题过程)
【分析】(1)极差就是最大值与最小值的差,依据定义即可求解;
(2)中位数就是大小处于中间位置的数,根据定义求解;
(3)只要运用求平均数公式:即可求出,为简单题;
(4)利用加权平均数公式即可求解.
【解答】解:(1)最大值是96分,最小是86分,因而极差是96﹣86=10分,故答案是:10分;
(2)成绩从大到小排列为96,92,90,90,88,86,则中位数是:=90分,故答案是:90分;
(3)=89分,故答案是:89分;
(4)89×10%+90×30%+96×60%=93.5分.
答:李刚的总评分应该是93.5分.
【点评】本题考查的是平均数、中位数和极差,要注意,当所给数据有单位时,所求得的平均数、中位数和极差与原数据的单位相同,不要漏单位.
20.年终将至,上级管理部门对甲、乙两个银行的服务情况进行了抽查.如图反映了被抽查对象对两个银行服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为0分、1分、2分、4分.
(1)请问:甲银行的用户满意度分数的众数为 ,乙银行的用户满意度分数的中位数为 ;
(2)分别求出甲、乙两银行的用户满意度分数的平均值;
(3)请你根据所学的统计知识,判断哪个银行的用户满意度较高,并简要说明理由.
【分析】(1)找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据;
(2)根据平均数的公式就可以求解;
(3)求出两个银行的满意度,进行比较就可以.
【解答】解:(1)甲银行的用户满意度分数的众数为2;乙银行的用户满意度分数的中位数为2;
(2)甲银行抽查用户数为:500+1000+2000+1000=4500(户),
乙银行抽查用户数为:100+900+2200+1300=4500(户).
所以甲银行满意度分数的平均值=(500×0+1000×1+2000×2+1000×4)=2(分),
乙银行满意度分数的平均值=(100×0+900×1+2200×2+1300×4)=(分).
答:甲、乙两银行用户满意度分数的平均值分别为2分,分;
(3)因为乙银行用户满意度分数的平均值较高(或较满意和很满意的人数较多),
所以乙银行的用户满意度较高.
【点评】此题提高了学生的综合应用能力,解题的关键是理解平均数、众数和中位数的意义.熟悉条形图的应用.
21.为了帮助贫困失学儿童重返学校,某校发起参加“爱心储蓄”活动,鼓励学生将自己的压岁钱、零用钱存入银行,定期一年,到期后可取回本金,而把利息捐给贫困儿童.该校共有学生1200人,下列两个图为该校各年级学生人数比例分布情况图和学生人均存款情况图.
(1)该校九年级学生存款总数为 72000 元;
(2)该校学生的人均存款额为多少元?
(3)已知银行一年期定期存款的年利率为2.25%(“爱心储蓄”免征利息税),且每351元能够提供一位失学儿童一学年的基本费用.那么该校一年能够帮助多少名贫困失学儿童?
【分析】(1)由扇形统计图和条形统计图可知:该校九年级学生存款总数=九年级的人数×九年级的人均存款额;
(2)该校学生的人均存款额=;
(3)计算出该校学生存款总额,又知利息=本金×利率×期限,则计算出利息,则可以计算出帮助贫困失学儿童的人数=.
【解答】解:(1)该校九年级学生存款总数=九年级的人数×九年级的人均存款额=1200×25%×240=72000元;
(2)该校学生的人均存款额===325元;
(3)该校学生存款额=325×1200=390000元,又知利息=本金×利率×期限,则利息=390000×2.25%×1=8775元,则可以帮助贫困失学儿童的人数==25人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
22.某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生本次测试成绩的众数是a,中位数为b,求的值.
【分析】(1)根据题意可以得到关于x、y的二元一次方程组,解方程组即可求得x、y的值.
(2)众数是一组数据中出现次数最多的数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.根据定义求出a,b,再求代数式的值.
【解答】解:(1)由题意,有
解得.
(2)由(1),众数a=90,中位数b=80.
∴.
【点评】本题为综合体.考查了平均数、众数与中位数的意义,以及解二元一次和二次根式的化简.
23.国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
根据以上信息,回答下列问题:
(1)A组的人数是 50 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 C ;
(3)根据统计数据估计该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有 14000 人.
【分析】(1)根据题意和统计图可以得到A组的人数;
(2)根据(1)中补全的统计图可以得到这组数据的中位数落在哪一组;
(3)根据统计图中的数据可以估计该地区达到国家规定的每天在校体育锻炼时间的人数.
【解答】解:(1)由统计图可得,
A组人数为:60÷24%﹣60﹣120﹣20=50,
故答案为:50,补全的条形统计图如右图所示,
(2)由补全的条形统计图可得,中位数落在C组,
故答案为:C;
(3)由题意可得,
该地区25 000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有:25000×(48%+8%)=14000(人),
故答案为:14000.
【点评】本题考查中位数、用样本估计总体、扇形统计图、条形统计图,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
24.甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 空间与图形 统计与概率 综合与实践
学生甲 90 93 89 90
学生乙 94 92 94 86
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
【分析】(1)将一组数据按照从小到大(或从大到小)的顺序排列,处于中间位置的数就是这组数据的中位数进行分析;
(2)数学综合素质成绩=数与代数成绩×+空间与图形成绩×+统计与概率成绩×+综合与实践成绩×,依此分别进行计算即可求解.
【解答】解:(1)甲的成绩从小到大的顺序排列为:89,90,90,93,中位数为90;
乙的成绩从小到大的顺序排列为:86,92,94,94,中位数为(92+94)÷2=93.
答:甲成绩的中位数是90,乙成绩的中位数是93;
(2)3+3+2+2=10
甲90×+93×+89×+90×
=27+27.9+17.8+18
=90.7(分)
乙94×+92×+94×+86×
=28.2+27.6+18.8+17.2
=91.8(分)
答:甲的数学综合素质成绩为90.7分,乙的数学综合素质成绩为91.8分.
【点评】此题考查了中位数和加权平均数,用到的知识点是中位数和加权平均数,掌握它们的计算公式是本题的关键.
25.某品牌汽车的销售公司有营销人员14人,销售部为制定营销人员的月销售汽车定额,统计了这14人在某月的销售量如下表:
销售辆数 20 17 13 8 5 4
人 数 1 1 2 5 3 2
(1)这14位销售员该月销售某品牌汽车的平均数、众数和中位数各是多少辆?
(2)销售部经理把每位销售员每月销售汽车定额为9辆,你认为是否合理?为什么?如果不合理,请你设计一个比较合理的销售定额,并说明理由.
【分析】(1)用加权平均数的求法求得其平均数,出现最多的数据为众数,排序后位于中间位置的数即为中位数.
【解答】解:(1)平均数:=9;
众数:8;中位数:8
(2)不合理,因为达到指标的人数太少.应选8比较合理,因为中位数和众数都是8,能代表一般水平.
【点评】本题考查了中位数、众数的确定及加权平均数的计算方法,解决本题的关键是正确的从表中整理出所有数据,并进行正确的计算和分析.
26.在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有 21 人;
(2)补全下表中空缺的三个统计量:
平均数(分) 中位数(分) 众数(分)
一班 77.6 80 80
二班 77.6 70 90
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.
【分析】(1)根据条形统计图得到参赛人数,然后根据每个级别所占比例求出成绩在70分以上的人数;
(2)由上题中求得的总人数分别求出各个成绩段的人数,然后可以求平均数、中位数、众数;
(3)根据其成绩,作出合理的分析即可.
【解答】解:(1)一班参赛人数为:6+12+2+5=25(人),
∵两班参赛人数相同,
∴二班成绩在70分以上(包括70分)的人数为25×84%=21人;
(2)平均数:90×44%+80×4%+70×36%+60×16%=77.6(分);
中位数:70(分);
众数:80(分).
填表如下:
平均数(分) 中位数(分) 众数(分)
一班 77.6 80 80
二班 77.6 70 90
(3)①平均数相同的情况下,二班的成绩更好一些.
②请一班的同学加强基础知识训练,争取更好的成绩.
故答案为:21;80,77.6,70.
【点评】本题考查了各种统计图之间的相互转化的知识,在解决本题时关键的地方是根据题目提供的信息得到相应的解决下一题的信息,考查了学生们加工信息的能力.
一.选择题(共10小题)
1.某班抽取6名同学进行体育达标测试,成绩如下:80,90,75,80,75,80.下列关于对这组数据的描述错误的是( )
A.众数是80 B.平均数是80 C.中位数是75 D.极差是15
2.一组数据2,3,5,7,8的平均数是( )
A.2 B.3 C.4 D.5
3.甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元,若将甲种8千克,乙种10千克,丙种3千克混在一起,则售价应定为每千克( )
A.7元 B.6.8元 C.7.5元 D.8.6元
4.有8个数的平均数是11,另外有12个数的平均数是12,这20个数的平均数是( )
A.11.6 B.2.32 C.23.2 D.11.5
5.5个相异自然数的平均数为12,中位数为17,这5个自然数中最大一个的可能值的最大值是( )
A.21 B.22 C.23 D.24
6.一组数据2,2,2,4,4,7的中位数是( )
A.2 B.3 C.4 D.7
7.某男子排球队20名队员的身高如表:
身高(cm) 180 186 188 192 208
人数(个) 4 6 5 3 2
则此男子排球队20名队员的身高的众数和中位数分别是(单位:cm)( )
A.186,186 B.186,187 C.208,188 D.188,187
8.一组数据:2,﹣1,0,3,﹣3,2.则这组数据的中位数和众数分别是( )
A.0,2 B.1.5,2 C.1,2 D.1,3
9.在10,20,40,30,80,90,50,40,40,50这10个数据中,算出这组数据的极差是( )
A.40 B.70 C.80 D.90
10.为了帮助本市一名患病的高中生,某班15名同学积极捐款,他们捐款数额如表:
捐款的数额(单位:元) 5 10 20 50 100
人数(单位:人) 2 4 5 3 1
关于这15名同学所捐款的数额,下列说法正确的是( )
A.众数是100 B.中位数是30 C.极差是20 D.中位数是20
二.填空题(共8小题)
11.某市2007年5月份某一周的日最高气温(单位:℃)分别为:25,28,30,29,31,32,28,这周的日最高气温的平均值是 .
12.超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
测试项目 创新能力 综合知识 语言表达
测试成绩(分数) 70 80 90
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是 分.
13.某同学用计算器求30个数据的平均数时,错将其中的一个数据105输入成15,则由此求出的平均数与实际平均数的差是 .
14.已知一组数据是3,4,7,a,中位数为4,则a= .
15.某中学随机调查了15名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:
一周在校的体育锻炼时间(小时) 5 6 7 8
人数 2 5 6 2
那么这15名学生这一周在校参加体育锻炼的时间的众数是 小时.
16.数据﹣5,6,4,0,1,7,5的极差为 .
17.甲、乙两人在相同的情况下各打靶10次,打靶的成绩如图,这两人10次打靶平均命中环数都为7环,则S2甲 S2乙(填“>”、“<”或“=”).
18.一组数据:1,3,2,5,x的平均数为3,那么x= ,这组数据的标准差是 .
三.解答题(共8小题)
19.下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
考试类别 平时 期中考试 期末考试
第一单元 第二单元 第三单元 第四单元
成绩 88 86 90 92 90 96
(1)李刚同学6次成绩的极差是 .
(2)李刚同学6次成绩的中位数是 .
(3)李刚同学平时成绩的平均数是 .
(4)如果用下图的权重给李刚打分,他应该得多少分?(满分100分,写出解题过程)
20.年终将至,上级管理部门对甲、乙两个银行的服务情况进行了抽查.如图反映了被抽查对象对两个银行服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为0分、1分、2分、4分.
(1)请问:甲银行的用户满意度分数的众数为 ,乙银行的用户满意度分数的中位数为 ;
(2)分别求出甲、乙两银行的用户满意度分数的平均值;
(3)请你根据所学的统计知识,判断哪个银行的用户满意度较高,并简要说明理由.
21.为了帮助贫困失学儿童重返学校,某校发起参加“爱心储蓄”活动,鼓励学生将自己的压岁钱、零用钱存入银行,定期一年,到期后可取回本金,而把利息捐给贫困儿童.该校共有学生1200人,下列两个图为该校各年级学生人数比例分布情况图和学生人均存款情况图.
(1)该校九年级学生存款总数为 元;
(2)该校学生的人均存款额为多少元?
(3)已知银行一年期定期存款的年利率为2.25%(“爱心储蓄”免征利息税),且每351元能够提供一位失学儿童一学年的基本费用.那么该校一年能够帮助多少名贫困失学儿童?
22.某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生本次测试成绩的众数是a,中位数为b,求的值.
23.国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有 人.
24.甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 空间与图形 统计与概率 综合与实践
学生甲 90 93 89 90
学生乙 94 92 94 86
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
25.某品牌汽车的销售公司有营销人员14人,销售部为制定营销人员的月销售汽车定额,统计了这14人在某月的销售量如下表:
销售辆数 20 17 13 8 5 4
人 数 1 1 2 5 3 2
(1)这14位销售员该月销售某品牌汽车的平均数、众数和中位数各是多少辆?
(2)销售部经理把每位销售员每月销售汽车定额为9辆,你认为是否合理?为什么?如果不合理,请你设计一个比较合理的销售定额,并说明理由.
26.在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有 人;
(2)补全下表中空缺的三个统计量:
平均数(分) 中位数(分) 众数(分)
一班 77.6 80
二班 90
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.
2020年青岛新版上册数学八年级《第4章 数据分析》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.某班抽取6名同学进行体育达标测试,成绩如下:80,90,75,80,75,80.下列关于对这组数据的描述错误的是( )
A.众数是80 B.平均数是80 C.中位数是75 D.极差是15
【分析】根据平均数,中位数,众数及极差的概念进行判断.
【解答】解:将6名同学的成绩从小到大排列,第3、4个数都是80,故中位数是80,
∴答案C是错误的.
故选:C.
【点评】本题重点考查平均数,中位数,众数及极差的概念及其求法.
2.一组数据2,3,5,7,8的平均数是( )
A.2 B.3 C.4 D.5
【分析】根据平均数的定义计算.
【解答】解:数据2,3,5,7,8的平均数==5.
故选:D.
【点评】本题考查了平均数:平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.
3.甲、乙、丙三种糖果的售价分别为每千克6元、7元、8元,若将甲种8千克,乙种10千克,丙种3千克混在一起,则售价应定为每千克( )
A.7元 B.6.8元 C.7.5元 D.8.6元
【分析】根据加权平均数的计算方法:先求出所有糖果的总钱数,再除以糖果的总质量,即可得出答案.
【解答】解:售价应定为:≈6.8(元);
故选:B.
【点评】本题考查的是加权平均数的求法.本题易出现的错误是对加权平均数的理解不正确,而求6、7、8这三个数的平均数.
4.有8个数的平均数是11,另外有12个数的平均数是12,这20个数的平均数是( )
A.11.6 B.2.32 C.23.2 D.11.5
【分析】根据平均数的公式求解即可,8个数的和加12个数的和除以20即可.
【解答】解:根据平均数的求法:共(8+12)=20个数,这些数之和为8×11+12×12=232,故这些数的平均数是=11.6.
故选:A.
【点评】本题考查的是样本平均数的求法..
5.5个相异自然数的平均数为12,中位数为17,这5个自然数中最大一个的可能值的最大值是( )
A.21 B.22 C.23 D.24
【分析】根据5个相异自然数的平均数为12,得到5个自然数的和,又因为中位数为17,求数据中的最大数,所以可得出这组数据,即可求得这5个自然数中最大一个的值.
【解答】解:∵5个相异自然数的平均数为12
∴5个相异自然数的和为60;
∵中位数为17,
∴这5个数中有2个数比17小,有两个数比17大;
又∵求这5个数中的最大一个的可能值的最大值,
∴设这5个数中两个最小的数为0和1,而比17大的最小的自然数是18,
∴剩下的第5个数是:60﹣0﹣1﹣17﹣18=24,即第5个数是24,
∴这5个数为0,1,17,18,24.
∴这5个自然数中最大一个的可能值的最大值是24;
故选:D.
【点评】考查中位数和平均数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数,如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
6.一组数据2,2,2,4,4,7的中位数是( )
A.2 B.3 C.4 D.7
【分析】中位数是指将一组数据按大小顺序排列后,处在最中间的一个数(或处在最中间的两个数的平均数).
【解答】解:将这组数据从小到大的顺序排列为:2,2,2,4,4,7,
中位数是(2+4)÷2=3.
故选:B.
【点评】考查了确定一组数据的中位数的能力.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.注意:找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求.如果是偶数个则找中间两位数的平均数.
7.某男子排球队20名队员的身高如表:
身高(cm) 180 186 188 192 208
人数(个) 4 6 5 3 2
则此男子排球队20名队员的身高的众数和中位数分别是(单位:cm)( )
A.186,186 B.186,187 C.208,188 D.188,187
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,可得答案.
【解答】解:在这一组数据中身高为186cm的有6人,最多,故众数是186cm;
排序后处于中间位置的那个数是186cm,188cm,那么由中位数的定义可知,这组数据的中位数是187cm;
故选:B.
【点评】本题为统计题,考查众数与中位数的意义.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数),叫做这组数据的中位数.如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.
8.一组数据:2,﹣1,0,3,﹣3,2.则这组数据的中位数和众数分别是( )
A.0,2 B.1.5,2 C.1,2 D.1,3
【分析】把这组数据按照从小到大的顺序排列,第3、4个数的平均数是中位数,在这组数据中出现次数最多的是1,得到这组数据的众数.
【解答】解:把这组数据按照从小到大的顺序排列﹣3,﹣1,0,2,2,3,
第3、4个两个数的平均数是(0+2)÷2=1,
所以中位数是1;
在这组数据中出现次数最多的是2,
即众数是2,
故选:C.
【点评】本题考查一组数据的中位数和众数,在求中位数时,首先要把这列数字按照从小到大或从的大到小排列,找出中间一个数字或中间两个数字的平均数即为所求.
9.在10,20,40,30,80,90,50,40,40,50这10个数据中,算出这组数据的极差是( )
A.40 B.70 C.80 D.90
【分析】根据极差的公式计算可得.
【解答】解:这组数据的极差是90﹣10=80.
故选:C.
【点评】极差反映了一组数据变化范围的大小,求极差的方法是用一组数据中的最大值减去最小值.
10.为了帮助本市一名患病的高中生,某班15名同学积极捐款,他们捐款数额如表:
捐款的数额(单位:元) 5 10 20 50 100
人数(单位:人) 2 4 5 3 1
关于这15名同学所捐款的数额,下列说法正确的是( )
A.众数是100 B.中位数是30 C.极差是20 D.中位数是20
【分析】根据众数、中位数、极差的定义,结合表格即可得出答案.
【解答】解:∵捐款20元的人数是5人,最多,
∴众数是20,
按照从小到大的顺序,第8人捐款是20,
所以,中位数是20,
极差为100﹣5=95.
故选:D.
【点评】本题考查了中位数、极差及众数的知识,掌握各部分的定义是关键.
二.填空题(共8小题)
11.某市2007年5月份某一周的日最高气温(单位:℃)分别为:25,28,30,29,31,32,28,这周的日最高气温的平均值是 29℃ .
【分析】利用平均数公式即可直接求解.
【解答】解:这周的日最高气温的平均值是:(25+28+30+29+31+32+28)=29℃.
故答案是:29℃.
【点评】本题考查了平均数公式,理解公式是关键.
12.超市决定招聘广告策划人员一名,某应聘者三项素质测试的成绩如表:
测试项目 创新能力 综合知识 语言表达
测试成绩(分数) 70 80 90
将创新能力、综合知识和语言表达三项测试成绩按5:3:2的比例计入总成绩,则该应聘者的总成绩是 77 分.
【分析】根据该应聘者的总成绩=创新能力×所占的比值+综合知识×所占的比值+语言表达×所占的比值即可求得.
【解答】解:根据题意,该应聘者的总成绩是:70×+80×+90×=77(分),
故答案为:77.
【点评】此题考查了加权平均数,解题的关键是熟记加权平均数的计算方法.
13.某同学用计算器求30个数据的平均数时,错将其中的一个数据105输入成15,则由此求出的平均数与实际平均数的差是 ﹣3 .
【分析】根据平均数的公式求解即可.前后数据的和相差90,则平均数相差90÷30.
【解答】解:求30个数据的平均数时,错将其中的一个数据105输入成15,即少加了90;则由此求出的平均数与实际平均数的差是﹣=﹣3.
故答案为﹣3.
【点评】本题考查的是样本平均数的求法及运用.
14.已知一组数据是3,4,7,a,中位数为4,则a= 4 .
【分析】根据中位数的定义,当数据有偶数个时,中位数即是正中间两个数的平均数,继而得出a的值.
【解答】解:∵有数据个数是偶数,且中位数是4,
∴a=4,
故答案为:4.
【点评】本题考查了中位数,熟练掌握中位数的定义是解题的关键;找中位数要把数据按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数.
15.某中学随机调查了15名学生,了解他们一周在校的体育锻炼时间,结果如下表所示:一周在校的体育锻炼时间(小时) 5 6 7 8
人数 2 5 6 2
那么这15名学生这一周在校参加体育锻炼的时间的众数是 7 小时.
【分析】根据众数的概念求解.
【解答】解:这15名学生中,一周在校的体育锻炼7小时的人数最多,即众数为7.
故答案为:7.
【点评】本题考查了众数的知识,一组数据中出现次数最多的数据叫做众数.
16.数据﹣5,6,4,0,1,7,5的极差为 12 .
【分析】根据求极差的方法是用一组数据中的最大值减去最小值,找出这组数据的最大值和最小值,再求出它们的差即可.
【解答】解:极差=7﹣(﹣5)=12.
故答案为12.
【点评】此题考查了极差,用到的知识点是极差,极差反映了一组数据变化范围的大小,求极差的方法是用一组数据中的最大值减去最小值.
17.甲、乙两人在相同的情况下各打靶10次,打靶的成绩如图,这两人10次打靶平均命中环数都为7环,则S2甲 < S2乙(填“>”、“<”或“=”).
【分析】根据折线图可以得到甲、乙10次打靶的成绩,再根据方差公式s2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2]代入样本数据计算即可.
【解答】解:S2甲= [(9﹣7)2+(5﹣7)2+(7﹣7)2+(8﹣7)2+(7﹣7)2+(6﹣7)2+(8﹣7)2+(6﹣7)2+(7﹣7)2+(7﹣7)2]=1.2,
S2乙= [(2﹣7)2+(4﹣7)2+(6﹣7)2+(8﹣7)2+(7﹣7)2+(7﹣7)2+(8﹣7)2+(9﹣7)2+(9﹣7)2+(10﹣7)2]=5.4,
∵1.2<5.4,
∴S2甲<S2乙,
故答案为:<.
【点评】此题主要考查了方差,关键是掌握方差公式:s2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2].
18.一组数据:1,3,2,5,x的平均数为3,那么x= 4 ,这组数据的标准差是 .
【分析】根据已知求出x的值,再利用方差公式求出即可.
【解答】解:∵1,3,2,5,x的平均数为3,
∴=3,
x=4,
∴s2= [(1﹣3)2+(3﹣3)2+(2﹣3)2+(5﹣3)2+(4﹣3)2]
=2.
∴s=
∴这组数据的标准差是.
故答案为:4,.
【点评】此题主要考查了方差公式的应用,根据已知得出x的值,熟记方差公式是解决问题的关键.
三.解答题(共8小题)
19.下面的表格是李刚同学一学期数学成绩的记录,根据表格提供的信息回答下面的问题
考试类别 平时 期中考试 期末考试
第一单元 第二单元 第三单元 第四单元
成绩 88 86 90 92 90 96
(1)李刚同学6次成绩的极差是 10分 .
(2)李刚同学6次成绩的中位数是 90分 .
(3)李刚同学平时成绩的平均数是 89分 .
(4)如果用下图的权重给李刚打分,他应该得多少分?(满分100分,写出解题过程)
【分析】(1)极差就是最大值与最小值的差,依据定义即可求解;
(2)中位数就是大小处于中间位置的数,根据定义求解;
(3)只要运用求平均数公式:即可求出,为简单题;
(4)利用加权平均数公式即可求解.
【解答】解:(1)最大值是96分,最小是86分,因而极差是96﹣86=10分,故答案是:10分;
(2)成绩从大到小排列为96,92,90,90,88,86,则中位数是:=90分,故答案是:90分;
(3)=89分,故答案是:89分;
(4)89×10%+90×30%+96×60%=93.5分.
答:李刚的总评分应该是93.5分.
【点评】本题考查的是平均数、中位数和极差,要注意,当所给数据有单位时,所求得的平均数、中位数和极差与原数据的单位相同,不要漏单位.
20.年终将至,上级管理部门对甲、乙两个银行的服务情况进行了抽查.如图反映了被抽查对象对两个银行服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为0分、1分、2分、4分.
(1)请问:甲银行的用户满意度分数的众数为 ,乙银行的用户满意度分数的中位数为 ;
(2)分别求出甲、乙两银行的用户满意度分数的平均值;
(3)请你根据所学的统计知识,判断哪个银行的用户满意度较高,并简要说明理由.
【分析】(1)找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据;
(2)根据平均数的公式就可以求解;
(3)求出两个银行的满意度,进行比较就可以.
【解答】解:(1)甲银行的用户满意度分数的众数为2;乙银行的用户满意度分数的中位数为2;
(2)甲银行抽查用户数为:500+1000+2000+1000=4500(户),
乙银行抽查用户数为:100+900+2200+1300=4500(户).
所以甲银行满意度分数的平均值=(500×0+1000×1+2000×2+1000×4)=2(分),
乙银行满意度分数的平均值=(100×0+900×1+2200×2+1300×4)=(分).
答:甲、乙两银行用户满意度分数的平均值分别为2分,分;
(3)因为乙银行用户满意度分数的平均值较高(或较满意和很满意的人数较多),
所以乙银行的用户满意度较高.
【点评】此题提高了学生的综合应用能力,解题的关键是理解平均数、众数和中位数的意义.熟悉条形图的应用.
21.为了帮助贫困失学儿童重返学校,某校发起参加“爱心储蓄”活动,鼓励学生将自己的压岁钱、零用钱存入银行,定期一年,到期后可取回本金,而把利息捐给贫困儿童.该校共有学生1200人,下列两个图为该校各年级学生人数比例分布情况图和学生人均存款情况图.
(1)该校九年级学生存款总数为 72000 元;
(2)该校学生的人均存款额为多少元?
(3)已知银行一年期定期存款的年利率为2.25%(“爱心储蓄”免征利息税),且每351元能够提供一位失学儿童一学年的基本费用.那么该校一年能够帮助多少名贫困失学儿童?
【分析】(1)由扇形统计图和条形统计图可知:该校九年级学生存款总数=九年级的人数×九年级的人均存款额;
(2)该校学生的人均存款额=;
(3)计算出该校学生存款总额,又知利息=本金×利率×期限,则计算出利息,则可以计算出帮助贫困失学儿童的人数=.
【解答】解:(1)该校九年级学生存款总数=九年级的人数×九年级的人均存款额=1200×25%×240=72000元;
(2)该校学生的人均存款额===325元;
(3)该校学生存款额=325×1200=390000元,又知利息=本金×利率×期限,则利息=390000×2.25%×1=8775元,则可以帮助贫困失学儿童的人数==25人.
【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
22.某校八年级一班20名女生某次体育测试的成绩统计如下:
成绩(分) 60 70 80 90 100
人数(人) 1 5 x y 2
(1)如果这20名女生体育成绩的平均分数是82分,求x、y的值;
(2)在(1)的条件下,设20名学生本次测试成绩的众数是a,中位数为b,求的值.
【分析】(1)根据题意可以得到关于x、y的二元一次方程组,解方程组即可求得x、y的值.
(2)众数是一组数据中出现次数最多的数;中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.根据定义求出a,b,再求代数式的值.
【解答】解:(1)由题意,有
解得.
(2)由(1),众数a=90,中位数b=80.
∴.
【点评】本题为综合体.考查了平均数、众数与中位数的意义,以及解二元一次和二次根式的化简.
23.国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
根据以上信息,回答下列问题:
(1)A组的人数是 50 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 C ;
(3)根据统计数据估计该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有 14000 人.
【分析】(1)根据题意和统计图可以得到A组的人数;
(2)根据(1)中补全的统计图可以得到这组数据的中位数落在哪一组;
(3)根据统计图中的数据可以估计该地区达到国家规定的每天在校体育锻炼时间的人数.
【解答】解:(1)由统计图可得,
A组人数为:60÷24%﹣60﹣120﹣20=50,
故答案为:50,补全的条形统计图如右图所示,
(2)由补全的条形统计图可得,中位数落在C组,
故答案为:C;
(3)由题意可得,
该地区25 000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有:25000×(48%+8%)=14000(人),
故答案为:14000.
【点评】本题考查中位数、用样本估计总体、扇形统计图、条形统计图,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
24.甲、乙两位同学参加数学综合素质测试,各项成绩如下(单位:分)
数与代数 空间与图形 统计与概率 综合与实践
学生甲 90 93 89 90
学生乙 94 92 94 86
(1)分别计算甲、乙成绩的中位数;
(2)如果数与代数、空间与图形、统计与概率、综合与实践的成绩按3:3:2:2计算,那么甲、乙的数学综合素质成绩分别为多少分?
【分析】(1)将一组数据按照从小到大(或从大到小)的顺序排列,处于中间位置的数就是这组数据的中位数进行分析;
(2)数学综合素质成绩=数与代数成绩×+空间与图形成绩×+统计与概率成绩×+综合与实践成绩×,依此分别进行计算即可求解.
【解答】解:(1)甲的成绩从小到大的顺序排列为:89,90,90,93,中位数为90;
乙的成绩从小到大的顺序排列为:86,92,94,94,中位数为(92+94)÷2=93.
答:甲成绩的中位数是90,乙成绩的中位数是93;
(2)3+3+2+2=10
甲90×+93×+89×+90×
=27+27.9+17.8+18
=90.7(分)
乙94×+92×+94×+86×
=28.2+27.6+18.8+17.2
=91.8(分)
答:甲的数学综合素质成绩为90.7分,乙的数学综合素质成绩为91.8分.
【点评】此题考查了中位数和加权平均数,用到的知识点是中位数和加权平均数,掌握它们的计算公式是本题的关键.
25.某品牌汽车的销售公司有营销人员14人,销售部为制定营销人员的月销售汽车定额,统计了这14人在某月的销售量如下表:
销售辆数 20 17 13 8 5 4
人 数 1 1 2 5 3 2
(1)这14位销售员该月销售某品牌汽车的平均数、众数和中位数各是多少辆?
(2)销售部经理把每位销售员每月销售汽车定额为9辆,你认为是否合理?为什么?如果不合理,请你设计一个比较合理的销售定额,并说明理由.
【分析】(1)用加权平均数的求法求得其平均数,出现最多的数据为众数,排序后位于中间位置的数即为中位数.
【解答】解:(1)平均数:=9;
众数:8;中位数:8
(2)不合理,因为达到指标的人数太少.应选8比较合理,因为中位数和众数都是8,能代表一般水平.
【点评】本题考查了中位数、众数的确定及加权平均数的计算方法,解决本题的关键是正确的从表中整理出所有数据,并进行正确的计算和分析.
26.在学校组织的科学素养竞赛中,每班参加比赛的人数相同,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为90分,80分,70分,60分,学校将八年级一班和二班的成绩整理并绘制成如下的统计图:
请你根据以上提供的信息解答下列问题:
(1)此次竞赛中二班成绩在70分及其以上的人数有 21 人;
(2)补全下表中空缺的三个统计量:
平均数(分) 中位数(分) 众数(分)
一班 77.6 80 80
二班 77.6 70 90
(3)请根据上述图表对这次竞赛成绩进行分析,写出两个结论.
【分析】(1)根据条形统计图得到参赛人数,然后根据每个级别所占比例求出成绩在70分以上的人数;
(2)由上题中求得的总人数分别求出各个成绩段的人数,然后可以求平均数、中位数、众数;
(3)根据其成绩,作出合理的分析即可.
【解答】解:(1)一班参赛人数为:6+12+2+5=25(人),
∵两班参赛人数相同,
∴二班成绩在70分以上(包括70分)的人数为25×84%=21人;
(2)平均数:90×44%+80×4%+70×36%+60×16%=77.6(分);
中位数:70(分);
众数:80(分).
填表如下:
平均数(分) 中位数(分) 众数(分)
一班 77.6 80 80
二班 77.6 70 90
(3)①平均数相同的情况下,二班的成绩更好一些.
②请一班的同学加强基础知识训练,争取更好的成绩.
故答案为:21;80,77.6,70.
【点评】本题考查了各种统计图之间的相互转化的知识,在解决本题时关键的地方是根据题目提供的信息得到相应的解决下一题的信息,考查了学生们加工信息的能力.
同课章节目录
- 第1章 全等三角形
- 1.1 全等三角形
- 1.2 怎样判定三角形全等
- 1.3 尺规作图
- 第2章 图形的轴对称
- 2.1 图形的轴对称
- 2.2 轴对称的基本性质
- 2.3 轴对称图形
- 2.4 线段的垂直平分线
- 2.5 角平分线的性质
- 2.6 等腰三角形
- 第3章 分式
- 3.1 分式的基本性质
- 3.2 分式的约分
- 3.3 分式的乘法与除法
- 3.4 分式的通分
- 3.5 分式的加法与减法
- 3.6 比和比例
- 3.7 可化为一元一次方程的分式方程
- 第4章 数据分析
- 4.1 加权平均数
- 4.2 中位数
- 4.3 众数
- 4.4 数据的离散程度
- 4.5 方差
- 4.6 用计算器计算平均数和方差
- 第5章 几何证明初步
- 5.1 定义与命题
- 5.2 为什么要证明
- 5.3 什么是几何证明
- 5.4 平行线的性质定理和判定定理
- 5.5 三角形内角和定理
- 5.6 几何证明举例
