2019-2020学年青岛新版上册数学七年级《第1章 基本的几何图形》单元测试卷(解析版)
文档属性
| 名称 | 2019-2020学年青岛新版上册数学七年级《第1章 基本的几何图形》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 484.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 13:31:01 | ||
图片预览

文档简介
2020年青岛新版上册数学七年级《第1章 基本的几何图形》单元测试卷
一.选择题(共10小题)
1.如图是一个生日蛋糕盒,这个盒子有几条棱( )
A.6条 B.12条 C.18条 D.24条
2.将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
A. B. C. D.
3.某同学用牙膏纸盒制作一个如图所示的笔筒,笔筒的筒底为长4.5厘米,宽3.4厘米的矩形.则该笔筒最多能放半径为0.4厘米的圆柱形铅笔( )
A.20支 B.21支 C.22支 D.25支
4.如图是由下面五种基本图形中的两种拼接而成,这两种基本图形是( )
A.①⑤ B.②④ C.③⑤ D.②⑤
5.下列图形可以作为一个正方体的展开图的是( )
A. B.
C. D.
6.下列各图经过折叠不能围成一个正方体的是( )
A. B.
C. D.
7.如图是一个正方体的展开图,则“数”字的对面的字是( )
A.核 B.心 C.素 D.养
8.如图,是一个正方体,用一个平面去截这个正方体,截面形状不可能为下图中的( )
A. B.
C. D.
9.过平面上A、B、C三点中的任意两点作直线,可作( )
A.1条 B.3条 C.1条或3条 D.无数条
10.在开会前,工作人员进行会场布置,如图为工作人员在主席台上由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是( )
A.两点之间线段最短
B.两点确定一条直线
C.垂线段最短
D.过一点可以作无数条直线
二.填空题(共8小题)
11.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有 条.
12.把一块三角板以一条直角边为轴旋转成的几何体是 .
13.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
14.图中按左侧三个图形阴影部分的特点,将右侧的图形补充完整.
15.如图是某几何体的表面展开图,则这个几何体是 .
16.如图,有三张硬纸片,用它们围成一个立体图形叫 .
17.如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对应的面上的汉字是 .
18.用一个平面截下列几何体:①长方体,②六棱柱,③球,④圆柱,⑤圆锥,截面能得到三角形的是 (填写序号即可)
三.解答题(共8小题)
19.如图,上面是一些具体的物体,下面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).
20.已知长方形的长为4cm.宽为3cm,将其绕它的一边所在的直线旋转一周,得到一个几何体,
(1)求此几何体的体积;
(2)求此几何体的表面积.(结果保留π)
21.六盒磁带按“规则方式”打包,所谓“规则方式”是指每相邻两盒必须以完全一样的面对接,最后得到的包装形状是一个长方形.已知磁带盒的大小为abc=11×7×2(单位cm).
(1)请画出示意图,给出一种打包方式,使其表面积最小;
(2)若不给出a、b、c的具体尺寸,只假定a≥b≥c,3问能否按照已知的方式打包,使其表面积最小?并说明理由.
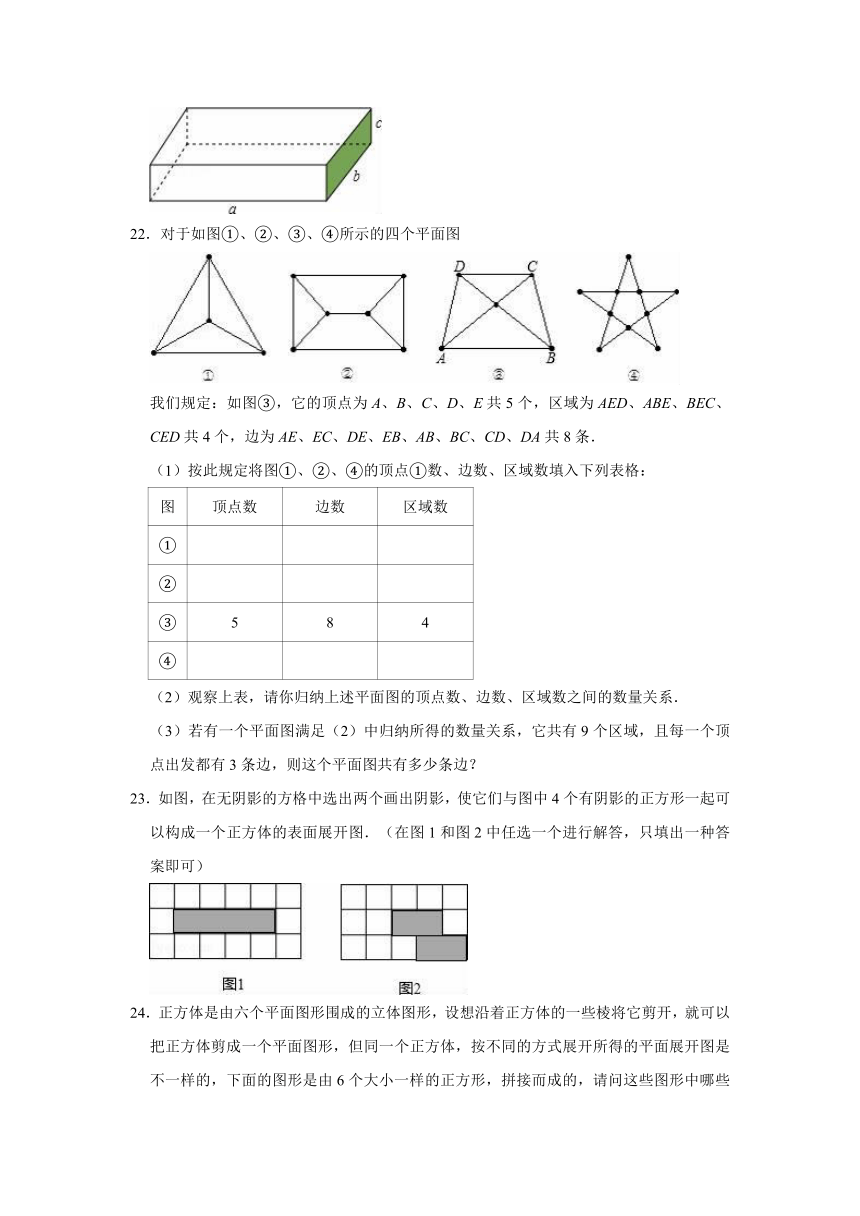
22.对于如图①、②、③、④所示的四个平面图
我们规定:如图③,它的顶点为A、B、C、D、E共5个,区域为AED、ABE、BEC、CED共4个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条.
(1)按此规定将图①、②、④的顶点①数、边数、区域数填入下列表格:
图 顶点数 边数 区域数
①
②
③ 5 8 4
④
(2)观察上表,请你归纳上述平面图的顶点数、边数、区域数之间的数量关系.
(3)若有一个平面图满足(2)中归纳所得的数量关系,它共有9个区域,且每一个顶点出发都有3条边,则这个平面图共有多少条边?
23.如图,在无阴影的方格中选出两个画出阴影,使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图.(在图1和图2中任选一个进行解答,只填出一种答案即可)
24.正方体是由六个平面图形围成的立体图形,设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形,但同一个正方体,按不同的方式展开所得的平面展开图是不一样的,下面的图形是由6个大小一样的正方形,拼接而成的,请问这些图形中哪些可以折成正方体?试试看.
25.如图是一个正方体盒子的展开图,要把﹣8、10、﹣12、8、﹣10、12些数字分别填入六个小正方形,使得按虚线折成的正方体相对面上的两个数相加得0.
26.用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.
如A(1、5、6);则B( );C( );D( );E( ).
2020年青岛新版上册数学七年级《第1章 基本的几何图形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.如图是一个生日蛋糕盒,这个盒子有几条棱( )
A.6条 B.12条 C.18条 D.24条
【分析】根据棱的定义依次数出上下面和侧面的棱数相加即可.
【解答】解:观察图形可知上下面的棱数都是6,侧面的棱数是6.
则这个盒子的棱数为:6+6+6=18.
故选:C.
【点评】本题考查了棱的定义:不同方向的两个平面相连接的部分.
2.将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
A. B. C. D.
【分析】面动成体.由题目中的图示可知:此圆台是直角梯形转成圆台的条件是:绕垂直于底的腰旋转.
【解答】解:A、是两个圆台,故A错误;
B、上面小下面大,侧面是曲面,故B正确;
C、是一个圆台,故C错误;
D、下面小上面大侧面是曲面,故D错误;
故选:B.
【点评】本题考查直角梯形转成圆台的条件:应绕垂直于底的腰旋转.
3.某同学用牙膏纸盒制作一个如图所示的笔筒,笔筒的筒底为长4.5厘米,宽3.4厘米的矩形.则该笔筒最多能放半径为0.4厘米的圆柱形铅笔( )
A.20支 B.21支 C.22支 D.25支
【分析】此题不能用面积去除面积,而应该用底面长除以直径,再用宽除以直径,用两个商相乘,得出结果.
【解答】解:若按如图方法摆放,
则△ABC为等腰三角形,其高为AD,
则AB=0.8=,BD=0.4+=,
由勾股定理,得AD=≈0.65276,
∵0.8+4×0.65276=3.411>3.4,这种情况不可能,
这样有4个高<2.8+0.4+0.4<3.6,最后还剩下0.9×3.4还可以放4支.
这样,长放0.4+(4个<0.7)+0.4+0.8<4.4<4.5,
宽放4个0.8=3.2<3.4,共4+3+4+3+4+4=22支(如图).
故选:C.
【点评】此处应注意不足0.8厘米放不下一支.
4.如图是由下面五种基本图形中的两种拼接而成,这两种基本图形是( )
A.①⑤ B.②④ C.③⑤ D.②⑤
【分析】根据分割与组合的原理对图形进行分析即解.
【解答】解:分析原图可得:原图由②⑤两种图案组成.
故选:D.
【点评】此题考查了平面图形的分割与组成,主要培养学生的观察能力和空间想象能力.
5.下列图形可以作为一个正方体的展开图的是( )
A. B.
C. D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:A、不能作为一个正方体的展开图,故本选项错误;
B、不能作为一个正方体的展开图,故本选项错误;
C、能作为一个正方体的展开图,故本选项正确;
D、不能作为一个正方体的展开图,故本选项错误;
故选:C.
【点评】本题考查了几何体的展开图,属于基础题,注意培养自己的空间想象能力.
6.下列各图经过折叠不能围成一个正方体的是( )
A. B.
C. D.
【分析】由平面图形的折叠及正方体的表面展开图的特点解题.只要有“田”“凹”“一线超过四个正方形”字格的展开图都不是正方体的表面展开图.
【解答】解:A、是正方体的展开图,不符合题意;
B、是正方体的展开图,不符合题意;
C、是正方体的展开图,不符合题意;
D、不是正方体的展开图,缺少一个底面,符合题意.
故选:D.
【点评】本题考查了正方体的展开图,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.
7.如图是一个正方体的展开图,则“数”字的对面的字是( )
A.核 B.心 C.素 D.养
【分析】利用正方体及其表面展开图的特点求解即可.
【解答】解:这是一个正方体的平面展开图,共有六个面,其中“数”字的对面的字是养.
故选:D.
【点评】本题考查了正方体相对两个面上文字的知识,解答本题的关键是从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念.
8.如图,是一个正方体,用一个平面去截这个正方体,截面形状不可能为下图中的( )
A. B.
C. D.
【分析】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此截面的形状可能是:三角形、四边形、五边形、六边形.
【解答】解:用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,不可能为七边形.
故选:D.
【点评】本题考查正方体的截面.正方体的截面的四种情况应熟记.
9.过平面上A、B、C三点中的任意两点作直线,可作( )
A.1条 B.3条 C.1条或3条 D.无数条
【分析】分三点共线和不共线两种情况作出图形,即可得解.
【解答】解:如图,过平面上A、B、C三点中的任意两点作直线,可作1条或3条.
故选C.
【点评】本题考查了直线、射线、线段,要注意分情况讨论,作出图形更形象直观.
10.在开会前,工作人员进行会场布置,如图为工作人员在主席台上由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是( )
A.两点之间线段最短
B.两点确定一条直线
C.垂线段最短
D.过一点可以作无数条直线
【分析】根据直线的性质:两点确定一条直线可得答案.
【解答】解:由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是两点确定一条直线,
故选:B.
【点评】此题主要考查了直线的性质,关键是掌握两点确定一条直线.
二.填空题(共8小题)
11.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有 4 条.
【分析】在长方体,棱与面之间的关系有平行和垂直两种.
【解答】解:与平面ADHE垂直的棱有:AB,DC,HG,EF.共4条.
故答案为4.
【点评】本题考查的知识点为:与一个平面内的一条直线垂直的直线就与这个平面垂直.
12.把一块三角板以一条直角边为轴旋转成的几何体是 圆锥 .
【分析】本题是一块三角板围绕一条直角边为对称轴旋转一周,根据面动成体的原理即可解.
【解答】解:一块三角板以一条直角边为轴旋转成的几何体是圆锥.
【点评】此题考查了立体图形和平面图形的理解能力,主要培养学生的观察能力和空间想象能力.
13.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 24 .
【分析】根据几何体表面积的计算公式,从正方体毛坯一角挖去一个小正方体得到的零件的表面积等于原正方体表面积,即可得出答案.
【解答】解:挖去一个棱长为1的小正方体,得到的图形与原图形表面积相等,
则表面积是2×2×6=24.
故答案为:24.
【点评】此题考查了几何体的表面积,本题有多种解法,一种是把每个面的面积计算出来然后相加,这样比较麻烦,另一种算法就是解答中的这种,这种方法的关键是能想象出得到的图形与原图形表面积相等.
14.图中按左侧三个图形阴影部分的特点,将右侧的图形补充完整.
【分析】根据图形中阴影的运动规律即可解,阴影部分是逆时针转动的.
【解答】解:观察图形可知,阴影部分是逆时针转动的,所以右侧的图形是.
故答案为.
【点评】仔细观察图形,找出旋转的规律,是解题的关键.
15.如图是某几何体的表面展开图,则这个几何体是 圆柱体 .
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:一个长方形和两个圆折叠后,能围成的几何体是圆柱.
故答案为:圆柱体.
【点评】本题考查了由三视图判断几何体的知识,熟记常见几何体的平面展开图的特征,是解决此类问题的关键.
16.如图,有三张硬纸片,用它们围成一个立体图形叫 圆柱体 .
【分析】利用已知图形结合三视图的有关知识,可以判断出它所组成的图形.
【解答】解:利用三视图有关知识,矩形只能组成圆柱形,两个圆正好组成圆柱的上底与下底.
故填:圆柱体
【点评】此题主要考查了三视图有关知识,以及考查同学们的立体思维.
17.如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对应的面上的汉字是 学 .
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“生”与“学”是相对面.
故答案为:学.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
18.用一个平面截下列几何体:①长方体,②六棱柱,③球,④圆柱,⑤圆锥,截面能得到三角形的是 ①②⑤ (填写序号即可)
【分析】根据用一个平面截一个几何体得到的面叫做几何体的截面,利用常见图形分析得出即可.
【解答】解:①长方体能截出三角形;
②六棱柱沿对角线截几何体可以截出三角形;
③球不能截出三角形;
④圆柱不能截出三角形;
⑤圆锥能截出三角形;
故截面可能是三角形的有①②⑤共3个.
故答案为:①②⑤.
【点评】本题考查几何体的截面,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.
三.解答题(共8小题)
19.如图,上面是一些具体的物体,下面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).
【分析】结合给出事物的特征,抽象出所对应的立体图形,关键是运用空间想象能力.
【解答】解:埃及金字塔﹣﹣(2)
西瓜﹣﹣(3)
水杯﹣﹣(1)
房屋﹣﹣(5).
【点评】本题要掌握常见立体图形的特征,注意培养观察力和空间想象能力.
20.已知长方形的长为4cm.宽为3cm,将其绕它的一边所在的直线旋转一周,得到一个几何体,
(1)求此几何体的体积;
(2)求此几何体的表面积.(结果保留π)
【分析】(1)旋转后的几何体是圆柱体,先确定出圆柱的底面半径和高,再根据圆柱的体积公式计算即可求解;
(2)根据圆柱的表面积公式计算即可求解.
【解答】解:长方形绕一边旋转一周,得圆柱.
(1)情况①:π×32×4=36π(cm3);
情况②:π×42×3=48π(cm3);
(2)情况①:
π×3×2×4+π×32×2
=24π+18π
=42π(cm2);
情况②:
π×4×2×3+π×42×2
=24π+32π
=56π(cm2).
【点评】本题主要考查的是点、线、面、体,根据图形确定出圆柱的底面半径和高的长是解题的关键.
21.六盒磁带按“规则方式”打包,所谓“规则方式”是指每相邻两盒必须以完全一样的面对接,最后得到的包装形状是一个长方形.已知磁带盒的大小为abc=11×7×2(单位cm).
(1)请画出示意图,给出一种打包方式,使其表面积最小;
(2)若不给出a、b、c的具体尺寸,只假定a≥b≥c,3问能否按照已知的方式打包,使其表面积最小?并说明理由.
【分析】一盒火柴的图形如图甲所示,则三个面的面积记为A=bc,B=ac,C=ab;考虑到6盒火柴,6=1×6=2×3,因此,规则方式打包有两类:“1×6”和“2×3”.(1)已知磁带盒的大小为abc=11×7×2,分别求出两种方式的表面积,比较大小即可;(2)已知a≥b≥c,可设a=46mm,b=36mm,c=16mm,分别求出两种方式的表面积,比较大小即可.
【解答】解:(1)设:三个面的面积记为A=bc,B=ac,C=ab,
①在1×6的方式下,打包方式如图乙,这时,表面积
S乙=2C+12B+12A=2×11×7+12×11×2+12×7×2=586(cm2);
②在2×3的方式下,打包方式如图丙,这时,表面积
S丙=4C+6B+12A=4×11×7+6×11×2+12×7×2=608(cm2);
因为S乙<S丙,所以最小表面积的打包方式是1×6.
(2)若a≥b≥c,则单叠(即1*6方式)打包的最小表面积S=2ab+12ac+12bc;
双叠(即2*3方式)打包最小表面积S'=4ab+6ac+12bc.所以S﹣S'=2a(3c﹣b).
所以:当a≥b,且c≤b<3c时,最小表面积为双叠
当a≥b>3c时,最小表面积为单叠
当a≥b=3c时,两种方式一样大
【点评】此题考查了平面图形的有关知识,培养学生的观察能力和图形的组合能力;注意其中的一个面被上面的立方体覆盖.
22.对于如图①、②、③、④所示的四个平面图
我们规定:如图③,它的顶点为A、B、C、D、E共5个,区域为AED、ABE、BEC、CED共4个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条.
(1)按此规定将图①、②、④的顶点①数、边数、区域数填入下列表格:
图 顶点数 边数 区域数
①
②
③ 5 8 4
④
(2)观察上表,请你归纳上述平面图的顶点数、边数、区域数之间的数量关系.
(3)若有一个平面图满足(2)中归纳所得的数量关系,它共有9个区域,且每一个顶点出发都有3条边,则这个平面图共有多少条边?
【分析】(1)根据规定结合图形即可填充表格.
(2)根据所填的表格即可得出平面图的顶点数、边数、区域数之间的数量关系.
(3)根据(2)的关系直接写出答案.
【解答】解:(1)按此规定将图①、②、④的顶点数、边数、区域数填入下列表格:
图 顶点数 边数 区域数
① 4 6 3
② 6 9 4
③ 5 8 4
④ 10 15 6
(2)由表格得:顶点数+区域数=边数+1,
(3)设顶点数为x,根据题意可知,x+9=+1,
得出x=16
每个顶点发出三个3边,有9个区域数,
则有16个顶点,24条边.
【点评】本题考查平面图形的知识,有一定难度,关键是理解题意,根据特殊推出一般规律.
23.如图,在无阴影的方格中选出两个画出阴影,使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图.(在图1和图2中任选一个进行解答,只填出一种答案即可)
【分析】和一个正方体的平面展开图相比较,可得出一个正方体11种平面展开图.
【解答】解:只写出一种答案即可.(4分)
图1:
图2:
【点评】正方体共有11种表面展开图,把11种展开图都去掉一个面得无盖的正方体展开图,把相同的归为一种得无盖正方体有8种表面展开图.
24.正方体是由六个平面图形围成的立体图形,设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形,但同一个正方体,按不同的方式展开所得的平面展开图是不一样的,下面的图形是由6个大小一样的正方形,拼接而成的,请问这些图形中哪些可以折成正方体?试试看.
【分析】由平面图形的折叠及正方体的展开图解题.
【解答】解:由图示可知:图1,图2,图3,图4,图6,图10,图11,图12均可以折成正方体.
【点评】解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意有田字的不能展开成正方体.
25.如图是一个正方体盒子的展开图,要把﹣8、10、﹣12、8、﹣10、12些数字分别填入六个小正方形,使得按虚线折成的正方体相对面上的两个数相加得0.
【分析】先根据正方体及其表面展开图的特点,找到相对的面,再相加得0的两个数填入即可.
【解答】解:﹣8和8,﹣12和12,﹣10和10互为相反数,
所作图形如下:
.
【点评】本题考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
26.用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.
如A(1、5、6);则B( 1,3,4 );C( 1,2,3,4 );D( 5 );E( 3,5,6 ).
【分析】分别分析其余四种图形的所有的截面情况,再写出答案.
【解答】解:B三棱锥,截面有可能是三角形,正方形,梯形
C正方体,截面有可能是三角形,四边形(矩形,正方形,梯形),五边形,六边形
D球体,截面只可能是圆
E圆柱体,截面有可能是椭圆,圆,矩形,
因此应该写B(1、3、4);C(1、2、3、4);D(5);E(3、5、6).
【点评】截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,亲自动手做一做,从中学会分析和归纳的思想方法.
一.选择题(共10小题)
1.如图是一个生日蛋糕盒,这个盒子有几条棱( )
A.6条 B.12条 C.18条 D.24条
2.将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
A. B. C. D.
3.某同学用牙膏纸盒制作一个如图所示的笔筒,笔筒的筒底为长4.5厘米,宽3.4厘米的矩形.则该笔筒最多能放半径为0.4厘米的圆柱形铅笔( )
A.20支 B.21支 C.22支 D.25支
4.如图是由下面五种基本图形中的两种拼接而成,这两种基本图形是( )
A.①⑤ B.②④ C.③⑤ D.②⑤
5.下列图形可以作为一个正方体的展开图的是( )
A. B.
C. D.
6.下列各图经过折叠不能围成一个正方体的是( )
A. B.
C. D.
7.如图是一个正方体的展开图,则“数”字的对面的字是( )
A.核 B.心 C.素 D.养
8.如图,是一个正方体,用一个平面去截这个正方体,截面形状不可能为下图中的( )
A. B.
C. D.
9.过平面上A、B、C三点中的任意两点作直线,可作( )
A.1条 B.3条 C.1条或3条 D.无数条
10.在开会前,工作人员进行会场布置,如图为工作人员在主席台上由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是( )
A.两点之间线段最短
B.两点确定一条直线
C.垂线段最短
D.过一点可以作无数条直线
二.填空题(共8小题)
11.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有 条.
12.把一块三角板以一条直角边为轴旋转成的几何体是 .
13.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 .
14.图中按左侧三个图形阴影部分的特点,将右侧的图形补充完整.
15.如图是某几何体的表面展开图,则这个几何体是 .
16.如图,有三张硬纸片,用它们围成一个立体图形叫 .
17.如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对应的面上的汉字是 .
18.用一个平面截下列几何体:①长方体,②六棱柱,③球,④圆柱,⑤圆锥,截面能得到三角形的是 (填写序号即可)
三.解答题(共8小题)
19.如图,上面是一些具体的物体,下面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).
20.已知长方形的长为4cm.宽为3cm,将其绕它的一边所在的直线旋转一周,得到一个几何体,
(1)求此几何体的体积;
(2)求此几何体的表面积.(结果保留π)
21.六盒磁带按“规则方式”打包,所谓“规则方式”是指每相邻两盒必须以完全一样的面对接,最后得到的包装形状是一个长方形.已知磁带盒的大小为abc=11×7×2(单位cm).
(1)请画出示意图,给出一种打包方式,使其表面积最小;
(2)若不给出a、b、c的具体尺寸,只假定a≥b≥c,3问能否按照已知的方式打包,使其表面积最小?并说明理由.
22.对于如图①、②、③、④所示的四个平面图
我们规定:如图③,它的顶点为A、B、C、D、E共5个,区域为AED、ABE、BEC、CED共4个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条.
(1)按此规定将图①、②、④的顶点①数、边数、区域数填入下列表格:
图 顶点数 边数 区域数
①
②
③ 5 8 4
④
(2)观察上表,请你归纳上述平面图的顶点数、边数、区域数之间的数量关系.
(3)若有一个平面图满足(2)中归纳所得的数量关系,它共有9个区域,且每一个顶点出发都有3条边,则这个平面图共有多少条边?
23.如图,在无阴影的方格中选出两个画出阴影,使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图.(在图1和图2中任选一个进行解答,只填出一种答案即可)
24.正方体是由六个平面图形围成的立体图形,设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形,但同一个正方体,按不同的方式展开所得的平面展开图是不一样的,下面的图形是由6个大小一样的正方形,拼接而成的,请问这些图形中哪些可以折成正方体?试试看.
25.如图是一个正方体盒子的展开图,要把﹣8、10、﹣12、8、﹣10、12些数字分别填入六个小正方形,使得按虚线折成的正方体相对面上的两个数相加得0.
26.用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.
如A(1、5、6);则B( );C( );D( );E( ).
2020年青岛新版上册数学七年级《第1章 基本的几何图形》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.如图是一个生日蛋糕盒,这个盒子有几条棱( )
A.6条 B.12条 C.18条 D.24条
【分析】根据棱的定义依次数出上下面和侧面的棱数相加即可.
【解答】解:观察图形可知上下面的棱数都是6,侧面的棱数是6.
则这个盒子的棱数为:6+6+6=18.
故选:C.
【点评】本题考查了棱的定义:不同方向的两个平面相连接的部分.
2.将下列平面图形绕轴旋转一周,可得到图中所示的立体图形的是( )
A. B. C. D.
【分析】面动成体.由题目中的图示可知:此圆台是直角梯形转成圆台的条件是:绕垂直于底的腰旋转.
【解答】解:A、是两个圆台,故A错误;
B、上面小下面大,侧面是曲面,故B正确;
C、是一个圆台,故C错误;
D、下面小上面大侧面是曲面,故D错误;
故选:B.
【点评】本题考查直角梯形转成圆台的条件:应绕垂直于底的腰旋转.
3.某同学用牙膏纸盒制作一个如图所示的笔筒,笔筒的筒底为长4.5厘米,宽3.4厘米的矩形.则该笔筒最多能放半径为0.4厘米的圆柱形铅笔( )
A.20支 B.21支 C.22支 D.25支
【分析】此题不能用面积去除面积,而应该用底面长除以直径,再用宽除以直径,用两个商相乘,得出结果.
【解答】解:若按如图方法摆放,
则△ABC为等腰三角形,其高为AD,
则AB=0.8=,BD=0.4+=,
由勾股定理,得AD=≈0.65276,
∵0.8+4×0.65276=3.411>3.4,这种情况不可能,
这样有4个高<2.8+0.4+0.4<3.6,最后还剩下0.9×3.4还可以放4支.
这样,长放0.4+(4个<0.7)+0.4+0.8<4.4<4.5,
宽放4个0.8=3.2<3.4,共4+3+4+3+4+4=22支(如图).
故选:C.
【点评】此处应注意不足0.8厘米放不下一支.
4.如图是由下面五种基本图形中的两种拼接而成,这两种基本图形是( )
A.①⑤ B.②④ C.③⑤ D.②⑤
【分析】根据分割与组合的原理对图形进行分析即解.
【解答】解:分析原图可得:原图由②⑤两种图案组成.
故选:D.
【点评】此题考查了平面图形的分割与组成,主要培养学生的观察能力和空间想象能力.
5.下列图形可以作为一个正方体的展开图的是( )
A. B.
C. D.
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:A、不能作为一个正方体的展开图,故本选项错误;
B、不能作为一个正方体的展开图,故本选项错误;
C、能作为一个正方体的展开图,故本选项正确;
D、不能作为一个正方体的展开图,故本选项错误;
故选:C.
【点评】本题考查了几何体的展开图,属于基础题,注意培养自己的空间想象能力.
6.下列各图经过折叠不能围成一个正方体的是( )
A. B.
C. D.
【分析】由平面图形的折叠及正方体的表面展开图的特点解题.只要有“田”“凹”“一线超过四个正方形”字格的展开图都不是正方体的表面展开图.
【解答】解:A、是正方体的展开图,不符合题意;
B、是正方体的展开图,不符合题意;
C、是正方体的展开图,不符合题意;
D、不是正方体的展开图,缺少一个底面,符合题意.
故选:D.
【点评】本题考查了正方体的展开图,解题时勿忘记四棱柱的特征及正方体展开图的各种情形.
7.如图是一个正方体的展开图,则“数”字的对面的字是( )
A.核 B.心 C.素 D.养
【分析】利用正方体及其表面展开图的特点求解即可.
【解答】解:这是一个正方体的平面展开图,共有六个面,其中“数”字的对面的字是养.
故选:D.
【点评】本题考查了正方体相对两个面上文字的知识,解答本题的关键是从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念.
8.如图,是一个正方体,用一个平面去截这个正方体,截面形状不可能为下图中的( )
A. B.
C. D.
【分析】正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形.因此截面的形状可能是:三角形、四边形、五边形、六边形.
【解答】解:用平面去截正方体,得的截面可能为三角形、四边形、五边形、六边形,不可能为七边形.
故选:D.
【点评】本题考查正方体的截面.正方体的截面的四种情况应熟记.
9.过平面上A、B、C三点中的任意两点作直线,可作( )
A.1条 B.3条 C.1条或3条 D.无数条
【分析】分三点共线和不共线两种情况作出图形,即可得解.
【解答】解:如图,过平面上A、B、C三点中的任意两点作直线,可作1条或3条.
故选C.
【点评】本题考查了直线、射线、线段,要注意分情况讨论,作出图形更形象直观.
10.在开会前,工作人员进行会场布置,如图为工作人员在主席台上由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是( )
A.两点之间线段最短
B.两点确定一条直线
C.垂线段最短
D.过一点可以作无数条直线
【分析】根据直线的性质:两点确定一条直线可得答案.
【解答】解:由两人拉着一条绳子,然后以“准绳”摆放整齐的茶杯,这样做的理由是两点确定一条直线,
故选:B.
【点评】此题主要考查了直线的性质,关键是掌握两点确定一条直线.
二.填空题(共8小题)
11.如图,在长方体ABCD﹣EFGH中,与平面ADHE垂直的棱共有 4 条.
【分析】在长方体,棱与面之间的关系有平行和垂直两种.
【解答】解:与平面ADHE垂直的棱有:AB,DC,HG,EF.共4条.
故答案为4.
【点评】本题考查的知识点为:与一个平面内的一条直线垂直的直线就与这个平面垂直.
12.把一块三角板以一条直角边为轴旋转成的几何体是 圆锥 .
【分析】本题是一块三角板围绕一条直角边为对称轴旋转一周,根据面动成体的原理即可解.
【解答】解:一块三角板以一条直角边为轴旋转成的几何体是圆锥.
【点评】此题考查了立体图形和平面图形的理解能力,主要培养学生的观察能力和空间想象能力.
13.从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为 24 .
【分析】根据几何体表面积的计算公式,从正方体毛坯一角挖去一个小正方体得到的零件的表面积等于原正方体表面积,即可得出答案.
【解答】解:挖去一个棱长为1的小正方体,得到的图形与原图形表面积相等,
则表面积是2×2×6=24.
故答案为:24.
【点评】此题考查了几何体的表面积,本题有多种解法,一种是把每个面的面积计算出来然后相加,这样比较麻烦,另一种算法就是解答中的这种,这种方法的关键是能想象出得到的图形与原图形表面积相等.
14.图中按左侧三个图形阴影部分的特点,将右侧的图形补充完整.
【分析】根据图形中阴影的运动规律即可解,阴影部分是逆时针转动的.
【解答】解:观察图形可知,阴影部分是逆时针转动的,所以右侧的图形是.
故答案为.
【点评】仔细观察图形,找出旋转的规律,是解题的关键.
15.如图是某几何体的表面展开图,则这个几何体是 圆柱体 .
【分析】由平面图形的折叠及立体图形的表面展开图的特点解题.
【解答】解:一个长方形和两个圆折叠后,能围成的几何体是圆柱.
故答案为:圆柱体.
【点评】本题考查了由三视图判断几何体的知识,熟记常见几何体的平面展开图的特征,是解决此类问题的关键.
16.如图,有三张硬纸片,用它们围成一个立体图形叫 圆柱体 .
【分析】利用已知图形结合三视图的有关知识,可以判断出它所组成的图形.
【解答】解:利用三视图有关知识,矩形只能组成圆柱形,两个圆正好组成圆柱的上底与下底.
故填:圆柱体
【点评】此题主要考查了三视图有关知识,以及考查同学们的立体思维.
17.如图是每个面上都有一个汉字的正方体的一种展开图,那么在正方体的表面与“生”相对应的面上的汉字是 学 .
【分析】正方体的表面展开图,相对的面之间一定相隔一个正方形,根据这一特点作答.
【解答】解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“生”与“学”是相对面.
故答案为:学.
【点评】本题主要考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
18.用一个平面截下列几何体:①长方体,②六棱柱,③球,④圆柱,⑤圆锥,截面能得到三角形的是 ①②⑤ (填写序号即可)
【分析】根据用一个平面截一个几何体得到的面叫做几何体的截面,利用常见图形分析得出即可.
【解答】解:①长方体能截出三角形;
②六棱柱沿对角线截几何体可以截出三角形;
③球不能截出三角形;
④圆柱不能截出三角形;
⑤圆锥能截出三角形;
故截面可能是三角形的有①②⑤共3个.
故答案为:①②⑤.
【点评】本题考查几何体的截面,截面的形状既与被截的几何体有关,还与截面的角度和方向有关.
三.解答题(共8小题)
19.如图,上面是一些具体的物体,下面是一些立体图形,试找出与下面立体图形相类似的实物(用线连接).
【分析】结合给出事物的特征,抽象出所对应的立体图形,关键是运用空间想象能力.
【解答】解:埃及金字塔﹣﹣(2)
西瓜﹣﹣(3)
水杯﹣﹣(1)
房屋﹣﹣(5).
【点评】本题要掌握常见立体图形的特征,注意培养观察力和空间想象能力.
20.已知长方形的长为4cm.宽为3cm,将其绕它的一边所在的直线旋转一周,得到一个几何体,
(1)求此几何体的体积;
(2)求此几何体的表面积.(结果保留π)
【分析】(1)旋转后的几何体是圆柱体,先确定出圆柱的底面半径和高,再根据圆柱的体积公式计算即可求解;
(2)根据圆柱的表面积公式计算即可求解.
【解答】解:长方形绕一边旋转一周,得圆柱.
(1)情况①:π×32×4=36π(cm3);
情况②:π×42×3=48π(cm3);
(2)情况①:
π×3×2×4+π×32×2
=24π+18π
=42π(cm2);
情况②:
π×4×2×3+π×42×2
=24π+32π
=56π(cm2).
【点评】本题主要考查的是点、线、面、体,根据图形确定出圆柱的底面半径和高的长是解题的关键.
21.六盒磁带按“规则方式”打包,所谓“规则方式”是指每相邻两盒必须以完全一样的面对接,最后得到的包装形状是一个长方形.已知磁带盒的大小为abc=11×7×2(单位cm).
(1)请画出示意图,给出一种打包方式,使其表面积最小;
(2)若不给出a、b、c的具体尺寸,只假定a≥b≥c,3问能否按照已知的方式打包,使其表面积最小?并说明理由.
【分析】一盒火柴的图形如图甲所示,则三个面的面积记为A=bc,B=ac,C=ab;考虑到6盒火柴,6=1×6=2×3,因此,规则方式打包有两类:“1×6”和“2×3”.(1)已知磁带盒的大小为abc=11×7×2,分别求出两种方式的表面积,比较大小即可;(2)已知a≥b≥c,可设a=46mm,b=36mm,c=16mm,分别求出两种方式的表面积,比较大小即可.
【解答】解:(1)设:三个面的面积记为A=bc,B=ac,C=ab,
①在1×6的方式下,打包方式如图乙,这时,表面积
S乙=2C+12B+12A=2×11×7+12×11×2+12×7×2=586(cm2);
②在2×3的方式下,打包方式如图丙,这时,表面积
S丙=4C+6B+12A=4×11×7+6×11×2+12×7×2=608(cm2);
因为S乙<S丙,所以最小表面积的打包方式是1×6.
(2)若a≥b≥c,则单叠(即1*6方式)打包的最小表面积S=2ab+12ac+12bc;
双叠(即2*3方式)打包最小表面积S'=4ab+6ac+12bc.所以S﹣S'=2a(3c﹣b).
所以:当a≥b,且c≤b<3c时,最小表面积为双叠
当a≥b>3c时,最小表面积为单叠
当a≥b=3c时,两种方式一样大
【点评】此题考查了平面图形的有关知识,培养学生的观察能力和图形的组合能力;注意其中的一个面被上面的立方体覆盖.
22.对于如图①、②、③、④所示的四个平面图
我们规定:如图③,它的顶点为A、B、C、D、E共5个,区域为AED、ABE、BEC、CED共4个,边为AE、EC、DE、EB、AB、BC、CD、DA共8条.
(1)按此规定将图①、②、④的顶点①数、边数、区域数填入下列表格:
图 顶点数 边数 区域数
①
②
③ 5 8 4
④
(2)观察上表,请你归纳上述平面图的顶点数、边数、区域数之间的数量关系.
(3)若有一个平面图满足(2)中归纳所得的数量关系,它共有9个区域,且每一个顶点出发都有3条边,则这个平面图共有多少条边?
【分析】(1)根据规定结合图形即可填充表格.
(2)根据所填的表格即可得出平面图的顶点数、边数、区域数之间的数量关系.
(3)根据(2)的关系直接写出答案.
【解答】解:(1)按此规定将图①、②、④的顶点数、边数、区域数填入下列表格:
图 顶点数 边数 区域数
① 4 6 3
② 6 9 4
③ 5 8 4
④ 10 15 6
(2)由表格得:顶点数+区域数=边数+1,
(3)设顶点数为x,根据题意可知,x+9=+1,
得出x=16
每个顶点发出三个3边,有9个区域数,
则有16个顶点,24条边.
【点评】本题考查平面图形的知识,有一定难度,关键是理解题意,根据特殊推出一般规律.
23.如图,在无阴影的方格中选出两个画出阴影,使它们与图中4个有阴影的正方形一起可以构成一个正方体的表面展开图.(在图1和图2中任选一个进行解答,只填出一种答案即可)
【分析】和一个正方体的平面展开图相比较,可得出一个正方体11种平面展开图.
【解答】解:只写出一种答案即可.(4分)
图1:
图2:
【点评】正方体共有11种表面展开图,把11种展开图都去掉一个面得无盖的正方体展开图,把相同的归为一种得无盖正方体有8种表面展开图.
24.正方体是由六个平面图形围成的立体图形,设想沿着正方体的一些棱将它剪开,就可以把正方体剪成一个平面图形,但同一个正方体,按不同的方式展开所得的平面展开图是不一样的,下面的图形是由6个大小一样的正方形,拼接而成的,请问这些图形中哪些可以折成正方体?试试看.
【分析】由平面图形的折叠及正方体的展开图解题.
【解答】解:由图示可知:图1,图2,图3,图4,图6,图10,图11,图12均可以折成正方体.
【点评】解题时勿忘记四棱柱的特征及正方体展开图的各种情形.注意有田字的不能展开成正方体.
25.如图是一个正方体盒子的展开图,要把﹣8、10、﹣12、8、﹣10、12些数字分别填入六个小正方形,使得按虚线折成的正方体相对面上的两个数相加得0.
【分析】先根据正方体及其表面展开图的特点,找到相对的面,再相加得0的两个数填入即可.
【解答】解:﹣8和8,﹣12和12,﹣10和10互为相反数,
所作图形如下:
.
【点评】本题考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题.
26.用平面截几何体可得到平面图形,在表示几何体的字母后填上它可截出的平面图形的号码.
如A(1、5、6);则B( 1,3,4 );C( 1,2,3,4 );D( 5 );E( 3,5,6 ).
【分析】分别分析其余四种图形的所有的截面情况,再写出答案.
【解答】解:B三棱锥,截面有可能是三角形,正方形,梯形
C正方体,截面有可能是三角形,四边形(矩形,正方形,梯形),五边形,六边形
D球体,截面只可能是圆
E圆柱体,截面有可能是椭圆,圆,矩形,
因此应该写B(1、3、4);C(1、2、3、4);D(5);E(3、5、6).
【点评】截面的形状既与被截的几何体有关,还与截面的角度和方向有关.对于这类题,最好是动手动脑相结合,亲自动手做一做,从中学会分析和归纳的思想方法.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
