2019-2020学年青岛新版上册数学七年级《第5章 代数式与函数的初步认识》单元测试卷(解析版)
文档属性
| 名称 | 2019-2020学年青岛新版上册数学七年级《第5章 代数式与函数的初步认识》单元测试卷(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 287.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 13:36:18 | ||
图片预览




文档简介
2020年青岛新版上册数学七年级《第5章 代数式与函数的初步认识》单元测试卷
一.选择题(共10小题)
1.以下代数式书写规范的是( )
A.(a+b)×2 B. C. D.x+y厘米
2.下列关于“代数式3x+2y”的意义叙述不正确的有( )个.
①x的3倍加上y的2倍的和;②小明跑步速度为x千米/小时,步行的速度为y千米/时,则小明跑步3小时后步行2小时,走了(3x+2y)千米;③某小商品以每个3元卖了x个,又以每个2元卖了y个,则共卖了(3x+2y)元.
A.3 B.2 C.1 D.0
3.买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要( )
A.(4m+7n)元 B.28mn元 C.(7m+4n)元 D.11mn元
4.元旦,是公历新一年的第一天.“元旦”一词最早出现于《晋书》:“颛帝以孟夏正月为元,其实正朔元旦之春”.中国古代曾以腊月、十月等的月首为元旦.1949年中华人民共和国以公历1月1日为元旦,因此元旦在中国也被称为“阳历年”.为庆祝元旦,人民商场举行促销活动,促销的方法是“消费超过100元时,所购买的商品按原价打8折后,再减少20元”.若某商品的原价为x元(x>100),则购买该商品实际付款的金额(单位:元)是( )
A.80%x﹣20 B.80%(x﹣20) C.20%x﹣20 D.20%(x﹣20)
5.在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码、有一种密码,将英文26个字母a,b,c…,z(不论大小写)依次对应1,2,3,…,26这26个自然数.当明码字母对应的序号x为奇数时,密码字母对应的序号是;当明码字母对应的序号x为偶数时,密码字母对应的序号是+14.按上述规定,将明码“hope”译成密码是( )
字母 a b c d e f g h i j k l m
序号 1 2 3 4 5 6 7 8 9 10 11 12 13
字母 n o p q r s t u v w x y z
序号 14 15 16 17 18 19 20 21 22 23 24 25 26
A.gawq B.rivd C.gihe D.hope
6.小邢到单位附近的加油站加油,如图是小邢所用的加油机上的数据显示牌,则数据中的变量是( )
A.金额 B.数量 C.单价 D.金额和数量
7.下列关系式中,不是函数关系的是( )
A.y=(x<0) B.y=±(x>0) C.y=(x>0) D.y=﹣(x>0)
8.汽车离开甲站10千米后,以60千米/时的速度匀速前进了t小时,则汽车离开甲站所走的路程s(千米)与时间t(小时)之间的关系式是( )
A.s=10+60t B.s=60t C.s=60t﹣10 D.s=10﹣60t
9.函数y=的自变量x的取值范围是( )
A.x>1 B.x<1 C.x≤1 D.x≥1
10.某地海拔高度h与温度T的关系可用T=21﹣6h来表示(其中温度单位℃,海拔高度单位为千米),则该地区某海拔高度为2000米的山顶上的温度为( )
A.15℃ B.9℃ C.3℃ D.7℃
二.填空题(共8小题)
11.代数式6a2的实际意义: .
12.一台电脑原价a元,降低m元后,又降价20%,现售价为 元.
13.如果代数式﹣2a2+3b+8的值为1,那么代数式4a2﹣6b+2的值等于 .
14.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2019的值为 .
15.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中, 随 变化而变化,其中自变量是 ,因变量是 .
16.如图,在△ABC中,∠C=90°,AC=8,BC=6,D点在AC上运动,设AD长为x,△BCD的面积y,则y与x之间的函数表达式为 .
17.函数y=中,自变量x的取值范围是 .
18.已知变量y与x的关系式是,则当x=2时,y= .
三.解答题(共8小题)
19.请将下列代数式进行分类(至少三种以上)
,a,3x,,,,a2+x,4x2ay,x+8.
20.小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含m,n的代数式表示地面的总面积S;
(2)已知n=1.5,且客厅面积是卫生间面积的8倍,如果铺1平方米地砖的平均费用为100元,那么小王铺地砖的总费用为多少元?
21.某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动.活动期间向客户提供两种优惠方案.
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x条(x>20).
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法和所需费用.
22.一种树苗的高度与生长年数之间的关系如下表所示(树高原高100cm)
(1)填出第四年树苗可能达到的高度;
(2)请用含x的代数式表示高度h;
(3)用你得到的代数式求生长了8年后的树苗可能达到的高度
23.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
24.阅读下面材料,再回答问题.
一般地,如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=f(x).那么y=f(x)就叫偶函数.如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=﹣f(x).那么y=f(x)就叫奇函数.
例如:f(x)=x4
当x取任意实数时,f(﹣x)=(﹣x)4=x4∴f(﹣x)=f(x)∴f(x)=x4是偶函数.
又如:f(x)=2x3﹣x.
当x取任意实数时,∵f(﹣x)=2(﹣x)3﹣(﹣x)=﹣2x3+x=﹣(2x3﹣x)∴f(﹣x)=﹣f(x)∴f(x)=2x3﹣x是奇函数.
问题1:下列函数中:①y=x2+1②③④⑤y=x﹣2﹣2|x|
是奇函数的有 ;是偶函数的有 (填序号)
问题2:仿照例证明:函数④或⑤是奇函数还是偶函数(选择其中之一)
25.“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=280(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
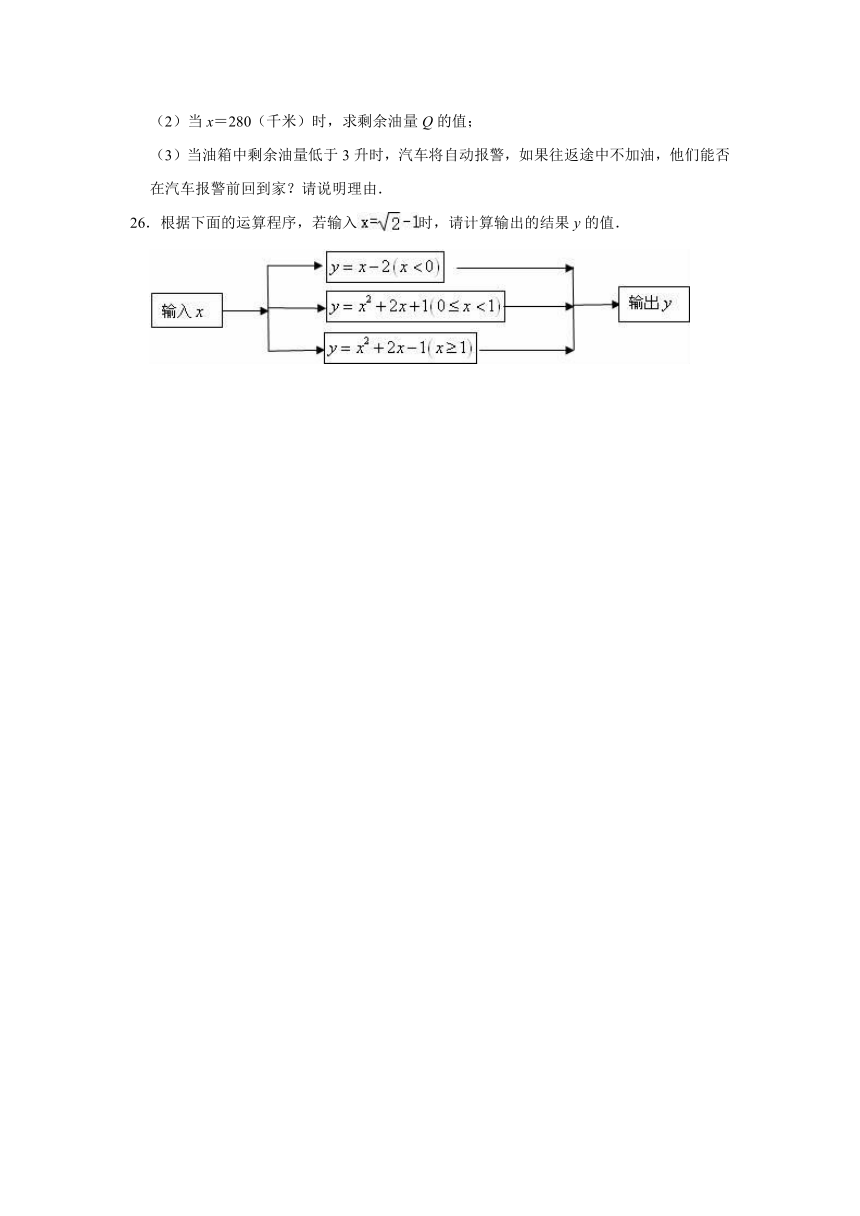
26.根据下面的运算程序,若输入时,请计算输出的结果y的值.
2020年青岛新版上册数学七年级《第5章 代数式与函数的初步认识》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.以下代数式书写规范的是( )
A.(a+b)×2 B. C. D.x+y厘米
【分析】根据代数式的书写要求判断各项.
【解答】解:A、正确的书写是2(a+b);
B、书写规范;
C、应把带分数写成假分数;
D、应用括号把代数式括起来.
故选:B.
【点评】代数式的书写要求:
(1)在代数式中出现的乘号,通常简写成“?”或者省略不写;
(2)数字与字母相乘时,数字要写在字母的前面;
(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分数的形式.
2.下列关于“代数式3x+2y”的意义叙述不正确的有( )个.
①x的3倍加上y的2倍的和;②小明跑步速度为x千米/小时,步行的速度为y千米/时,则小明跑步3小时后步行2小时,走了(3x+2y)千米;③某小商品以每个3元卖了x个,又以每个2元卖了y个,则共卖了(3x+2y)元.
A.3 B.2 C.1 D.0
【分析】按照代数式的意义和运算顺序判断各项.
【解答】解:“代数式3x+2y”的意义是x的3倍加上y的2倍的和,故①正确;
将“代数式3x+2y”赋予实际意义,可以是小明跑步速度为x千米/小时,步行的速度为y千米/时,则小明跑步3小时后步行2小时,走了(3x+2y)千米,故②正确;
还可以是某小商品以每个3元卖了x个,又以每个2元卖了y个,则共卖了(3x+2y)元,故③正确.
故不正确的有0个.
故选:D.
【点评】此类问题应结合实际,根据代数式的特点解答.注意掌握代数式的意义.
3.买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要( )
A.(4m+7n)元 B.28mn元 C.(7m+4n)元 D.11mn元
【分析】用4个足球的价钱加上7个篮球的价钱即可.
【解答】解:买4个足球、7个篮球共需要(4m+7n)元.
故选:A.
【点评】此题考查列代数式,找出题目蕴含的数量关系是解决问题的关键.
4.元旦,是公历新一年的第一天.“元旦”一词最早出现于《晋书》:“颛帝以孟夏正月为元,其实正朔元旦之春”.中国古代曾以腊月、十月等的月首为元旦.1949年中华人民共和国以公历1月1日为元旦,因此元旦在中国也被称为“阳历年”.为庆祝元旦,人民商场举行促销活动,促销的方法是“消费超过100元时,所购买的商品按原价打8折后,再减少20元”.若某商品的原价为x元(x>100),则购买该商品实际付款的金额(单位:元)是( )
A.80%x﹣20 B.80%(x﹣20) C.20%x﹣20 D.20%(x﹣20)
【分析】根据题意可以用相应的代数式表示购买该商品实际付款的金额.
【解答】解:由题意可得,若某商品的原价为x元(x>100),
则购买该商品实际付款的金额是:80%x﹣20(元),
故选:A.
【点评】本题考查列代数式,解答本题的关键明确题意,列出相应的代数式.
5.在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码、有一种密码,将英文26个字母a,b,c…,z(不论大小写)依次对应1,2,3,…,26这26个自然数.当明码字母对应的序号x为奇数时,密码字母对应的序号是;当明码字母对应的序号x为偶数时,密码字母对应的序号是+14.按上述规定,将明码“hope”译成密码是( )
字母 a b c d e f g h i j k l m
序号 1 2 3 4 5 6 7 8 9 10 11 12 13
字母 n o p q r s t u v w x y z
序号 14 15 16 17 18 19 20 21 22 23 24 25 26
A.gawq B.rivd C.gihe D.hope
【分析】观察可看出,我们需要对所求明码式进行整理然后利用对应代数式代入求得密码序号,再确定其对应字母求解.
【解答】解:根据题意,得h对应的序号是8,则密码对应的序号应是18,即r;
o对应的序号是15,即密码对应的序号是9,即i;
p对应的序号是16,即密码对应的序号是22,即v;
e对应的序号是5,即密码对应的序号是4,即d.
故选:B.
【点评】能够首先说出明码字母对应的序号,再根据定义计算密码对应的序号,进一步确定其对应的字母.
6.小邢到单位附近的加油站加油,如图是小邢所用的加油机上的数据显示牌,则数据中的变量是( )
A.金额 B.数量 C.单价 D.金额和数量
【分析】根据常量与变量的定义即可判断.
【解答】解:常量是固定不变的量,变量是变化的量,
单价是不变的量,而金额是随着数量的变化而变化,
故选:D.
【点评】本题考查常量与变量,解题的关键是正确理解常量与变量,本题属于基础题型.
7.下列关系式中,不是函数关系的是( )
A.y=(x<0) B.y=±(x>0) C.y=(x>0) D.y=﹣(x>0)
【分析】在运动变化过程中,有两个变量x和y,对于x的每一个值y都有唯一确定的值与之对应,那么y是x的函数,x是自变量.
【解答】解:A当x<0时,对于x的每一个值,y=都有唯一确定的值,所以y=(x<0)是函数.
B当x>0时,对于x的每一个值,y=±有两个互为相反数的值,而不是唯一确定的值,所以y=±(x>0)不是函数.
C当x>0时,对于x的每一个值,y=都有唯一确定的值,所以y=(x>0)是函数.
D当x>0时,对于x的每一个值,y=﹣都有唯一确定的值,所以y=﹣(x>0)是函数.
故选:B.
【点评】准确理解函数的概念,用函数的概念作出正确的判断.
8.汽车离开甲站10千米后,以60千米/时的速度匀速前进了t小时,则汽车离开甲站所走的路程s(千米)与时间t(小时)之间的关系式是( )
A.s=10+60t B.s=60t C.s=60t﹣10 D.s=10﹣60t
【分析】根据路程与时间的关系,可得函数解析式.
【解答】解:s=10+60t,
故选:A.
【点评】本题考查了函数关系式,注意先行驶了10千米,路程等于先行驶的加上匀速行驶.
9.函数y=的自变量x的取值范围是( )
A.x>1 B.x<1 C.x≤1 D.x≥1
【分析】根据二次根式的意义,被开方数是非负数.
【解答】解:根据题意得x﹣1≥0,
解得x≥1.
故选:D.
【点评】本题考查了函数自变量的取值范围的确定和分式的意义.函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负数.
10.某地海拔高度h与温度T的关系可用T=21﹣6h来表示(其中温度单位℃,海拔高度单位为千米),则该地区某海拔高度为2000米的山顶上的温度为( )
A.15℃ B.9℃ C.3℃ D.7℃
【分析】把h=2000米=2千米代入T=21﹣6h即得.
【解答】解:2000米=2千米,
T=21﹣6h=21﹣6×2=9℃.
故选:B.
【点评】本题考查函数值的知识,根据题目的信息代入运算即可.
二.填空题(共8小题)
11.代数式6a2的实际意义: 棱长为a的正方体的表面积 .
【分析】从正方体的表面积考虑求解.
【解答】解:代数式6a2表示的实际意义:棱长为a的正方体的表面积.
故答案为:棱长为a的正方体的表面积.
【点评】本题考查代数式的意义问题,对式子进行分析,弄清各项间的关系即可.
12.一台电脑原价a元,降低m元后,又降价20%,现售价为 0.8(a﹣m) 元.
【分析】先表示出降价m元的,然后表示出降价20%的即可.
【解答】解:a元降价m元为(a﹣m)元,
降价20%后为(a﹣m)(1﹣20%)=0.8(a﹣m),
故答案为:0.8(a﹣m).
【点评】本题考查了列代数式的知识,解题的关键是表示出分别表示出两次降价的量,难度不大.
13.如果代数式﹣2a2+3b+8的值为1,那么代数式4a2﹣6b+2的值等于 16 .
【分析】根据﹣2a2+3b+8的值为1,可得:﹣2a2+3b+8=1,所以﹣2a2+3b=﹣7,据此求出代数式4a2﹣6b+2的值等于多少即可.
【解答】解:∵﹣2a2+3b+8的值为1,
∴﹣2a2+3b+8=1,
∴﹣2a2+3b=﹣7,
∴4a2﹣6b+2
=﹣2(﹣2a2+3b)+2
=﹣2×(﹣7)+2
=14+2
=16
故答案为:16.
【点评】此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.
14.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2019的值为 ﹣1009 .
【分析】根据条件求出前几个数的值,再分n是奇数时,结果等于﹣(n﹣1),n是偶数时,结果等于﹣,然后把n的值代入进行计算即可得解.
【解答】解:a1=0,
a2=﹣|a1+1|=﹣|0+1|=﹣1,
a3=﹣|a2+2|=﹣|﹣1+2|=﹣1,
a4=﹣|a3+3|=﹣|﹣1+3|=﹣2,
a5=﹣|a4+4|=﹣|﹣2+4|=﹣2,
a6=﹣|a5+5|=﹣|﹣2+5|=﹣3,
a7=﹣|a6+6|=﹣|﹣3+6|=﹣3,
…,
所以,n是奇数时,an=﹣(n﹣1),n是偶数时,an=﹣,
∴a2019=﹣(2019﹣1)=﹣1009.
故答案为:﹣1009.
【点评】此题主要考查了数字变化规律,根据所求出的数,观察出n为奇数与偶数时的结果的变化规律是解题的关键.
15.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中, 温度 随 时间 变化而变化,其中自变量是 时间 ,因变量是 温度 .
【分析】根据函数的定义:对于函数中的每个值x,变量y按照一定的法则有一个确定的值y与之对应;来解答即可.
【解答】解:“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,温度随时间变化而变化,其中自变量是:时间,因变量是:温度.
故答案是:温度、时间、时间、温度.
【点评】函数的定义:设x和y是两个变量,D是实数集的某个子集,若对于D中的每个值x,变量y按照一定的法则有一个确定的值y与之对应,称变量y为变量x的函数,记作y=f(x);变量是指在程序的运行过程中随时可以发生变化的量.
16.如图,在△ABC中,∠C=90°,AC=8,BC=6,D点在AC上运动,设AD长为x,△BCD的面积y,则y与x之间的函数表达式为 y=24﹣3x .
【分析】根据三角形的面积=×底×高,结合BC=6,CD=(8﹣x),即可得到,△BCD的面积y与AD的长之间的函数表达式.
【解答】解:根据题意得:
CD的长为:8﹣x,
则y=×6(8﹣x)=24﹣3x,
即y与x之间的函数表达式为:y=24﹣3x.
【点评】本题考查了函数关系式,正确掌握三角形的面积公式是解题的关键.
17.函数y=中,自变量x的取值范围是 x≥2 .
【分析】根据二次根式的性质,被开方数大于等于0,就可以求解.
【解答】解:依题意,得x﹣2≥0,
解得:x≥2,
故答案为:x≥2.
【点评】本题主要考查函数自变量的取值范围,考查的知识点为:二次根式的被开方数是非负数.
18.已知变量y与x的关系式是,则当x=2时,y= ﹣4 .
【分析】将x=2代入y与x的关系式中求解即可.
【解答】解:将x=2代入,
可得:y=3×2﹣×4=6﹣10=﹣4.
故答案为:﹣4.
【点评】本题考查了函数值的知识,当已知函数解析式时,求函数值就是求代数式的值.
三.解答题(共8小题)
19.请将下列代数式进行分类(至少三种以上)
,a,3x,,,,a2+x,4x2ay,x+8.
【分析】根据代数式的分类解答:.
【解答】解:本题答案不唯一.
单项式:,a,3x,4x2ay;
多项式:,a2+x,x+8;
整式:,a,3x,4x2ay,,a2+x,x+8;
分式:.
【点评】本题考查了代数式的定义及其分类.由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子,或含有字母的数学表达式称为代数式.注意,分式和无理式都不属于整式.
20.小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含m,n的代数式表示地面的总面积S;
(2)已知n=1.5,且客厅面积是卫生间面积的8倍,如果铺1平方米地砖的平均费用为100元,那么小王铺地砖的总费用为多少元?
【分析】(1)根据总面积等于四个部分矩形的面积之和列式整理即可得解;
(2)根据题意求出m的值,把m,n的值代入计算即可.
【解答】解:(1)S=2n+6m+3×4+2×3=6m+2n+18.
(2)n=1.5时2n=3
根据题意,得6m=8×3=24,
∵铺1平方米地砖的平均费用为100元,
∴铺地砖的总费用为:
100(6m+2n+18)=100×(24+3+18)=4500.
答:铺地砖的总费用4500元.
【点评】此题考查了列代数式,准确表示出各部分矩形的长和宽是解题的关键.
21.某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动.活动期间向客户提供两种优惠方案.
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x条(x>20).
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法和所需费用.
【分析】(1)根据题目提供的两种不同的付款方式列出代数式即可;
(2)将x=30分别代入求得的代数式中即可得到方案一和二的费用,然后比较即可得到选择哪种方案更合算;
(3)根据题意考虑可以先按方案一购买20套西装获赠送20条领带,再按方案二购买10条领带更合算.
【解答】解:(1)方案一购买,需付款:20×200+40(x﹣20)=40x+3200(元),
按方案二购买,需付款:0.9(20×200+40x)=3600+36x(元);
(2)把x=30分别代入:40x+3200=4×30+3200=4400(元),
3600+36×30=4680(元).
因为4400<4680,所以按方案一购买更合算;
(3)先按方案一购买20套西装(送20条领带),再按方案二购买(x﹣20)条领带,共需费用:
20×200+0.9×40(x﹣20)=36x+3280,
当x=30时,36×30+3280=4360(元).
【点评】本题考查了列代数式和求代数式的值的相关的题目,解题的关键是认真分析题目并正确的列出代数式.
22.一种树苗的高度与生长年数之间的关系如下表所示(树高原高100cm)
(1)填出第四年树苗可能达到的高度;
(2)请用含x的代数式表示高度h;
(3)用你得到的代数式求生长了8年后的树苗可能达到的高度
【分析】(1)通过对表格中的数据分析,可知从第二年开始,树苗高度每年增加25cm.因此,第四年树苗高度是在第一年的基础上加3个25.
(2)根据规律可推出第x年树苗的高度h=125+25×(x﹣1);
(3)将数字8代入上面代数式计算即可.
【解答】解:(1)依题意有:第1年是125cm;
第2年是150=(125+25×1)cm;
第3年是175=(125+25×2)cm;
第4年是125+25×3=200cm.
(2)根据规律可得:第x年树苗的高度h=125+25×(x﹣1)=25x+100;所以h=25x+100.
(3)第8年后树苗可能达到的高度为:25×8+100=300cm.
【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键是从第二年开始,逐年增加25cm.
23.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
【分析】根据总价=单价×数量,可得函数关系式.
【解答】解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
【点评】主要考查了常量与变量.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
24.阅读下面材料,再回答问题.
一般地,如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=f(x).那么y=f(x)就叫偶函数.如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=﹣f(x).那么y=f(x)就叫奇函数.
例如:f(x)=x4
当x取任意实数时,f(﹣x)=(﹣x)4=x4∴f(﹣x)=f(x)∴f(x)=x4是偶函数.
又如:f(x)=2x3﹣x.
当x取任意实数时,∵f(﹣x)=2(﹣x)3﹣(﹣x)=﹣2x3+x=﹣(2x3﹣x)∴f(﹣x)=﹣f(x)∴f(x)=2x3﹣x是奇函数.
问题1:下列函数中:①y=x2+1②③④⑤y=x﹣2﹣2|x|
是奇函数的有 ②④ ;是偶函数的有 ①⑤ (填序号)
问题2:仿照例证明:函数④或⑤是奇函数还是偶函数(选择其中之一)
【分析】(1)根据题目信息,求出f(﹣x)的值,如果f(﹣x)=f(x),则是偶函数,如果f(﹣x)=﹣f(x),则是奇函数;
(2)同(1)的思路进行计算即可证明.
【解答】解:问题1:①y=(﹣x)2+1=x2+1,
∴①是偶函数;
②y==﹣,
∴②是奇函数;
③y=≠≠﹣,
∴③既不是奇函数,也不是偶函数;
④y=﹣x+=﹣(x+),
∴④是奇函数;
⑤y=(﹣x)﹣2﹣2|﹣x|=x﹣2﹣2|x|,
∴⑤是偶函数,
故答案为:奇函数有②④;偶函数有①⑤;
问题2:证明:④∵当x≠0时,
f(﹣x)=﹣x+=﹣(x+)=﹣f(x),
∴y=x+是奇函数,
⑤∵f(﹣x)=(﹣x)﹣2﹣2|﹣x|=x﹣2﹣2|x|=f(x),
∴y=x﹣2﹣2|x|是偶函数.
【点评】本题考查了奇函数与偶函数的定义,根据题目提供信息,看懂题意准确找出题目的解题思路是解题的关键.
25.“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=280(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
【分析】(1)根据平均每千米的耗油量=总耗油量÷行驶路程即可得出该车平均每千米的耗油量,再根据剩余油量=总油量﹣平均每千米的耗油量×行驶路程即可得出Q关于x的函数关系式;
(2)代入x=280求出Q值即可;
(3)根据行驶的路程=耗油量÷平均每千米的耗油量即可求出报警前能行驶的路程,与景点的往返路程比较后即可得出结论.
【解答】解:(1)该车平均每千米的耗油量为(45﹣30)÷150=0.1(升/千米),
行驶路程x(千米)与剩余油量Q(升)的关系式为Q=45﹣0.1x;
(2)当x=280时,Q=45﹣0.1×280=17(L).
答:当x=280(千米)时,剩余油量Q的值为17L.
(3)(45﹣3)÷0.1=420(千米),
∵420>400,
∴他们能在汽车报警前回到家.
【点评】本题考查了函数的关系式以及一次函数图象上点的坐标特征,根据数量关系列出函数关系式是解题的关键.
26.根据下面的运算程序,若输入时,请计算输出的结果y的值.
【分析】先判断出﹣1的范围,然后根据分段函数解析式,代入相应的解析式进行计算即可求解.
【解答】解:∵0<﹣1<1,
∴输入x=﹣1,
可得y=x2+2x+1=(x+1)2=(﹣1+1)2=2.
故答案为:2.
【点评】本题考查了求函数值,根据x的大小确定出进行计算的函数解析式是解题的关键.
一.选择题(共10小题)
1.以下代数式书写规范的是( )
A.(a+b)×2 B. C. D.x+y厘米
2.下列关于“代数式3x+2y”的意义叙述不正确的有( )个.
①x的3倍加上y的2倍的和;②小明跑步速度为x千米/小时,步行的速度为y千米/时,则小明跑步3小时后步行2小时,走了(3x+2y)千米;③某小商品以每个3元卖了x个,又以每个2元卖了y个,则共卖了(3x+2y)元.
A.3 B.2 C.1 D.0
3.买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要( )
A.(4m+7n)元 B.28mn元 C.(7m+4n)元 D.11mn元
4.元旦,是公历新一年的第一天.“元旦”一词最早出现于《晋书》:“颛帝以孟夏正月为元,其实正朔元旦之春”.中国古代曾以腊月、十月等的月首为元旦.1949年中华人民共和国以公历1月1日为元旦,因此元旦在中国也被称为“阳历年”.为庆祝元旦,人民商场举行促销活动,促销的方法是“消费超过100元时,所购买的商品按原价打8折后,再减少20元”.若某商品的原价为x元(x>100),则购买该商品实际付款的金额(单位:元)是( )
A.80%x﹣20 B.80%(x﹣20) C.20%x﹣20 D.20%(x﹣20)
5.在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码、有一种密码,将英文26个字母a,b,c…,z(不论大小写)依次对应1,2,3,…,26这26个自然数.当明码字母对应的序号x为奇数时,密码字母对应的序号是;当明码字母对应的序号x为偶数时,密码字母对应的序号是+14.按上述规定,将明码“hope”译成密码是( )
字母 a b c d e f g h i j k l m
序号 1 2 3 4 5 6 7 8 9 10 11 12 13
字母 n o p q r s t u v w x y z
序号 14 15 16 17 18 19 20 21 22 23 24 25 26
A.gawq B.rivd C.gihe D.hope
6.小邢到单位附近的加油站加油,如图是小邢所用的加油机上的数据显示牌,则数据中的变量是( )
A.金额 B.数量 C.单价 D.金额和数量
7.下列关系式中,不是函数关系的是( )
A.y=(x<0) B.y=±(x>0) C.y=(x>0) D.y=﹣(x>0)
8.汽车离开甲站10千米后,以60千米/时的速度匀速前进了t小时,则汽车离开甲站所走的路程s(千米)与时间t(小时)之间的关系式是( )
A.s=10+60t B.s=60t C.s=60t﹣10 D.s=10﹣60t
9.函数y=的自变量x的取值范围是( )
A.x>1 B.x<1 C.x≤1 D.x≥1
10.某地海拔高度h与温度T的关系可用T=21﹣6h来表示(其中温度单位℃,海拔高度单位为千米),则该地区某海拔高度为2000米的山顶上的温度为( )
A.15℃ B.9℃ C.3℃ D.7℃
二.填空题(共8小题)
11.代数式6a2的实际意义: .
12.一台电脑原价a元,降低m元后,又降价20%,现售价为 元.
13.如果代数式﹣2a2+3b+8的值为1,那么代数式4a2﹣6b+2的值等于 .
14.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2019的值为 .
15.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中, 随 变化而变化,其中自变量是 ,因变量是 .
16.如图,在△ABC中,∠C=90°,AC=8,BC=6,D点在AC上运动,设AD长为x,△BCD的面积y,则y与x之间的函数表达式为 .
17.函数y=中,自变量x的取值范围是 .
18.已知变量y与x的关系式是,则当x=2时,y= .
三.解答题(共8小题)
19.请将下列代数式进行分类(至少三种以上)
,a,3x,,,,a2+x,4x2ay,x+8.
20.小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含m,n的代数式表示地面的总面积S;
(2)已知n=1.5,且客厅面积是卫生间面积的8倍,如果铺1平方米地砖的平均费用为100元,那么小王铺地砖的总费用为多少元?
21.某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动.活动期间向客户提供两种优惠方案.
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x条(x>20).
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法和所需费用.
22.一种树苗的高度与生长年数之间的关系如下表所示(树高原高100cm)
(1)填出第四年树苗可能达到的高度;
(2)请用含x的代数式表示高度h;
(3)用你得到的代数式求生长了8年后的树苗可能达到的高度
23.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
24.阅读下面材料,再回答问题.
一般地,如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=f(x).那么y=f(x)就叫偶函数.如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=﹣f(x).那么y=f(x)就叫奇函数.
例如:f(x)=x4
当x取任意实数时,f(﹣x)=(﹣x)4=x4∴f(﹣x)=f(x)∴f(x)=x4是偶函数.
又如:f(x)=2x3﹣x.
当x取任意实数时,∵f(﹣x)=2(﹣x)3﹣(﹣x)=﹣2x3+x=﹣(2x3﹣x)∴f(﹣x)=﹣f(x)∴f(x)=2x3﹣x是奇函数.
问题1:下列函数中:①y=x2+1②③④⑤y=x﹣2﹣2|x|
是奇函数的有 ;是偶函数的有 (填序号)
问题2:仿照例证明:函数④或⑤是奇函数还是偶函数(选择其中之一)
25.“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=280(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
26.根据下面的运算程序,若输入时,请计算输出的结果y的值.
2020年青岛新版上册数学七年级《第5章 代数式与函数的初步认识》单元测试卷
参考答案与试题解析
一.选择题(共10小题)
1.以下代数式书写规范的是( )
A.(a+b)×2 B. C. D.x+y厘米
【分析】根据代数式的书写要求判断各项.
【解答】解:A、正确的书写是2(a+b);
B、书写规范;
C、应把带分数写成假分数;
D、应用括号把代数式括起来.
故选:B.
【点评】代数式的书写要求:
(1)在代数式中出现的乘号,通常简写成“?”或者省略不写;
(2)数字与字母相乘时,数字要写在字母的前面;
(3)在代数式中出现的除法运算,一般按照分数的写法来写.带分数要写成假分数的形式.
2.下列关于“代数式3x+2y”的意义叙述不正确的有( )个.
①x的3倍加上y的2倍的和;②小明跑步速度为x千米/小时,步行的速度为y千米/时,则小明跑步3小时后步行2小时,走了(3x+2y)千米;③某小商品以每个3元卖了x个,又以每个2元卖了y个,则共卖了(3x+2y)元.
A.3 B.2 C.1 D.0
【分析】按照代数式的意义和运算顺序判断各项.
【解答】解:“代数式3x+2y”的意义是x的3倍加上y的2倍的和,故①正确;
将“代数式3x+2y”赋予实际意义,可以是小明跑步速度为x千米/小时,步行的速度为y千米/时,则小明跑步3小时后步行2小时,走了(3x+2y)千米,故②正确;
还可以是某小商品以每个3元卖了x个,又以每个2元卖了y个,则共卖了(3x+2y)元,故③正确.
故不正确的有0个.
故选:D.
【点评】此类问题应结合实际,根据代数式的特点解答.注意掌握代数式的意义.
3.买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要( )
A.(4m+7n)元 B.28mn元 C.(7m+4n)元 D.11mn元
【分析】用4个足球的价钱加上7个篮球的价钱即可.
【解答】解:买4个足球、7个篮球共需要(4m+7n)元.
故选:A.
【点评】此题考查列代数式,找出题目蕴含的数量关系是解决问题的关键.
4.元旦,是公历新一年的第一天.“元旦”一词最早出现于《晋书》:“颛帝以孟夏正月为元,其实正朔元旦之春”.中国古代曾以腊月、十月等的月首为元旦.1949年中华人民共和国以公历1月1日为元旦,因此元旦在中国也被称为“阳历年”.为庆祝元旦,人民商场举行促销活动,促销的方法是“消费超过100元时,所购买的商品按原价打8折后,再减少20元”.若某商品的原价为x元(x>100),则购买该商品实际付款的金额(单位:元)是( )
A.80%x﹣20 B.80%(x﹣20) C.20%x﹣20 D.20%(x﹣20)
【分析】根据题意可以用相应的代数式表示购买该商品实际付款的金额.
【解答】解:由题意可得,若某商品的原价为x元(x>100),
则购买该商品实际付款的金额是:80%x﹣20(元),
故选:A.
【点评】本题考查列代数式,解答本题的关键明确题意,列出相应的代数式.
5.在密码学中,直接可以看到内容为明码,对明码进行某种处理后得到的内容为密码、有一种密码,将英文26个字母a,b,c…,z(不论大小写)依次对应1,2,3,…,26这26个自然数.当明码字母对应的序号x为奇数时,密码字母对应的序号是;当明码字母对应的序号x为偶数时,密码字母对应的序号是+14.按上述规定,将明码“hope”译成密码是( )
字母 a b c d e f g h i j k l m
序号 1 2 3 4 5 6 7 8 9 10 11 12 13
字母 n o p q r s t u v w x y z
序号 14 15 16 17 18 19 20 21 22 23 24 25 26
A.gawq B.rivd C.gihe D.hope
【分析】观察可看出,我们需要对所求明码式进行整理然后利用对应代数式代入求得密码序号,再确定其对应字母求解.
【解答】解:根据题意,得h对应的序号是8,则密码对应的序号应是18,即r;
o对应的序号是15,即密码对应的序号是9,即i;
p对应的序号是16,即密码对应的序号是22,即v;
e对应的序号是5,即密码对应的序号是4,即d.
故选:B.
【点评】能够首先说出明码字母对应的序号,再根据定义计算密码对应的序号,进一步确定其对应的字母.
6.小邢到单位附近的加油站加油,如图是小邢所用的加油机上的数据显示牌,则数据中的变量是( )
A.金额 B.数量 C.单价 D.金额和数量
【分析】根据常量与变量的定义即可判断.
【解答】解:常量是固定不变的量,变量是变化的量,
单价是不变的量,而金额是随着数量的变化而变化,
故选:D.
【点评】本题考查常量与变量,解题的关键是正确理解常量与变量,本题属于基础题型.
7.下列关系式中,不是函数关系的是( )
A.y=(x<0) B.y=±(x>0) C.y=(x>0) D.y=﹣(x>0)
【分析】在运动变化过程中,有两个变量x和y,对于x的每一个值y都有唯一确定的值与之对应,那么y是x的函数,x是自变量.
【解答】解:A当x<0时,对于x的每一个值,y=都有唯一确定的值,所以y=(x<0)是函数.
B当x>0时,对于x的每一个值,y=±有两个互为相反数的值,而不是唯一确定的值,所以y=±(x>0)不是函数.
C当x>0时,对于x的每一个值,y=都有唯一确定的值,所以y=(x>0)是函数.
D当x>0时,对于x的每一个值,y=﹣都有唯一确定的值,所以y=﹣(x>0)是函数.
故选:B.
【点评】准确理解函数的概念,用函数的概念作出正确的判断.
8.汽车离开甲站10千米后,以60千米/时的速度匀速前进了t小时,则汽车离开甲站所走的路程s(千米)与时间t(小时)之间的关系式是( )
A.s=10+60t B.s=60t C.s=60t﹣10 D.s=10﹣60t
【分析】根据路程与时间的关系,可得函数解析式.
【解答】解:s=10+60t,
故选:A.
【点评】本题考查了函数关系式,注意先行驶了10千米,路程等于先行驶的加上匀速行驶.
9.函数y=的自变量x的取值范围是( )
A.x>1 B.x<1 C.x≤1 D.x≥1
【分析】根据二次根式的意义,被开方数是非负数.
【解答】解:根据题意得x﹣1≥0,
解得x≥1.
故选:D.
【点评】本题考查了函数自变量的取值范围的确定和分式的意义.函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负数.
10.某地海拔高度h与温度T的关系可用T=21﹣6h来表示(其中温度单位℃,海拔高度单位为千米),则该地区某海拔高度为2000米的山顶上的温度为( )
A.15℃ B.9℃ C.3℃ D.7℃
【分析】把h=2000米=2千米代入T=21﹣6h即得.
【解答】解:2000米=2千米,
T=21﹣6h=21﹣6×2=9℃.
故选:B.
【点评】本题考查函数值的知识,根据题目的信息代入运算即可.
二.填空题(共8小题)
11.代数式6a2的实际意义: 棱长为a的正方体的表面积 .
【分析】从正方体的表面积考虑求解.
【解答】解:代数式6a2表示的实际意义:棱长为a的正方体的表面积.
故答案为:棱长为a的正方体的表面积.
【点评】本题考查代数式的意义问题,对式子进行分析,弄清各项间的关系即可.
12.一台电脑原价a元,降低m元后,又降价20%,现售价为 0.8(a﹣m) 元.
【分析】先表示出降价m元的,然后表示出降价20%的即可.
【解答】解:a元降价m元为(a﹣m)元,
降价20%后为(a﹣m)(1﹣20%)=0.8(a﹣m),
故答案为:0.8(a﹣m).
【点评】本题考查了列代数式的知识,解题的关键是表示出分别表示出两次降价的量,难度不大.
13.如果代数式﹣2a2+3b+8的值为1,那么代数式4a2﹣6b+2的值等于 16 .
【分析】根据﹣2a2+3b+8的值为1,可得:﹣2a2+3b+8=1,所以﹣2a2+3b=﹣7,据此求出代数式4a2﹣6b+2的值等于多少即可.
【解答】解:∵﹣2a2+3b+8的值为1,
∴﹣2a2+3b+8=1,
∴﹣2a2+3b=﹣7,
∴4a2﹣6b+2
=﹣2(﹣2a2+3b)+2
=﹣2×(﹣7)+2
=14+2
=16
故答案为:16.
【点评】此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.
14.已知整数a1,a2,a3,a4,…满足下列条件:a1=0,a2=﹣|a1+1|,a3=﹣|a2+2|,a4=﹣|a3+3|,…,依此类推,则a2019的值为 ﹣1009 .
【分析】根据条件求出前几个数的值,再分n是奇数时,结果等于﹣(n﹣1),n是偶数时,结果等于﹣,然后把n的值代入进行计算即可得解.
【解答】解:a1=0,
a2=﹣|a1+1|=﹣|0+1|=﹣1,
a3=﹣|a2+2|=﹣|﹣1+2|=﹣1,
a4=﹣|a3+3|=﹣|﹣1+3|=﹣2,
a5=﹣|a4+4|=﹣|﹣2+4|=﹣2,
a6=﹣|a5+5|=﹣|﹣2+5|=﹣3,
a7=﹣|a6+6|=﹣|﹣3+6|=﹣3,
…,
所以,n是奇数时,an=﹣(n﹣1),n是偶数时,an=﹣,
∴a2019=﹣(2019﹣1)=﹣1009.
故答案为:﹣1009.
【点评】此题主要考查了数字变化规律,根据所求出的数,观察出n为奇数与偶数时的结果的变化规律是解题的关键.
15.“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中, 温度 随 时间 变化而变化,其中自变量是 时间 ,因变量是 温度 .
【分析】根据函数的定义:对于函数中的每个值x,变量y按照一定的法则有一个确定的值y与之对应;来解答即可.
【解答】解:“早穿皮袄,午穿纱,围着火炉吃西瓜.”这句谚语反映了我国新疆地区一天中,温度随时间变化而变化,其中自变量是:时间,因变量是:温度.
故答案是:温度、时间、时间、温度.
【点评】函数的定义:设x和y是两个变量,D是实数集的某个子集,若对于D中的每个值x,变量y按照一定的法则有一个确定的值y与之对应,称变量y为变量x的函数,记作y=f(x);变量是指在程序的运行过程中随时可以发生变化的量.
16.如图,在△ABC中,∠C=90°,AC=8,BC=6,D点在AC上运动,设AD长为x,△BCD的面积y,则y与x之间的函数表达式为 y=24﹣3x .
【分析】根据三角形的面积=×底×高,结合BC=6,CD=(8﹣x),即可得到,△BCD的面积y与AD的长之间的函数表达式.
【解答】解:根据题意得:
CD的长为:8﹣x,
则y=×6(8﹣x)=24﹣3x,
即y与x之间的函数表达式为:y=24﹣3x.
【点评】本题考查了函数关系式,正确掌握三角形的面积公式是解题的关键.
17.函数y=中,自变量x的取值范围是 x≥2 .
【分析】根据二次根式的性质,被开方数大于等于0,就可以求解.
【解答】解:依题意,得x﹣2≥0,
解得:x≥2,
故答案为:x≥2.
【点评】本题主要考查函数自变量的取值范围,考查的知识点为:二次根式的被开方数是非负数.
18.已知变量y与x的关系式是,则当x=2时,y= ﹣4 .
【分析】将x=2代入y与x的关系式中求解即可.
【解答】解:将x=2代入,
可得:y=3×2﹣×4=6﹣10=﹣4.
故答案为:﹣4.
【点评】本题考查了函数值的知识,当已知函数解析式时,求函数值就是求代数式的值.
三.解答题(共8小题)
19.请将下列代数式进行分类(至少三种以上)
,a,3x,,,,a2+x,4x2ay,x+8.
【分析】根据代数式的分类解答:.
【解答】解:本题答案不唯一.
单项式:,a,3x,4x2ay;
多项式:,a2+x,x+8;
整式:,a,3x,4x2ay,,a2+x,x+8;
分式:.
【点评】本题考查了代数式的定义及其分类.由数和表示数的字母经有限次加、减、乘、除、乘方和开方等代数运算所得的式子,或含有字母的数学表达式称为代数式.注意,分式和无理式都不属于整式.
20.小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含m,n的代数式表示地面的总面积S;
(2)已知n=1.5,且客厅面积是卫生间面积的8倍,如果铺1平方米地砖的平均费用为100元,那么小王铺地砖的总费用为多少元?
【分析】(1)根据总面积等于四个部分矩形的面积之和列式整理即可得解;
(2)根据题意求出m的值,把m,n的值代入计算即可.
【解答】解:(1)S=2n+6m+3×4+2×3=6m+2n+18.
(2)n=1.5时2n=3
根据题意,得6m=8×3=24,
∵铺1平方米地砖的平均费用为100元,
∴铺地砖的总费用为:
100(6m+2n+18)=100×(24+3+18)=4500.
答:铺地砖的总费用4500元.
【点评】此题考查了列代数式,准确表示出各部分矩形的长和宽是解题的关键.
21.某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动.活动期间向客户提供两种优惠方案.
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x条(x>20).
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法和所需费用.
【分析】(1)根据题目提供的两种不同的付款方式列出代数式即可;
(2)将x=30分别代入求得的代数式中即可得到方案一和二的费用,然后比较即可得到选择哪种方案更合算;
(3)根据题意考虑可以先按方案一购买20套西装获赠送20条领带,再按方案二购买10条领带更合算.
【解答】解:(1)方案一购买,需付款:20×200+40(x﹣20)=40x+3200(元),
按方案二购买,需付款:0.9(20×200+40x)=3600+36x(元);
(2)把x=30分别代入:40x+3200=4×30+3200=4400(元),
3600+36×30=4680(元).
因为4400<4680,所以按方案一购买更合算;
(3)先按方案一购买20套西装(送20条领带),再按方案二购买(x﹣20)条领带,共需费用:
20×200+0.9×40(x﹣20)=36x+3280,
当x=30时,36×30+3280=4360(元).
【点评】本题考查了列代数式和求代数式的值的相关的题目,解题的关键是认真分析题目并正确的列出代数式.
22.一种树苗的高度与生长年数之间的关系如下表所示(树高原高100cm)
(1)填出第四年树苗可能达到的高度;
(2)请用含x的代数式表示高度h;
(3)用你得到的代数式求生长了8年后的树苗可能达到的高度
【分析】(1)通过对表格中的数据分析,可知从第二年开始,树苗高度每年增加25cm.因此,第四年树苗高度是在第一年的基础上加3个25.
(2)根据规律可推出第x年树苗的高度h=125+25×(x﹣1);
(3)将数字8代入上面代数式计算即可.
【解答】解:(1)依题意有:第1年是125cm;
第2年是150=(125+25×1)cm;
第3年是175=(125+25×2)cm;
第4年是125+25×3=200cm.
(2)根据规律可得:第x年树苗的高度h=125+25×(x﹣1)=25x+100;所以h=25x+100.
(3)第8年后树苗可能达到的高度为:25×8+100=300cm.
【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键是从第二年开始,逐年增加25cm.
23.希望中学学生从2014年12月份开始每周喝营养牛奶,单价为2元/盒,总价y元随营养牛奶盒数x变化.指出其中的常量与变量,自变量与函数,并写出表示函数与自变量关系的式子.
【分析】根据总价=单价×数量,可得函数关系式.
【解答】解:由题意得:
y=2x,
常量是2,变量是x、y,
x是自变量,y是x的函数.
【点评】主要考查了常量与变量.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
24.阅读下面材料,再回答问题.
一般地,如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=f(x).那么y=f(x)就叫偶函数.如果函数y=f(x)对于自变量取值范围内的任意x,都有f(﹣x)=﹣f(x).那么y=f(x)就叫奇函数.
例如:f(x)=x4
当x取任意实数时,f(﹣x)=(﹣x)4=x4∴f(﹣x)=f(x)∴f(x)=x4是偶函数.
又如:f(x)=2x3﹣x.
当x取任意实数时,∵f(﹣x)=2(﹣x)3﹣(﹣x)=﹣2x3+x=﹣(2x3﹣x)∴f(﹣x)=﹣f(x)∴f(x)=2x3﹣x是奇函数.
问题1:下列函数中:①y=x2+1②③④⑤y=x﹣2﹣2|x|
是奇函数的有 ②④ ;是偶函数的有 ①⑤ (填序号)
问题2:仿照例证明:函数④或⑤是奇函数还是偶函数(选择其中之一)
【分析】(1)根据题目信息,求出f(﹣x)的值,如果f(﹣x)=f(x),则是偶函数,如果f(﹣x)=﹣f(x),则是奇函数;
(2)同(1)的思路进行计算即可证明.
【解答】解:问题1:①y=(﹣x)2+1=x2+1,
∴①是偶函数;
②y==﹣,
∴②是奇函数;
③y=≠≠﹣,
∴③既不是奇函数,也不是偶函数;
④y=﹣x+=﹣(x+),
∴④是奇函数;
⑤y=(﹣x)﹣2﹣2|﹣x|=x﹣2﹣2|x|,
∴⑤是偶函数,
故答案为:奇函数有②④;偶函数有①⑤;
问题2:证明:④∵当x≠0时,
f(﹣x)=﹣x+=﹣(x+)=﹣f(x),
∴y=x+是奇函数,
⑤∵f(﹣x)=(﹣x)﹣2﹣2|﹣x|=x﹣2﹣2|x|=f(x),
∴y=x﹣2﹣2|x|是偶函数.
【点评】本题考查了奇函数与偶函数的定义,根据题目提供信息,看懂题意准确找出题目的解题思路是解题的关键.
25.“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).
(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油量Q(升)的关系式;
(2)当x=280(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
【分析】(1)根据平均每千米的耗油量=总耗油量÷行驶路程即可得出该车平均每千米的耗油量,再根据剩余油量=总油量﹣平均每千米的耗油量×行驶路程即可得出Q关于x的函数关系式;
(2)代入x=280求出Q值即可;
(3)根据行驶的路程=耗油量÷平均每千米的耗油量即可求出报警前能行驶的路程,与景点的往返路程比较后即可得出结论.
【解答】解:(1)该车平均每千米的耗油量为(45﹣30)÷150=0.1(升/千米),
行驶路程x(千米)与剩余油量Q(升)的关系式为Q=45﹣0.1x;
(2)当x=280时,Q=45﹣0.1×280=17(L).
答:当x=280(千米)时,剩余油量Q的值为17L.
(3)(45﹣3)÷0.1=420(千米),
∵420>400,
∴他们能在汽车报警前回到家.
【点评】本题考查了函数的关系式以及一次函数图象上点的坐标特征,根据数量关系列出函数关系式是解题的关键.
26.根据下面的运算程序,若输入时,请计算输出的结果y的值.
【分析】先判断出﹣1的范围,然后根据分段函数解析式,代入相应的解析式进行计算即可求解.
【解答】解:∵0<﹣1<1,
∴输入x=﹣1,
可得y=x2+2x+1=(x+1)2=(﹣1+1)2=2.
故答案为:2.
【点评】本题考查了求函数值,根据x的大小确定出进行计算的函数解析式是解题的关键.
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
