13.5 平行线的性质(2) 导学案(无答案)
文档属性
| 名称 | 13.5 平行线的性质(2) 导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 792.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览

文档简介
课题:13.4平行线的判定(2)
学习目标
1.掌握平行线判定方法2:内错角相等两直线平行.
2.掌握平行线判定方法3:同旁内角互补两直线平行.
学习重点及难点
平行线的判定方法2、判定方法3的推理过程;
学习过程:
一、课前预习:(阅读课本54-55,并思考下列问题)
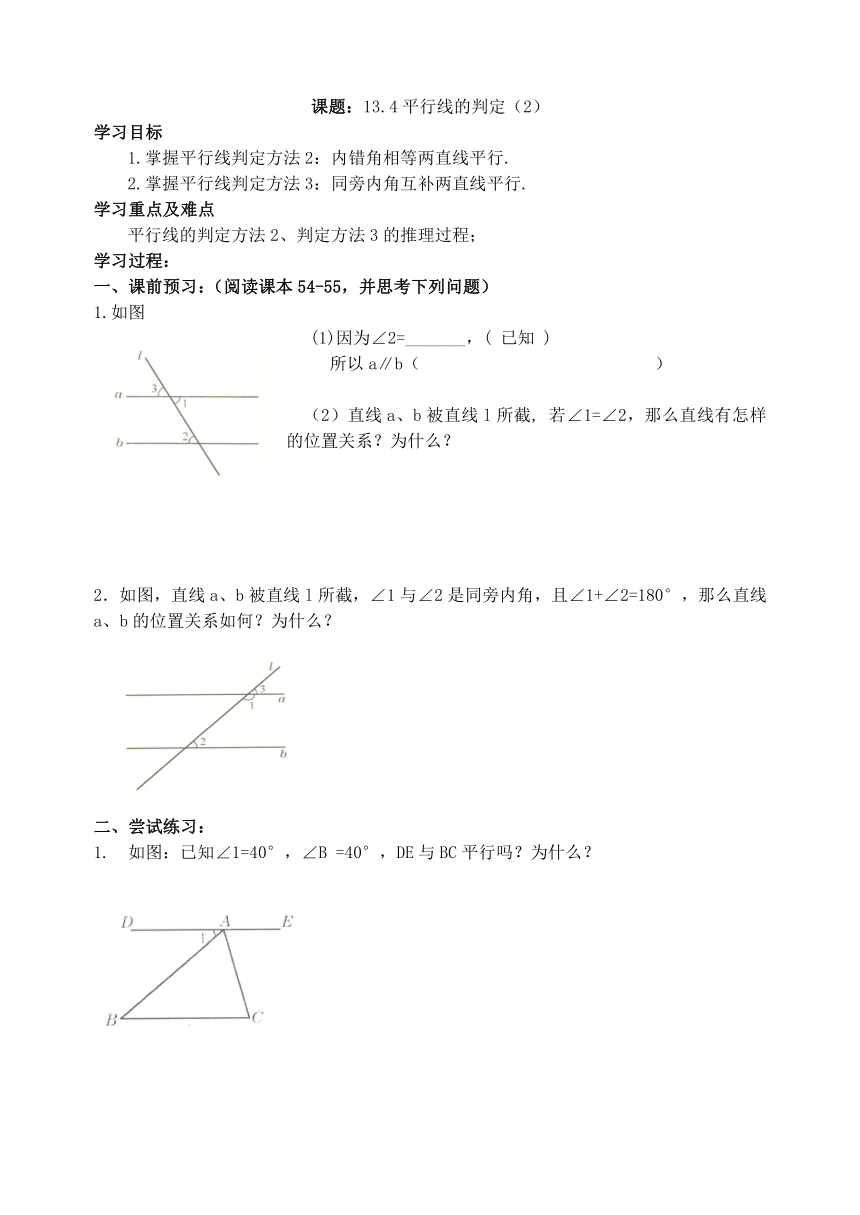
1.如图
(1)因为∠2=_______,( 已知 )
所以a∥b( )
(2)直线a、b被直线l所截, 若∠1=∠2,那么直线有怎样的位置关系?为什么?
2.如图,直线a、b被直线l所截,∠1与∠2是同旁内角,且∠1+∠2=180°,那么直线a、b的位置关系如何?为什么?
二、尝试练习:
1. 如图:已知∠1=40°,∠B =40°,DE与BC平行吗?为什么?
2.如图直线a、b被直线c所截, 已知∠1=60°,∠2 =120°,直线a与b平行吗?为什么?
三、反馈练习:
1.如图1,因为∠B=∠3,所以_______∥______( )
因为∠A=∠2,所以_______∥_______( )
因为∠1=_______,所以AC∥ED( )
因为∠2=________,所以AC∥ED( )
因为∠B+∠BCE=1800,所以______∥____( )
2.如图2,:
(1)∵∠1 =∠4(已知)
∴____∥____(理由_______________________)
(2)∵∠___= ∠___(已知)
∴BC ∥ EF(理由_______________________)
(3) ∵∠1= ∠___(已知)
∴DE ∥____(理由_______________________)
3.如图,过点C有直线MN,AB‖MN的条件是( )
(A)∠B =∠MCA (B)∠A=∠NCB (C)∠A+∠NCB=180 (D)∠MCB+∠B=180
学习目标
1.掌握平行线判定方法2:内错角相等两直线平行.
2.掌握平行线判定方法3:同旁内角互补两直线平行.
学习重点及难点
平行线的判定方法2、判定方法3的推理过程;
学习过程:
一、课前预习:(阅读课本54-55,并思考下列问题)
1.如图
(1)因为∠2=_______,( 已知 )
所以a∥b( )
(2)直线a、b被直线l所截, 若∠1=∠2,那么直线有怎样的位置关系?为什么?
2.如图,直线a、b被直线l所截,∠1与∠2是同旁内角,且∠1+∠2=180°,那么直线a、b的位置关系如何?为什么?
二、尝试练习:
1. 如图:已知∠1=40°,∠B =40°,DE与BC平行吗?为什么?
2.如图直线a、b被直线c所截, 已知∠1=60°,∠2 =120°,直线a与b平行吗?为什么?
三、反馈练习:
1.如图1,因为∠B=∠3,所以_______∥______( )
因为∠A=∠2,所以_______∥_______( )
因为∠1=_______,所以AC∥ED( )
因为∠2=________,所以AC∥ED( )
因为∠B+∠BCE=1800,所以______∥____( )
2.如图2,:
(1)∵∠1 =∠4(已知)
∴____∥____(理由_______________________)
(2)∵∠___= ∠___(已知)
∴BC ∥ EF(理由_______________________)
(3) ∵∠1= ∠___(已知)
∴DE ∥____(理由_______________________)
3.如图,过点C有直线MN,AB‖MN的条件是( )
(A)∠B =∠MCA (B)∠A=∠NCB (C)∠A+∠NCB=180 (D)∠MCB+∠B=180
