13.5 平行线的性质(2)课件(10张PPT)
文档属性
| 名称 | 13.5 平行线的性质(2)课件(10张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 249.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 08:40:47 | ||
图片预览




文档简介
课件10张PPT。13.5平行线的性质(2)由角的大小关系转化为直线的位置关系平行线的判定:口答l 如图所示,直线a,b被直线l所截,
(1)在所得的八个角中,请添加一个条件,使得a∥b;
(2)在三条直线中,请添加一个条件,使得∠1=∠5。平行线的性质:由直线的位置关系转化为角的大小关系 两直线平行,同位角相等,则一对内错角的大小之间有什么关系?一对同旁内角的大小之间有什么关系? (1)已知a//b,任意画一条直线去截平行线。
(2)从中任选一对内错角,进行观察,测量。
(3)从中任选一组同旁内角,进行观察,测量。操作研究思考如图:直线a、b被直线l所截,a∥b,问∠1与∠2有何关系? ∵a∥b(已知),∴∠3=∠2(两直线平行,同位角相等). ∵∠1=∠3(对顶角相等), ∴∠1=∠2(等量代换). 平行线的性质2: 两条平行线被第三条直线所截,内错角相等. 简单地说:就是两直线平行,内错角相等.∴∠1=∠2(两直线平行,内错角相等)∵a∥b(已知)符号语言:∠1的对顶角记作∠3推导
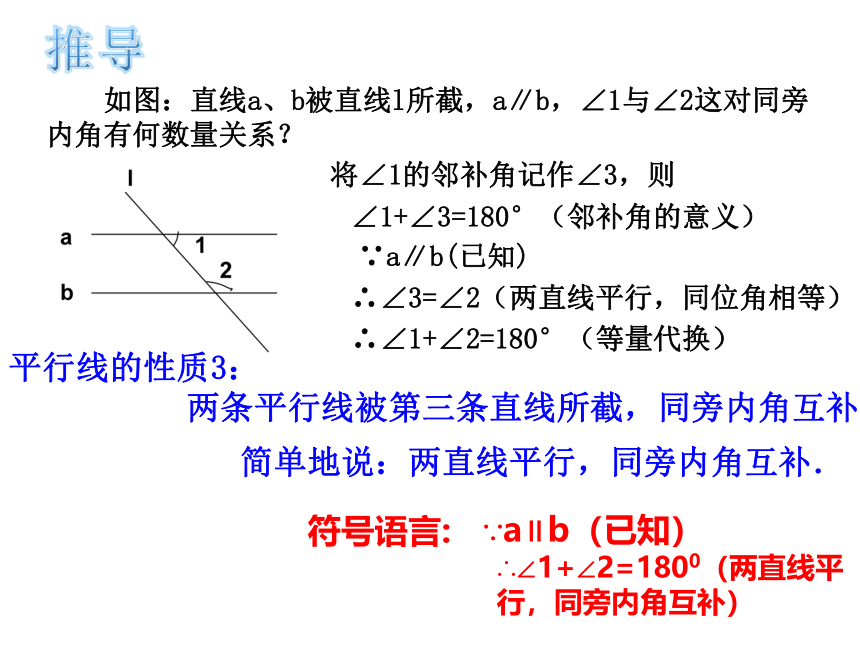
如图:直线a、b被直线l所截,a∥b,∠1与∠2这对同旁内角有何数量关系?将∠1的邻补角记作∠3,则∠1+∠3=180°(邻补角的意义)∵a∥b(已知)∴∠3=∠2(两直线平行,同位角相等) ∴∠1+∠2=180°(等量代换) 平行线的性质3: 两条平行线被第三条直线所截,同旁内角互补. 简单地说:两直线平行,同旁内角互补.∴∠1+∠2=1800(两直线平行,同旁内角互补)∵a∥b(已知)符号语言:推导ADCB
例3 如图,已知AB∥CD,AD∥BC,那么∠1与∠2相等吗?∠3与∠4呢?解 :∵AD∥CB(已知),∴∠1=∠2(两直线平行,内错角相等).∵AB∥CD(已知),∴∠3=∠4(两直线平行,内错角相等) 例题分析
例4 如图,已知AB∥CD,AD∥BC,∠A=55°, 求∠B,∠C,∠D的度数.
如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110°,可以知道∠2 是多少度?为什么?
(2)从∠1=110°,可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110°,可以知道∠4 是多少度?为什么?
2∠4=70o
∵两直线平行,同旁内角互补巩固练习“平行线的判定”与“平行线的性质”判定性质同位角相等,两直线平行。内错角相等,两直线平行。同旁内角互补,两直线平行。两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.课堂小结练习册:13.5(2) 作业布置
(1)在所得的八个角中,请添加一个条件,使得a∥b;
(2)在三条直线中,请添加一个条件,使得∠1=∠5。平行线的性质:由直线的位置关系转化为角的大小关系 两直线平行,同位角相等,则一对内错角的大小之间有什么关系?一对同旁内角的大小之间有什么关系? (1)已知a//b,任意画一条直线去截平行线。
(2)从中任选一对内错角,进行观察,测量。
(3)从中任选一组同旁内角,进行观察,测量。操作研究思考如图:直线a、b被直线l所截,a∥b,问∠1与∠2有何关系? ∵a∥b(已知),∴∠3=∠2(两直线平行,同位角相等). ∵∠1=∠3(对顶角相等), ∴∠1=∠2(等量代换). 平行线的性质2: 两条平行线被第三条直线所截,内错角相等. 简单地说:就是两直线平行,内错角相等.∴∠1=∠2(两直线平行,内错角相等)∵a∥b(已知)符号语言:∠1的对顶角记作∠3推导
如图:直线a、b被直线l所截,a∥b,∠1与∠2这对同旁内角有何数量关系?将∠1的邻补角记作∠3,则∠1+∠3=180°(邻补角的意义)∵a∥b(已知)∴∠3=∠2(两直线平行,同位角相等) ∴∠1+∠2=180°(等量代换) 平行线的性质3: 两条平行线被第三条直线所截,同旁内角互补. 简单地说:两直线平行,同旁内角互补.∴∠1+∠2=1800(两直线平行,同旁内角互补)∵a∥b(已知)符号语言:推导ADCB
例3 如图,已知AB∥CD,AD∥BC,那么∠1与∠2相等吗?∠3与∠4呢?解 :∵AD∥CB(已知),∴∠1=∠2(两直线平行,内错角相等).∵AB∥CD(已知),∴∠3=∠4(两直线平行,内错角相等) 例题分析
例4 如图,已知AB∥CD,AD∥BC,∠A=55°, 求∠B,∠C,∠D的度数.
如图,已知平行线AB、CD被直线AE所截
(1)从 ∠1=110°,可以知道∠2 是多少度?为什么?
(2)从∠1=110°,可以知道 ∠3是多少度?为什么?
(3)从 ∠1=110°,可以知道∠4 是多少度?为什么?
2∠4=70o
∵两直线平行,同旁内角互补巩固练习“平行线的判定”与“平行线的性质”判定性质同位角相等,两直线平行。内错角相等,两直线平行。同旁内角互补,两直线平行。两直线平行,同位角相等.两直线平行,内错角相等.两直线平行,同旁内角互补.课堂小结练习册:13.5(2) 作业布置
