12.1 实数的概念 课件(19张PPT)
文档属性
| 名称 | 12.1 实数的概念 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 436.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 14:21:21 | ||
图片预览






文档简介
课件19张PPT。12. 1 实数的概念1、体验发现无理数的过程,知道什么是无理数。
2、会区分有理数和无理数。
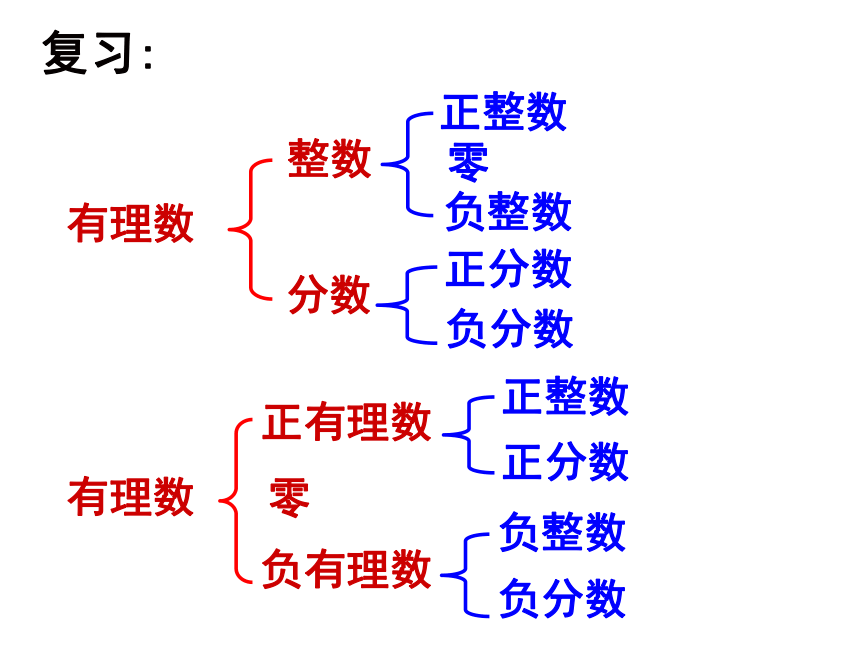
3、了解数的范围,从整数→有理数→实数的扩展过程,知道实数的意义及分类学习目标:复习:有理数整数分数正整数 零负整数正分数负分数有理数正有理数零负有理数正整数正分数负整数负分数 有理数中的分数能化为小数的,那么化为什么样的小数呢?我们举例来说明。 答:任何一个分数可写成小数的形式,
必是有限小数或者无限循环小数。 例如无限不循环小数叫做无理数。1、开不尽方的数都是无理数注意:带根号的数不一定是无理数例如:你知道哪些数是无理数?结果显示为:1.414 213 562问题2:你能利用平方关系验算得到的结果吗?
问题1 中的结果平方后会等于2吗?做一做 用计算器计算:1.414 213 5622
=1.999 999 999问题2:验证的结果不是2,而是接近2, 这说明什么?做一做 1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605715……问题4:后面能否写完?后面有没有规律? 那么它属于什么小数?例如:2、圆周率 及一些含有 的式子都是无理数3、有一定的规律,但不循环的无限小数都是无理数。例如:
0.1010010001…〔两个1之间依次多1个0〕
—168.3232232223…〔两个3之间依次多1个2〕0.12345678910111213 …〔小数部分有相继的正整数组成〕
有限小数无限循环小数无理数无限不循环小数实数实数的分类1、无限不循环小数叫做无理数
如: 等。2、有理数与无理数统称为实数。无理数也像有理数一样广泛存在着。
无理数也有正负之分,例如正无理数:
负无理数:
正有理数 整数 正有理数
正数 有理数 或 零
正无理数 分数 负有理数
零 或
负有理数 正无理数
负数 无理数
负无理数 负无理数实数的分类实数实数把下列各数分别填入相应的圆圈内:练习与小结一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.无理数都是开方开不尽的数。( )7. 无理数包括正无理数、零、负无理数。( )×××8.有理数都是有限小数。( )××2、把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)负数集合:(5)分数集合:(6)实数集合:小结:1.判断一个数是不是无理数,必须看它是否同时满足两个条件:无限小数和不循环小数这两者缺一不可. 2.带根号的数并不都是无理数,而开方开不尽的数才是无理数. 3.掌握实数的不同分类法.
正有理数 整数 正有理数
正数 有理数 或 零
正无理数 分数 负有理数
零 或
负有理数 正无理数
负数 无理数
负无理数 负无理数实数的分类实数实数
2、会区分有理数和无理数。
3、了解数的范围,从整数→有理数→实数的扩展过程,知道实数的意义及分类学习目标:复习:有理数整数分数正整数 零负整数正分数负分数有理数正有理数零负有理数正整数正分数负整数负分数 有理数中的分数能化为小数的,那么化为什么样的小数呢?我们举例来说明。 答:任何一个分数可写成小数的形式,
必是有限小数或者无限循环小数。 例如无限不循环小数叫做无理数。1、开不尽方的数都是无理数注意:带根号的数不一定是无理数例如:你知道哪些数是无理数?结果显示为:1.414 213 562问题2:你能利用平方关系验算得到的结果吗?
问题1 中的结果平方后会等于2吗?做一做 用计算器计算:1.414 213 5622
=1.999 999 999问题2:验证的结果不是2,而是接近2, 这说明什么?做一做 1.4142135623730950488016887242096980785696718753769480731766797379907324784621070388503875343276415727350138462309122970249248360558507372126441214970999358314132226659275055927557999505011527820605715……问题4:后面能否写完?后面有没有规律? 那么它属于什么小数?例如:2、圆周率 及一些含有 的式子都是无理数3、有一定的规律,但不循环的无限小数都是无理数。例如:
0.1010010001…〔两个1之间依次多1个0〕
—168.3232232223…〔两个3之间依次多1个2〕0.12345678910111213 …〔小数部分有相继的正整数组成〕
有限小数无限循环小数无理数无限不循环小数实数实数的分类1、无限不循环小数叫做无理数
如: 等。2、有理数与无理数统称为实数。无理数也像有理数一样广泛存在着。
无理数也有正负之分,例如正无理数:
负无理数:
正有理数 整数 正有理数
正数 有理数 或 零
正无理数 分数 负有理数
零 或
负有理数 正无理数
负数 无理数
负无理数 负无理数实数的分类实数实数把下列各数分别填入相应的圆圈内:练习与小结一、判断:1.实数不是有理数就是无理数。( )2.无理数都是无限不循环小数。( )3.无理数都是无限小数。( )4.带根号的数都是无理数。( )5.无理数一定都带根号。( )6.无理数都是开方开不尽的数。( )7. 无理数包括正无理数、零、负无理数。( )×××8.有理数都是有限小数。( )××2、把下列各数填入相应的集合内:(1)有理数集合:(2)无理数集合:(3)整数集合:(4)负数集合:(5)分数集合:(6)实数集合:小结:1.判断一个数是不是无理数,必须看它是否同时满足两个条件:无限小数和不循环小数这两者缺一不可. 2.带根号的数并不都是无理数,而开方开不尽的数才是无理数. 3.掌握实数的不同分类法.
正有理数 整数 正有理数
正数 有理数 或 零
正无理数 分数 负有理数
零 或
负有理数 正无理数
负数 无理数
负无理数 负无理数实数的分类实数实数
