12.1 实数的概念 课件(10张PPT)
文档属性
| 名称 | 12.1 实数的概念 课件(10张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 150.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览


文档简介
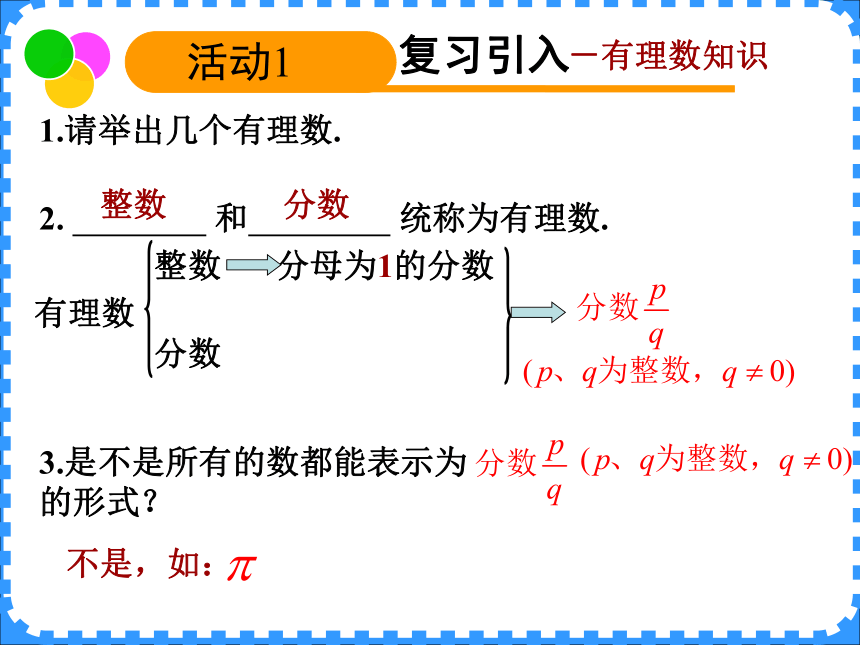
课件10张PPT。12.1实数的概念七年级下册第十二章实数1.请举出几个有理数. 复习引入活动1 2. 和 统称为有理数. 分数整数分数分母为1的分数3.是不是所有的数都能表示为
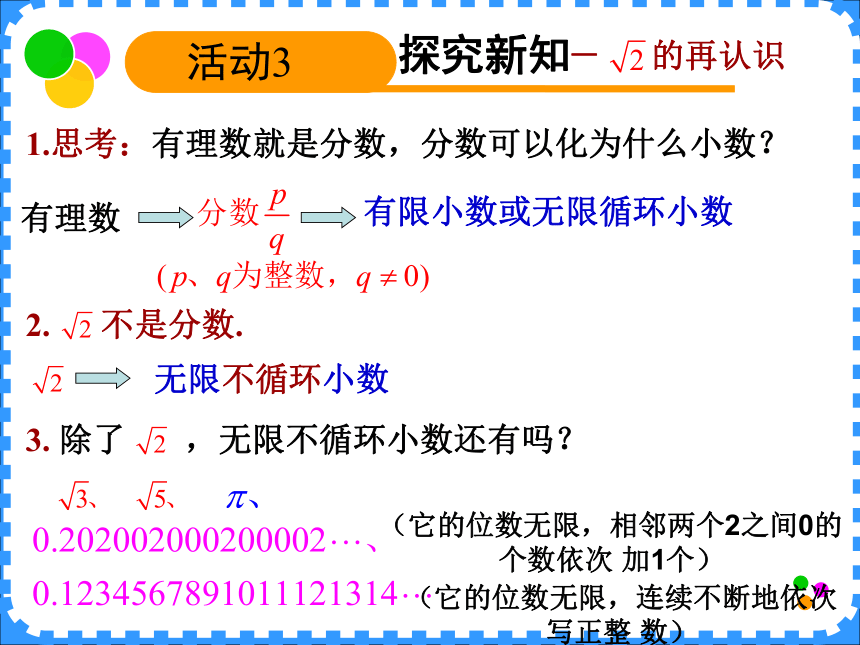
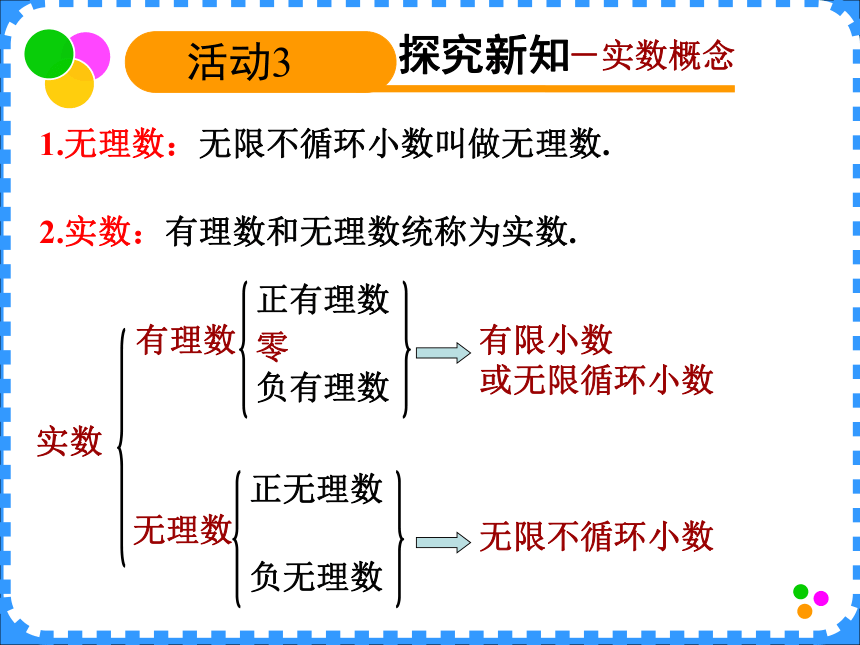
的形式?不是,如:-有理数知识 有理数整数探究新知活动2 思考1:能否将两个边长为1的正方形剪拼成一个大正方形?怎样剪拼?它的面积是多少?边长如何表示?设该正方形的边长为x,那么 .这时将边长用 来表示; 读作“根号2”.思考2:面积为3的正方形,它的边长又如何表示?若面积为5呢?,读作“根号3”,读作“根号5”-操作剪拼 另一种剪拼方法探究新知活动3 - 的再认识 1.思考:有理数就是分数,分数可以化为什么小数?有理数有限小数或无限循环小数2. 不是分数.无限不循环小数3. 除了 ,无限不循环小数还有吗?(它的位数无限,相邻两个2之间0的个数依次 加1个)(它的位数无限,连续不断地依次写正整 数)探究新知活动3 1.无理数:无限不循环小数叫做无理数.-实数概念 2.实数:有理数和无理数统称为实数.有限小数
或无限循环小数负有理数正有理数有理数负无理数正无理数无理数无限不循环小数零实数探究新知活动3 例题1 将下列各数放入图中适当的位置:-知识应用 3.14、0、–24 是分数,所以是有理数探究新知活动3 例题2 判断下列说法是否正确,并说明理由. -知识应用 (1) 无限小数都是无理数;( ) (2) 无理数都是无限小数;( )(3) 正实数包括正有理数和正无理数;( )(4) 实数可以分为正实数和负实数两类.( )× × √ √ 无限循环小数和无限不循环小数 无限不循环小数 零既不是正实数,也不是负实数正无理数正有理数正实数负无理数负有理数负实数零实数课堂练习活动4 -及时巩固 (每相邻两个“8”之间的“1”的个数从左到右依次递增且是无限小数)中,
无理数有 ,
正有理数有 ,
非负数有 ,
整数有 .0课堂练习活动4 方法二:由正方形面积构成;-及时巩固 2.请写成几个在3和4之间的无理数.3.课本P5 练习2方法一:由 构成;方法三:按规律生成;…自我小结活动5 -反思建构 1.无理数:无限不循环小数叫做无理数.2.实数:有理数和无理数统称为实数.3.实数的分类.
的形式?不是,如:-有理数知识 有理数整数探究新知活动2 思考1:能否将两个边长为1的正方形剪拼成一个大正方形?怎样剪拼?它的面积是多少?边长如何表示?设该正方形的边长为x,那么 .这时将边长用 来表示; 读作“根号2”.思考2:面积为3的正方形,它的边长又如何表示?若面积为5呢?,读作“根号3”,读作“根号5”-操作剪拼 另一种剪拼方法探究新知活动3 - 的再认识 1.思考:有理数就是分数,分数可以化为什么小数?有理数有限小数或无限循环小数2. 不是分数.无限不循环小数3. 除了 ,无限不循环小数还有吗?(它的位数无限,相邻两个2之间0的个数依次 加1个)(它的位数无限,连续不断地依次写正整 数)探究新知活动3 1.无理数:无限不循环小数叫做无理数.-实数概念 2.实数:有理数和无理数统称为实数.有限小数
或无限循环小数负有理数正有理数有理数负无理数正无理数无理数无限不循环小数零实数探究新知活动3 例题1 将下列各数放入图中适当的位置:-知识应用 3.14、0、–24 是分数,所以是有理数探究新知活动3 例题2 判断下列说法是否正确,并说明理由. -知识应用 (1) 无限小数都是无理数;( ) (2) 无理数都是无限小数;( )(3) 正实数包括正有理数和正无理数;( )(4) 实数可以分为正实数和负实数两类.( )× × √ √ 无限循环小数和无限不循环小数 无限不循环小数 零既不是正实数,也不是负实数正无理数正有理数正实数负无理数负有理数负实数零实数课堂练习活动4 -及时巩固 (每相邻两个“8”之间的“1”的个数从左到右依次递增且是无限小数)中,
无理数有 ,
正有理数有 ,
非负数有 ,
整数有 .0课堂练习活动4 方法二:由正方形面积构成;-及时巩固 2.请写成几个在3和4之间的无理数.3.课本P5 练习2方法一:由 构成;方法三:按规律生成;…自我小结活动5 -反思建构 1.无理数:无限不循环小数叫做无理数.2.实数:有理数和无理数统称为实数.3.实数的分类.
