北师大版八年级数学上册 2.1认识无理数课件(第1课时 共16张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 2.1认识无理数课件(第1课时 共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 925.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 14:10:46 | ||
图片预览




文档简介
(共16张PPT)
1.认识无理数
第二章 实数
兴宁市大坪中学 练小盛
1.理解无理数的概念,会判断一个数是有理数还是无理数.
2.能在数轴上表示某些简单的无理数.
学习目标
整数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
分数
正分数:如 , , 5.2, …
负分数如 , ,-3.5, …
有理数
回顾 & 思考
?
什么叫有理数?
??? 毕达哥拉斯认为世间万物都可以用整数或整数之比来表示,即都可用有理数来描述。你认为这个断言正确吗?
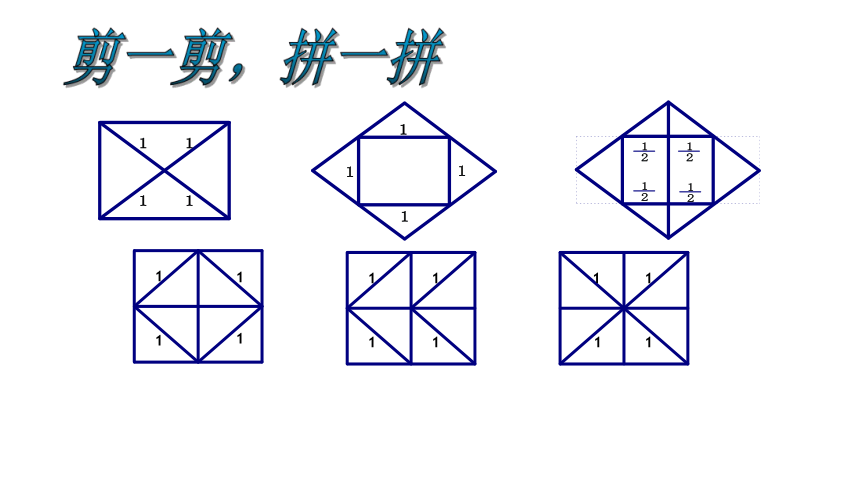
把两个边长为1的小正方形拼成一个大正方形
剪一剪 拼一拼
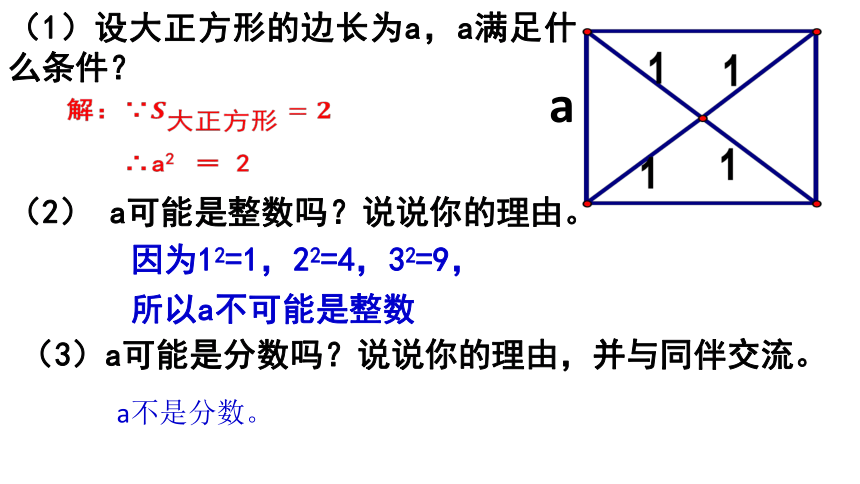
⑴ 设大正方形的边长为a,a满足什么条件?
⑵ a可能是整数吗?说说你的理由。
(3)a可能是分数吗?说说你的理由,并与同伴交流。
活动一 ?
剪一剪,拼一拼
(1)设大正方形的边长为a,a满足什么条件?
(3)a可能是分数吗?说说你的理由,并与同伴交流。
(2) a可能是整数吗?说说你的理由。
因为12=1,22=4,32=9,
所以a不可能是整数
解:∵
∴a2 = 2
a
a不是分数。
结论:在等式a2=2中,a既不是整数,也不是分数,所以a不是有理数。
a究竟是什么数?
a
探索:
它的出现引起数学史上第一次危机
?(1) 如图,以直角三角形的斜边为边的正方形的面积是多少?
?(2) 设该正方形的边长为b,b满足什么条件?
?(3) b是有理数吗?
做一做
活动二 ?
b
解:(1)
(2)∵
∴
(3)b即不是整数也不是分数,b不是有理数.
例题:设面积为6的圆的半径为y。
y是有理数吗?说说你的理由。
1、如图,等边三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?
随堂练习
答:h不可能是整数也不可能是分数。
2、下面各正方形的边长不是有理数的是( )
(A)面积为25的正方形
(B)面积为16的正方形
(C)面积为7的正方形
(D)面积为1.44的正方形
C
3、如图,Rt△ABC的三边分别为a、b、c。
(1)根据所给a、b的值,求出c2的值。
① a=1,b=2, c2 =——,
② a=3,b=4, c2 =——,
③ a=5,b=6, c2 =——,
④ a=0.6,b=0.8, c2 =——,
(2)分析上述c2的结果,我们知道,c是整数的有 ____,c是分数的有______,c既不是整数又不是分数的有__ (填上序号)
5
25
61
1
②__④
①③
4、下图中阴影部分是正方形,求出此正方形的面积。此正方形的边长是有理数吗?为什么?
8
17
a
解:
即
因为所以a不是有理数。
找一找
在下列正方形网格中,先找出长度为有
理数的线段,再找出长度不是有理数的
线段.
小结
本节课从实际背景中发现不可比的数,感受这样的数广泛存在。
作业
1.课本P22面习题2.1 1,2
2.复习前面内容并预习下节内容
1.认识无理数
第二章 实数
兴宁市大坪中学 练小盛
1.理解无理数的概念,会判断一个数是有理数还是无理数.
2.能在数轴上表示某些简单的无理数.
学习目标
整数
正整数:如:1,2,3,…
零:0
负整数:如-1,-2,-3,…
分数
正分数:如 , , 5.2, …
负分数如 , ,-3.5, …
有理数
回顾 & 思考
?
什么叫有理数?
??? 毕达哥拉斯认为世间万物都可以用整数或整数之比来表示,即都可用有理数来描述。你认为这个断言正确吗?
把两个边长为1的小正方形拼成一个大正方形
剪一剪 拼一拼
⑴ 设大正方形的边长为a,a满足什么条件?
⑵ a可能是整数吗?说说你的理由。
(3)a可能是分数吗?说说你的理由,并与同伴交流。
活动一 ?
剪一剪,拼一拼
(1)设大正方形的边长为a,a满足什么条件?
(3)a可能是分数吗?说说你的理由,并与同伴交流。
(2) a可能是整数吗?说说你的理由。
因为12=1,22=4,32=9,
所以a不可能是整数
解:∵
∴a2 = 2
a
a不是分数。
结论:在等式a2=2中,a既不是整数,也不是分数,所以a不是有理数。
a究竟是什么数?
a
探索:
它的出现引起数学史上第一次危机
?(1) 如图,以直角三角形的斜边为边的正方形的面积是多少?
?(2) 设该正方形的边长为b,b满足什么条件?
?(3) b是有理数吗?
做一做
活动二 ?
b
解:(1)
(2)∵
∴
(3)b即不是整数也不是分数,b不是有理数.
例题:设面积为6的圆的半径为y。
y是有理数吗?说说你的理由。
1、如图,等边三角形ABC的边长为2,高为h,h可能是整数吗?可能是分数吗?
随堂练习
答:h不可能是整数也不可能是分数。
2、下面各正方形的边长不是有理数的是( )
(A)面积为25的正方形
(B)面积为16的正方形
(C)面积为7的正方形
(D)面积为1.44的正方形
C
3、如图,Rt△ABC的三边分别为a、b、c。
(1)根据所给a、b的值,求出c2的值。
① a=1,b=2, c2 =——,
② a=3,b=4, c2 =——,
③ a=5,b=6, c2 =——,
④ a=0.6,b=0.8, c2 =——,
(2)分析上述c2的结果,我们知道,c是整数的有 ____,c是分数的有______,c既不是整数又不是分数的有__ (填上序号)
5
25
61
1
②__④
①③
4、下图中阴影部分是正方形,求出此正方形的面积。此正方形的边长是有理数吗?为什么?
8
17
a
解:
即
因为所以a不是有理数。
找一找
在下列正方形网格中,先找出长度为有
理数的线段,再找出长度不是有理数的
线段.
小结
本节课从实际背景中发现不可比的数,感受这样的数广泛存在。
作业
1.课本P22面习题2.1 1,2
2.复习前面内容并预习下节内容
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
