北师大版八年级数学上册 2.4估算课件(共22张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 2.4估算课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-12 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
4 估算
第二章 实数
兴宁市大坪中学 练小盛
北师大八年级数学(上)
400000米2
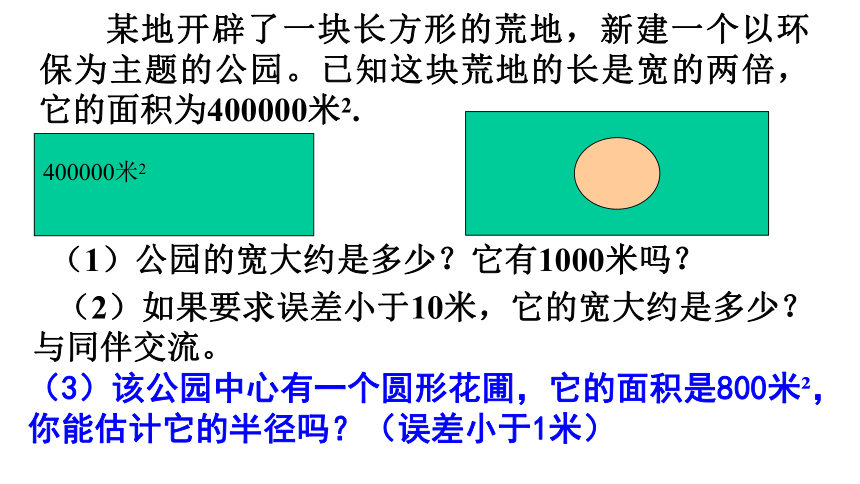
某地开辟了一块长方形的荒地,新建一个以环保为主题的公园。已知这块荒地的长是宽的两倍,它的面积为400000米2.
(1)公园的宽大约是多少?它有1000米吗?
(2)如果要求误差小于10米,它的宽大约是多少?与同伴交流。
(3)该公园中心有一个圆形花圃,它的面积是800米?,你能估计它的半径吗?(误差小于1米)
解:设公园的宽为m,则它的长为2m,依题意得
议一议
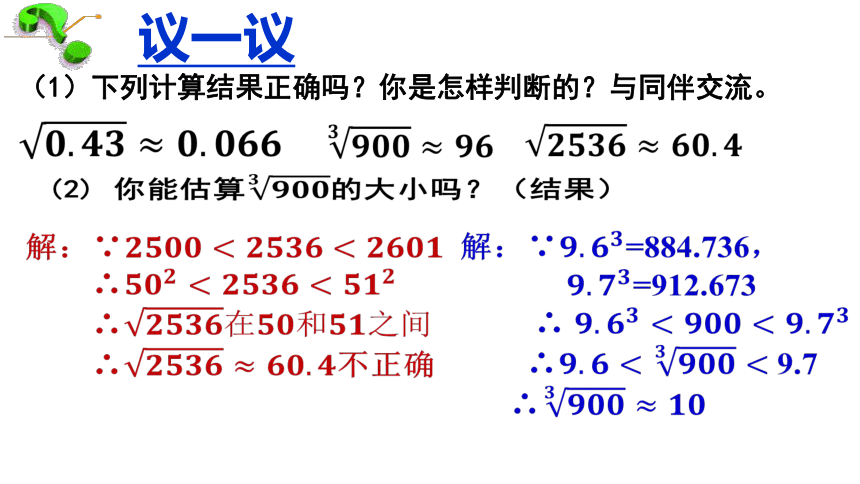
(1)下列计算结果正确吗?你是怎样判断的?与同伴交流。
(2) 你能估算的大小吗?
解:∵
∴
∴
∴不正确
解:∵
∴
∴
∴不正确
议一议
(1)下列计算结果正确吗?你是怎样判断的?与同伴交流。
(2) 你能估算的大小吗?(结果)
解:∵=884.736,
=912.673
∴
∴ 9.7
∴
解:∵
∴
∴
∴不正确
你能估算它们的大小吗?说出你的方法
( ①②误差小于0.1,③误差小于10).
误差小于0.1就是指估算出来的值与准确值之间的差的绝对值小于0.1.
①
②
③
解:
①
②
③
精确到1是计算到十分位四舍五入到个位;
误差小于1是在其值左右1上下都符合题意,答案不唯一。
怎样估算无理数 (误差小于0.1)?
夹逼法
夹逼法:两边无限逼近的方法,估算首先确定其整数部分的范围,再确定十分位,百分位等 小数部分。
估算有一定的精度要求。
1 估算无理数的方法是(1)通过平方运算,采用“夹逼法”,确定真值所在范围;(2)根据问题中误差允许的范围,在真值的范围内取出近似值。
2 “精确到”与“误差小于”意义不同。如精确到1m是四舍五入到个位,答案惟一;误差小于1m,答案在真值左右1m都符合题意,答案不惟一。在本章中误差小于1m就是估算到个位,误差小于10m就是估算到十位。
知识点小结
例1 生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的1/3,则梯子比较稳定。现有一长度为6米的梯子,当梯子稳定摆放时,它的顶端能达到5.6米高的墙头吗?
C
B
A
例1 生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的1/3,则梯子比较稳定。现有一长度为6米的梯子,当梯子稳定摆放时,它的顶端能达到5.6米高的墙头吗?
解:设梯子稳定摆放时的高度为x m,此时梯子底端离墙恰好为梯子长度的,根据题意,得
6
A
B
C
因此,梯子稳定摆放时,它的顶端能够达到5.6m高的墙头
∵
∴
(2)小明是这样想的: 与 的分母相同,
只要比较它们的分子就可以了,
因为 ,所以 ,
因此 ,你认为小明的想法正确吗?
用估算来解决数学问题
(1)你能比较 与 的大小吗?
你怎样想的?与同伴交流.
解:∵
∴1
∴
(2)小明的想法正确。
(2)如果要求误差小于10 m,它的宽大约是?
(大约440 m或450 m,其实
440 m与450 m之间的值都可以)
(3)该公园中心有一个圆形花圃,它的
面积是800你能估计它的半径吗?
(误差小于1米)
(1)公园宽
用估算来解决实际问题
(15 m与16 m之间的值都可以)
随堂练习:
1.估算下列数的大小:
解:
3.6或3.7(实际上只要在3.6和3.7之间的数都可以);
(2) 9或10(实际上只要在9和10之间的数都可以).
(1) (误差小于0.1);(2) (误差小于1)
2.通过估算,比较与2.5的大小
解:∵
又∵6.25
∴
即
3.通过估算,比较下面各组数的大小:
(1) ≈ 9.5
(2) ≈ 231
4.下列结果正确吗?说说你的理由:
5.一个人每天平均要饮用大约0.0015米3的各种液体,按70岁计算,他所饮用的液体总量大约为40米3。如果用一圆柱形的容器(底面直径等于高)来装这些液体,这个容器大约有多高?(误差小于1米)
A
B
C
O
5.一个人每天平均要饮用大约0.0015米3的各种液体,按70岁计算,他所饮用的液体总量大约为40米3。如果用一圆柱形的容器(底面直径等于高)来装这些液体,这个容器大约有多高?(误差小于1 m)
解:设圆柱的高
为 x,那么它的
底面半径为0.5x,
依题意,得
4
答:这个容器大约4米高.
1 估算无理数的方法是(1)通过平方运算,采用“夹逼法”,确定真值所在范围;(2)根据问题中误差允许的范围,在真值的范围内取出近似值。
2 “精确到”与“误差小于”意义不同。如精确到1m是四舍五入到个位,答案惟一;误差小于1m,答案在真值左右1m都符合题意,答案不惟一。在本章中误差小于1m就是估算到个位,误差小于10m就是估算到十位。
知识点小结
作业巩固:课本P34面习题2.6 1,2,3.
估算比较大小的方法:
1,两个带根号的无理数比较,直接比较被开方数
如:a>b≥0则
2,无理数和有理数比较,直接把有理数平方或立方与无理数的被开方数比较 如: 和3即比较 和
3,平方法:如 和 即( )2和( )2
4,作差法:两个被比较的数相减的差来和0比较,差大于0则被减数大;小于0则减数大;等于0则两数同样大。
托尔斯泰是俄罗斯最伟大的作家,他曾在作品《一个人需要很多土地吗?》中写了如下一个故事:有一个叫巴河姆的人到草原上去购买土地,卖地的人提出了一个非常奇怪的地价:“每天1000卢布”,意思是谁出1000卢布,那么他从日出到日落走过的路所围成的土地都归他;不过如果在日落之前,买地的人回不到原来的出发点,那他就只好白出1000卢布。巴河姆于是付了1000卢布,等第二天太阳刚刚从地平线上升起,就连忙在草原上大步向前走去。他走了足足有10俄里(1俄里=1.0668公里),这才朝左拐弯;接着又走了许久许久,才再向左拐弯;这样有走了2俄里,这时他发现天色已经不早,而自己离出发点足足还有15俄里的路程,于是只得改变方向,径直朝出发点跑去……最后,他总算如期赶回出发点,却口吐鲜血死去。请你算一算,他这一天共走了多少路?他走过的路围成的土地有多大?(精确到0.1)
挑战自我
4 估算
第二章 实数
兴宁市大坪中学 练小盛
北师大八年级数学(上)
400000米2
某地开辟了一块长方形的荒地,新建一个以环保为主题的公园。已知这块荒地的长是宽的两倍,它的面积为400000米2.
(1)公园的宽大约是多少?它有1000米吗?
(2)如果要求误差小于10米,它的宽大约是多少?与同伴交流。
(3)该公园中心有一个圆形花圃,它的面积是800米?,你能估计它的半径吗?(误差小于1米)
解:设公园的宽为m,则它的长为2m,依题意得
议一议
(1)下列计算结果正确吗?你是怎样判断的?与同伴交流。
(2) 你能估算的大小吗?
解:∵
∴
∴
∴不正确
解:∵
∴
∴
∴不正确
议一议
(1)下列计算结果正确吗?你是怎样判断的?与同伴交流。
(2) 你能估算的大小吗?(结果)
解:∵=884.736,
=912.673
∴
∴ 9.7
∴
解:∵
∴
∴
∴不正确
你能估算它们的大小吗?说出你的方法
( ①②误差小于0.1,③误差小于10).
误差小于0.1就是指估算出来的值与准确值之间的差的绝对值小于0.1.
①
②
③
解:
①
②
③
精确到1是计算到十分位四舍五入到个位;
误差小于1是在其值左右1上下都符合题意,答案不唯一。
怎样估算无理数 (误差小于0.1)?
夹逼法
夹逼法:两边无限逼近的方法,估算首先确定其整数部分的范围,再确定十分位,百分位等 小数部分。
估算有一定的精度要求。
1 估算无理数的方法是(1)通过平方运算,采用“夹逼法”,确定真值所在范围;(2)根据问题中误差允许的范围,在真值的范围内取出近似值。
2 “精确到”与“误差小于”意义不同。如精确到1m是四舍五入到个位,答案惟一;误差小于1m,答案在真值左右1m都符合题意,答案不惟一。在本章中误差小于1m就是估算到个位,误差小于10m就是估算到十位。
知识点小结
例1 生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的1/3,则梯子比较稳定。现有一长度为6米的梯子,当梯子稳定摆放时,它的顶端能达到5.6米高的墙头吗?
C
B
A
例1 生活经验表明,靠墙摆放梯子时,若梯子底端离墙的距离约为梯子长度的1/3,则梯子比较稳定。现有一长度为6米的梯子,当梯子稳定摆放时,它的顶端能达到5.6米高的墙头吗?
解:设梯子稳定摆放时的高度为x m,此时梯子底端离墙恰好为梯子长度的,根据题意,得
6
A
B
C
因此,梯子稳定摆放时,它的顶端能够达到5.6m高的墙头
∵
∴
(2)小明是这样想的: 与 的分母相同,
只要比较它们的分子就可以了,
因为 ,所以 ,
因此 ,你认为小明的想法正确吗?
用估算来解决数学问题
(1)你能比较 与 的大小吗?
你怎样想的?与同伴交流.
解:∵
∴1
∴
(2)小明的想法正确。
(2)如果要求误差小于10 m,它的宽大约是?
(大约440 m或450 m,其实
440 m与450 m之间的值都可以)
(3)该公园中心有一个圆形花圃,它的
面积是800你能估计它的半径吗?
(误差小于1米)
(1)公园宽
用估算来解决实际问题
(15 m与16 m之间的值都可以)
随堂练习:
1.估算下列数的大小:
解:
3.6或3.7(实际上只要在3.6和3.7之间的数都可以);
(2) 9或10(实际上只要在9和10之间的数都可以).
(1) (误差小于0.1);(2) (误差小于1)
2.通过估算,比较与2.5的大小
解:∵
又∵6.25
∴
即
3.通过估算,比较下面各组数的大小:
(1) ≈ 9.5
(2) ≈ 231
4.下列结果正确吗?说说你的理由:
5.一个人每天平均要饮用大约0.0015米3的各种液体,按70岁计算,他所饮用的液体总量大约为40米3。如果用一圆柱形的容器(底面直径等于高)来装这些液体,这个容器大约有多高?(误差小于1米)
A
B
C
O
5.一个人每天平均要饮用大约0.0015米3的各种液体,按70岁计算,他所饮用的液体总量大约为40米3。如果用一圆柱形的容器(底面直径等于高)来装这些液体,这个容器大约有多高?(误差小于1 m)
解:设圆柱的高
为 x,那么它的
底面半径为0.5x,
依题意,得
4
答:这个容器大约4米高.
1 估算无理数的方法是(1)通过平方运算,采用“夹逼法”,确定真值所在范围;(2)根据问题中误差允许的范围,在真值的范围内取出近似值。
2 “精确到”与“误差小于”意义不同。如精确到1m是四舍五入到个位,答案惟一;误差小于1m,答案在真值左右1m都符合题意,答案不惟一。在本章中误差小于1m就是估算到个位,误差小于10m就是估算到十位。
知识点小结
作业巩固:课本P34面习题2.6 1,2,3.
估算比较大小的方法:
1,两个带根号的无理数比较,直接比较被开方数
如:a>b≥0则
2,无理数和有理数比较,直接把有理数平方或立方与无理数的被开方数比较 如: 和3即比较 和
3,平方法:如 和 即( )2和( )2
4,作差法:两个被比较的数相减的差来和0比较,差大于0则被减数大;小于0则减数大;等于0则两数同样大。
托尔斯泰是俄罗斯最伟大的作家,他曾在作品《一个人需要很多土地吗?》中写了如下一个故事:有一个叫巴河姆的人到草原上去购买土地,卖地的人提出了一个非常奇怪的地价:“每天1000卢布”,意思是谁出1000卢布,那么他从日出到日落走过的路所围成的土地都归他;不过如果在日落之前,买地的人回不到原来的出发点,那他就只好白出1000卢布。巴河姆于是付了1000卢布,等第二天太阳刚刚从地平线上升起,就连忙在草原上大步向前走去。他走了足足有10俄里(1俄里=1.0668公里),这才朝左拐弯;接着又走了许久许久,才再向左拐弯;这样有走了2俄里,这时他发现天色已经不早,而自己离出发点足足还有15俄里的路程,于是只得改变方向,径直朝出发点跑去……最后,他总算如期赶回出发点,却口吐鲜血死去。请你算一算,他这一天共走了多少路?他走过的路围成的土地有多大?(精确到0.1)
挑战自我
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
