14.1 三角形的有关概念(1) 课件(20张PPT)
文档属性
| 名称 | 14.1 三角形的有关概念(1) 课件(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 536.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 15:12:04 | ||
图片预览





文档简介
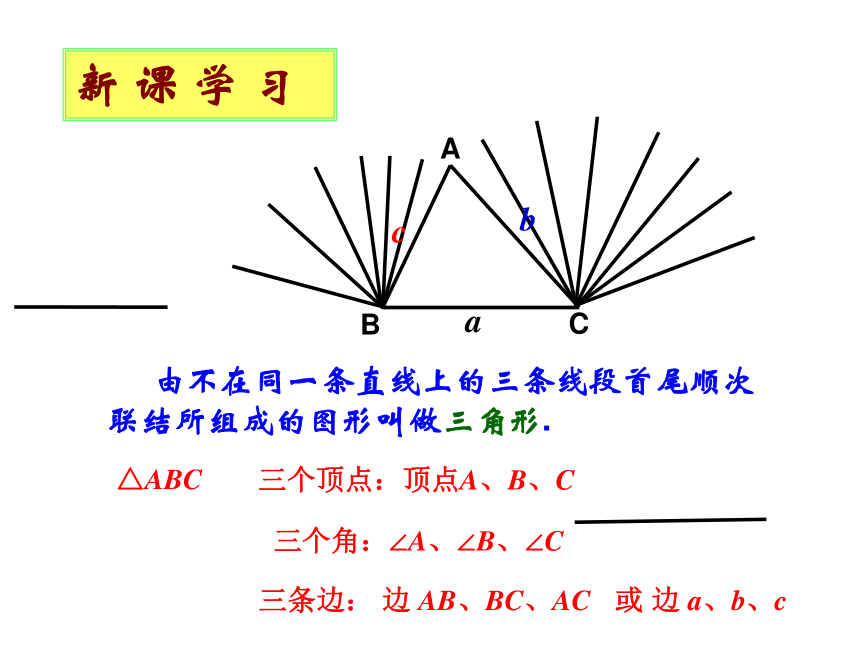
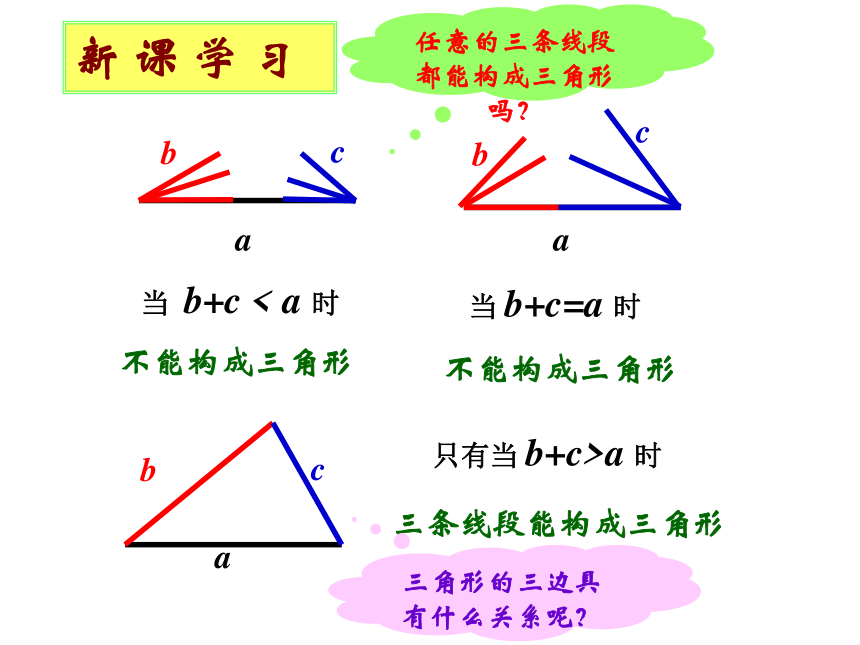
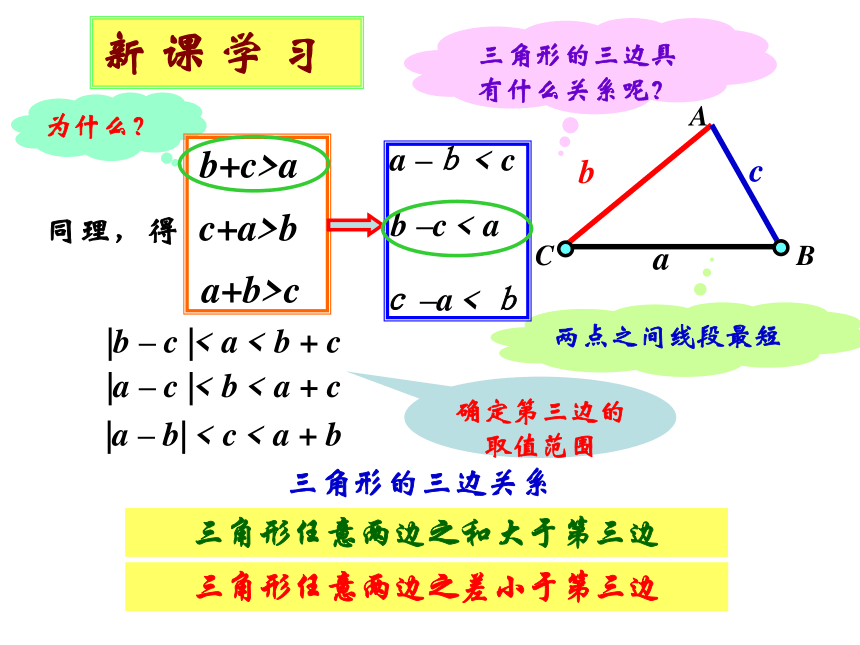
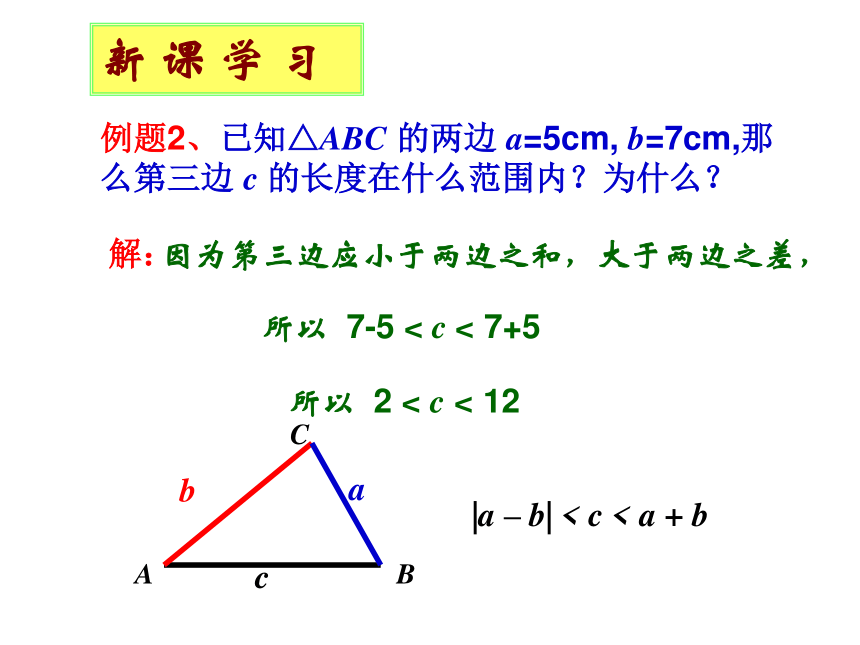
课件20张PPT。14.1 三角形的有关概念(1) 情 景 引 入新 课 学 习 由不在同一条直线上的三条线段首尾顺次联结所组成的图形叫做三角形.△ABC三个角:∠A、∠B、∠C三条边: 边 AB、BC、AC三个顶点:顶点A、B、C或 边 a、b、c新 课 学 习abc当 b+c < a 时不能构成三角形abc当 b+c=a 时 不能构成三角形任意的三条线段都能构成三角形吗?只有当 b+c>a 时 三条线段能构成三角形三角形的三边具有什么关系呢?为什么?新 课 学 习 b+c>a 两点之间线段最短同理,得 a+b>c c+a>b 三角形的三边关系 三角形的三边具有什么关系呢?a –b < cc –a < bb –c < a |b – c |< a < b + c |a – c |< b < a + c |a – b| < c < a + b确定第三边的取值范围新 课 学 习例题1、有两根长度分别为5cm和7cm的木棒,用长度为13cm的木棒与它们能拼成三角形吗?用长度为2cm的木棒呢? 用长度为3cm的木棒呢?解:因为 5+7=12<13, 所以5cm,7cm,13cm的三根木棒不能拼成三角形.因为5+2=7 , 所以5cm,7cm,2cm的三根木棒不能组成三角形.因为5+3>7, 5+7>3, 3+7>5, 所以这三根木棒能组成三角形 .只要判断两条较短的线段之和例题2、已知△ABC 的两边 a=5cm, b=7cm,那么第三边 c 的长度在什么范围内?为什么? 新 课 学 习解:因为第三边应小于两边之和,大于两边之差, |a – b| < c < a + b巩 固 练 习练习:P.74 ——1, 2三角形有几条高、角平分线、中线?新 课 学 习ABCD在一个三角形中,从一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做三角形的高. E 三角形一个内角的角平分分线与这个角的对边相交,这个 角的顶点与交点之间的线段叫做三角形的角平分线.F连接一个顶点及其对边中点的线段叫做三角形的中线三角形的高、角平分线、中线都是线段三角形的角平分线和角的平分线有什么区别三角形的高、角平分线、中线的概念 新 课 学 习D∵AD是△ABC的高,点D为垂足,∴AD⊥BC.反之也成立.E∵AE是△ABC的角平分线,∴∠BAE=∠CAE,或∠BAC=2∠BAE=2∠CAE,或∠BAE=∠CAE= ∠BAC. F反之也成立.∵AF是△ABC的中线,∴BF=CF,或BC=2BF=2CF,或BF=CF= BC.反之也成立.巩 固 练 习练习:P.74 —— 3,4课 堂 小 结1.三角形的概念和表示方法2.三角形的三边关系及其运用 ∠A、∠B、∠C△ABC 边 AB、BC、AC或 边 a、b、c b+c>a, a+b>c. c+a>b,a-c2、画出 课本:P.77 的三角形的中线、角平分线、高 .AFBAFCBADCADBECE2. 用下列各组线段为边能组成三角形的是( )
(A)2cm、4cm、6cm;
(B)2cm、5cm、6cm;
(C)2cm、9cm、6cm;
(D)10cm、4cm、6cm;
D3. 如果三角形的两条边长分别为4cm、6cm,那么第三边的长不可能是( )
(A)4cm; (B)3cm;
(C)9cm; (D)2cm.
B4. 已知△ABC 的两边a=18cm,b=12cm,那么第三边c的长度在什么范围内?为什么?
解:18-12<c1<8+12
即:6cm<c<30cm
判断依据:第三边应小于两边之和30cm,大于两边之差6cm.5. 分别在图中画出△ABC的一条角平分线、一条中线和一条高,并用文字指出你所画的角平分线、中线和高线段AD、AE、AF分别是△ABC的角平分线、中线和高B组
用9根同样的火柴棒在桌面上摆一个三角形(首尾相连,不折断,允许几根连成一根作为一条线段,火柴要全部用完),你能摆出哪几种不同形状的三角形?
答:3种
根据两条较短边之和大于第三边,三边之和为9,
①当最短的边长=1时,三边分别为1,1,7;
1,2,6;
1,3,5;
1,4,4;
能构成三角形的为:1,4,4;
②当最短的边长=2时,三边分别为2,2,5;
2,3,4;③当一边长=3时,三边分别为3,3,3.
(A)2cm、4cm、6cm;
(B)2cm、5cm、6cm;
(C)2cm、9cm、6cm;
(D)10cm、4cm、6cm;
D3. 如果三角形的两条边长分别为4cm、6cm,那么第三边的长不可能是( )
(A)4cm; (B)3cm;
(C)9cm; (D)2cm.
B4. 已知△ABC 的两边a=18cm,b=12cm,那么第三边c的长度在什么范围内?为什么?
解:18-12<c1<8+12
即:6cm<c<30cm
判断依据:第三边应小于两边之和30cm,大于两边之差6cm.5. 分别在图中画出△ABC的一条角平分线、一条中线和一条高,并用文字指出你所画的角平分线、中线和高线段AD、AE、AF分别是△ABC的角平分线、中线和高B组
用9根同样的火柴棒在桌面上摆一个三角形(首尾相连,不折断,允许几根连成一根作为一条线段,火柴要全部用完),你能摆出哪几种不同形状的三角形?
答:3种
根据两条较短边之和大于第三边,三边之和为9,
①当最短的边长=1时,三边分别为1,1,7;
1,2,6;
1,3,5;
1,4,4;
能构成三角形的为:1,4,4;
②当最短的边长=2时,三边分别为2,2,5;
2,3,4;③当一边长=3时,三边分别为3,3,3.
