14.2(1)三角形的内角和 导学案(无答案)
文档属性
| 名称 | 14.2(1)三角形的内角和 导学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 70.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 15:21:18 | ||
图片预览

文档简介
14.2三角形内角和(1)
学习目标:
1、理解和掌握三角形的内角和性质;
2、通过经历操作、归纳、猜测、说理证实的数学研究过程,初步体验感受数学探索、发现的科学历程;
3、体会直观感知与理性思考的联系和区别,懂得直观结论需要说理证实的意义。
学习重点及难点
掌握三角形的内角和性质及运用三角形的内角和性质
学习过程:
一、预习导学
任务一(知识回顾)
1、平行线的性质
2、三角形的分类
3、阅读课本P79--80页的内容
二、尝试研究
任务二(三角形内角和定理)
1、阅读并动手完成课本P79页的“操作”
得出猜想:
思考:猜想可靠吗?
2、验证猜想
①测量方法:
(1)用量角器测量三角形ABC
(2)∠A=_______,∠B=_______,∠C=_______
(3)∠A+∠B+∠C=_______°
②数学推理证明方法
用说理的的方法说明三角形的内角和为180°
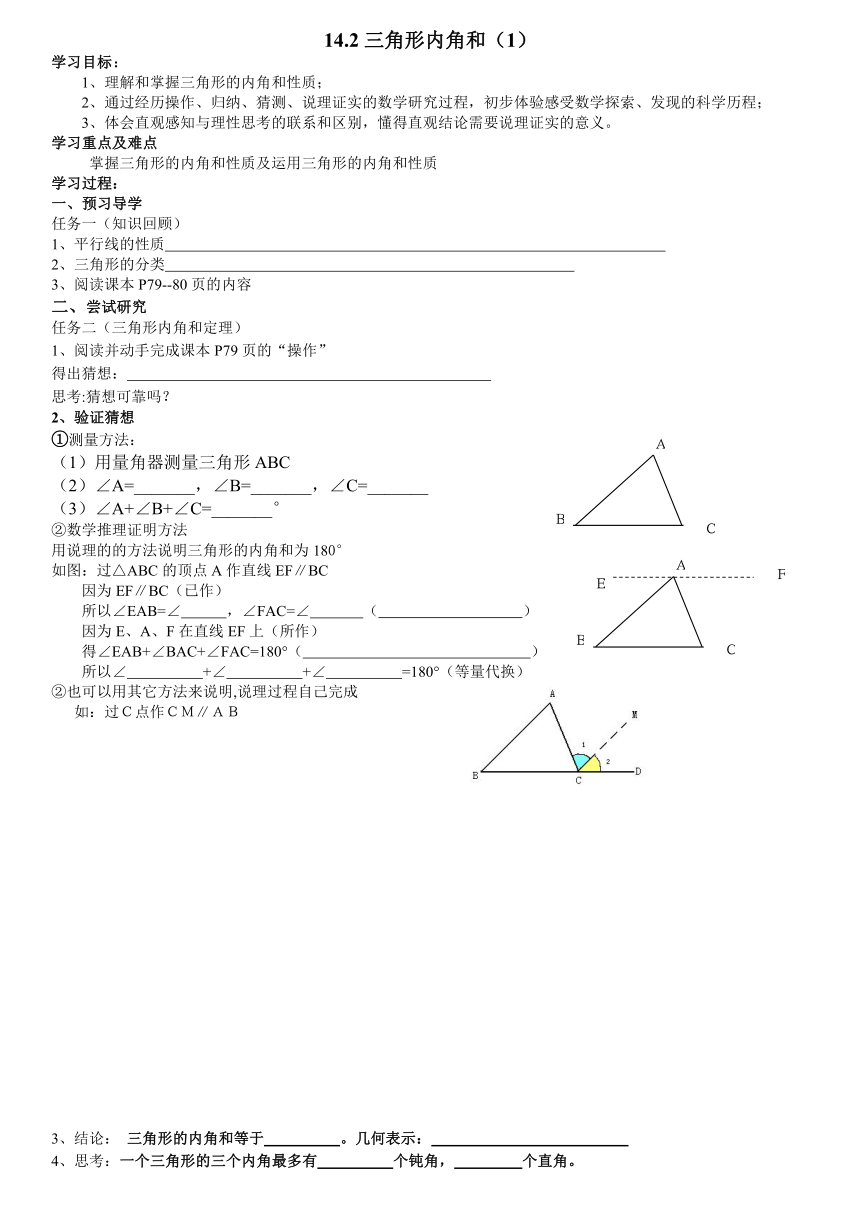
如图:过△ABC的顶点A作直线EF∥BC
因为EF∥BC(已作)
所以∠EAB=∠ ,∠FAC=∠ ( )
因为E、A、F在直线EF上(所作)
得∠EAB+∠BAC+∠FAC=180°( )
所以∠ +∠ +∠ =180°(等量代换)
②也可以用其它方法来说明,说理过程自己完成
如:过C点作CM∥AB
3、结论: 三角形的内角和等于 。几何表示:
4、思考:一个三角形的三个内角最多有 个钝角, 个直角。
5、例1、在⊿ABC中,已知∠B=38°,∠C=52°,求∠A的度数,并判断△ABC的类型.
解:因为∠A、∠B、∠C是△ABC的三个内角(已知),
所以∠A+∠B+∠C=180°( ).
6、例2、在△ABC中,已知∠A:∠B:∠C=3:2:1,求∠A、∠B、∠C的度数.
解:因为∠A:∠B:∠C=3:2:1
所以可设∠A=3x度,∠B =2x度,∠C=x度
三、成果展示
1、判断下列各组角度的角是否是同一个三角形的内角?
⑴ 80°、95°、5°; ⑵ 60°、20°、90°;
⑶ 35°、40°、105°; ⑷ 73°、50°、57°.
2、判断正误:
(1)三角形的三个内角中最多有一个钝角。 ( )
(2)三角形的三个内角中至少有两个锐角。 ( )
(3)有两个内角分别为50°和20°的三角形一定是钝角三角形。 ( )
(4)直角三角形中两锐角和为90°。 ( )
3、在△ABC中 ,若∠A=45°,∠B=30°,则∠C= .
变式1:在△ ABC中,∠A=45°,∠B= 2∠C,求∠B、 ∠C的度数。
变式2:在△ ABC中,∠A=∠B= 2∠C,求∠B、 ∠C的度数。
变式3:在△ ABC中,∠A:∠B:∠C=2:3:5,求∠A 、∠B、 ∠C的度数。
变式4:在△ ABC中,∠A+ ∠B = ∠C ,求∠C的度数。
四、自我检测
1、在△ABC中,若∠A=80°,∠C=20°,则∠B=____;若∠A=80°,∠B=∠C,则∠C=____。
已知△ABC的三个内角的度数之比∠A∶∠B∶∠C=2∶3∶5,则∠A= ∠B=__ __,∠C=___ 。
3、如图,在△ABC中∠C=60°,∠B=50°,AD是∠BAC的平分线,
则∠BAD= ,∠DAC= ,∠ADB=___ __。
4、在△ABC中,∠A+∠B=130°,∠A﹣∠B=20°则∠A=____ ∠B=____,∠C=____
5、在△ABC中,∠A=∠B﹢∠C,则∠A=____ ∠B=____,∠C=____
6、在△ABC中,∠A=55°,∠B比∠C大25°,则∠B的度数为 ( ).
(A)50° (B)75°
(C)100° (D)125°
7、直角三角形两锐角的角平分线交成的角的度数是 ( )
A.45° B 、135° C 、 45°或 135° D、以上均不正确
8、如图,AC∥DE,若∠ABC = 70°∠E = 50°∠D = 75°,求∠A、∠ABD的度数
9、如图:在△ABC中,已知角平分线BD、CE相交于点F,
(1)如果∠A=35°,求∠BFC的度数
(2)如果∠A=100°,求∠BFC的度数
(3)由上两问,∠A和∠BFC有什么数量关系吗?并写出说理过程。
学习目标:
1、理解和掌握三角形的内角和性质;
2、通过经历操作、归纳、猜测、说理证实的数学研究过程,初步体验感受数学探索、发现的科学历程;
3、体会直观感知与理性思考的联系和区别,懂得直观结论需要说理证实的意义。
学习重点及难点
掌握三角形的内角和性质及运用三角形的内角和性质
学习过程:
一、预习导学
任务一(知识回顾)
1、平行线的性质
2、三角形的分类
3、阅读课本P79--80页的内容
二、尝试研究
任务二(三角形内角和定理)
1、阅读并动手完成课本P79页的“操作”
得出猜想:
思考:猜想可靠吗?
2、验证猜想
①测量方法:
(1)用量角器测量三角形ABC
(2)∠A=_______,∠B=_______,∠C=_______
(3)∠A+∠B+∠C=_______°
②数学推理证明方法
用说理的的方法说明三角形的内角和为180°
如图:过△ABC的顶点A作直线EF∥BC
因为EF∥BC(已作)
所以∠EAB=∠ ,∠FAC=∠ ( )
因为E、A、F在直线EF上(所作)
得∠EAB+∠BAC+∠FAC=180°( )
所以∠ +∠ +∠ =180°(等量代换)
②也可以用其它方法来说明,说理过程自己完成
如:过C点作CM∥AB
3、结论: 三角形的内角和等于 。几何表示:
4、思考:一个三角形的三个内角最多有 个钝角, 个直角。
5、例1、在⊿ABC中,已知∠B=38°,∠C=52°,求∠A的度数,并判断△ABC的类型.
解:因为∠A、∠B、∠C是△ABC的三个内角(已知),
所以∠A+∠B+∠C=180°( ).
6、例2、在△ABC中,已知∠A:∠B:∠C=3:2:1,求∠A、∠B、∠C的度数.
解:因为∠A:∠B:∠C=3:2:1
所以可设∠A=3x度,∠B =2x度,∠C=x度
三、成果展示
1、判断下列各组角度的角是否是同一个三角形的内角?
⑴ 80°、95°、5°; ⑵ 60°、20°、90°;
⑶ 35°、40°、105°; ⑷ 73°、50°、57°.
2、判断正误:
(1)三角形的三个内角中最多有一个钝角。 ( )
(2)三角形的三个内角中至少有两个锐角。 ( )
(3)有两个内角分别为50°和20°的三角形一定是钝角三角形。 ( )
(4)直角三角形中两锐角和为90°。 ( )
3、在△ABC中 ,若∠A=45°,∠B=30°,则∠C= .
变式1:在△ ABC中,∠A=45°,∠B= 2∠C,求∠B、 ∠C的度数。
变式2:在△ ABC中,∠A=∠B= 2∠C,求∠B、 ∠C的度数。
变式3:在△ ABC中,∠A:∠B:∠C=2:3:5,求∠A 、∠B、 ∠C的度数。
变式4:在△ ABC中,∠A+ ∠B = ∠C ,求∠C的度数。
四、自我检测
1、在△ABC中,若∠A=80°,∠C=20°,则∠B=____;若∠A=80°,∠B=∠C,则∠C=____。
已知△ABC的三个内角的度数之比∠A∶∠B∶∠C=2∶3∶5,则∠A= ∠B=__ __,∠C=___ 。
3、如图,在△ABC中∠C=60°,∠B=50°,AD是∠BAC的平分线,
则∠BAD= ,∠DAC= ,∠ADB=___ __。
4、在△ABC中,∠A+∠B=130°,∠A﹣∠B=20°则∠A=____ ∠B=____,∠C=____
5、在△ABC中,∠A=∠B﹢∠C,则∠A=____ ∠B=____,∠C=____
6、在△ABC中,∠A=55°,∠B比∠C大25°,则∠B的度数为 ( ).
(A)50° (B)75°
(C)100° (D)125°
7、直角三角形两锐角的角平分线交成的角的度数是 ( )
A.45° B 、135° C 、 45°或 135° D、以上均不正确
8、如图,AC∥DE,若∠ABC = 70°∠E = 50°∠D = 75°,求∠A、∠ABD的度数
9、如图:在△ABC中,已知角平分线BD、CE相交于点F,
(1)如果∠A=35°,求∠BFC的度数
(2)如果∠A=100°,求∠BFC的度数
(3)由上两问,∠A和∠BFC有什么数量关系吗?并写出说理过程。
