14.3(1)全等三角形的概念与性质 课件(16张PPT)
文档属性
| 名称 | 14.3(1)全等三角形的概念与性质 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览



文档简介
课件16张PPT。§14.3全等三角形的概念与性质(1)新课引入问:图形有哪些基本运动?答:图形的基本运动有平移、旋转、翻折.问:图形运动后什么改变,什么没有变?答:图形经过运动后,位置发生了改变,但形状、大小
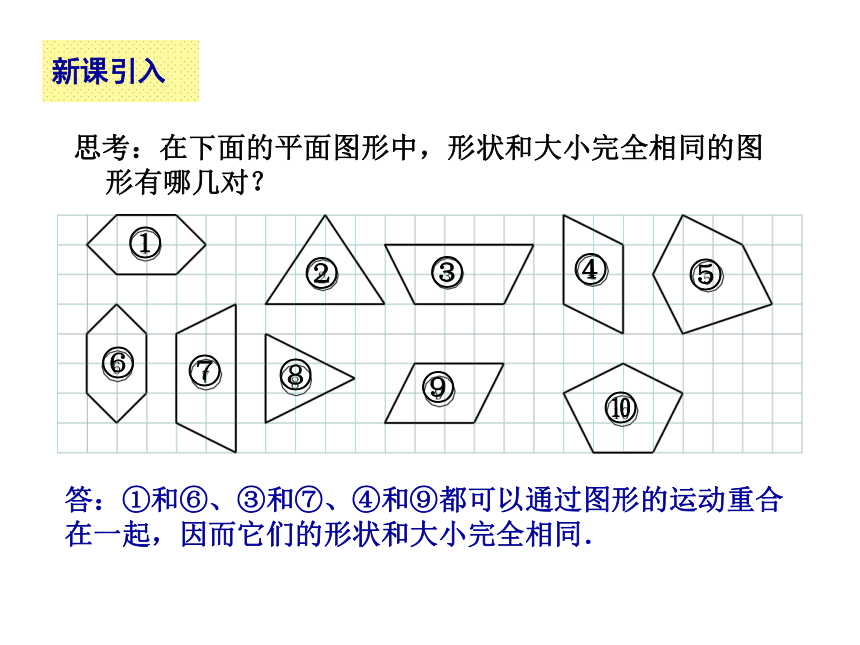
没有改变.新课引入思考:在下面的平面图形中,形状和大小完全相同的图形有哪几对?答:①和⑥、③和⑦、④和⑨都可以通过图形的运动重合
在一起,因而它们的形状和大小完全相同. ①②⑧⑦⑥⑤④③⑩⑨新知探究想一想:下列三对图形,每对图形中的一个图形经过某
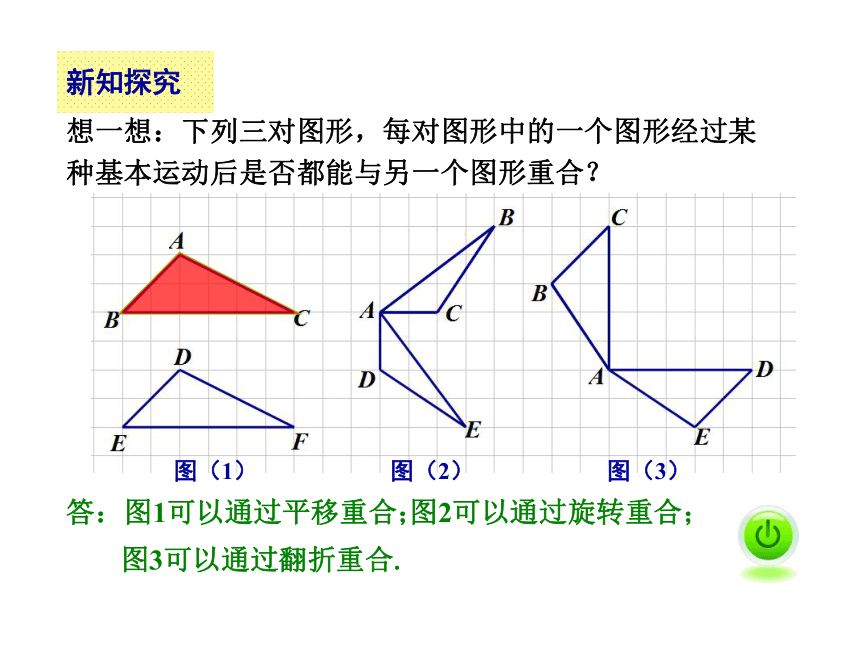
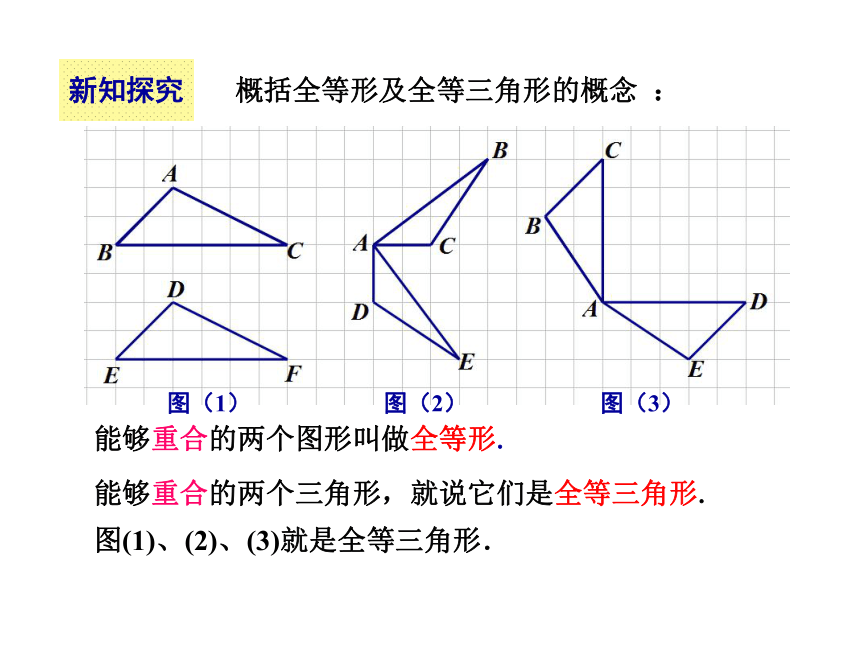
种基本运动后是否都能与另一个图形重合?答:图1可以通过平移重合;图2可以通过旋转重合;图3可以通过翻折重合.图(1) 图(2) 图(3)新知探究能够重合的两个图形叫做全等形.能够重合的两个三角形,就说它们是全等三角形. 图(1)、(2)、(3)就是全等三角形.概括全等形及全等三角形的概念 :图(1) 图(2) 图(3)新知探究自主探索:三角形有六个元素,既然两个全等三角形能
重合,是否可以归纳全等三角形的对应顶点、对应边、
对应角的概念. 填空:
两个全等三角形,经过运动后一定 ,
互相 的 叫做对应顶点;
叫做对应边;
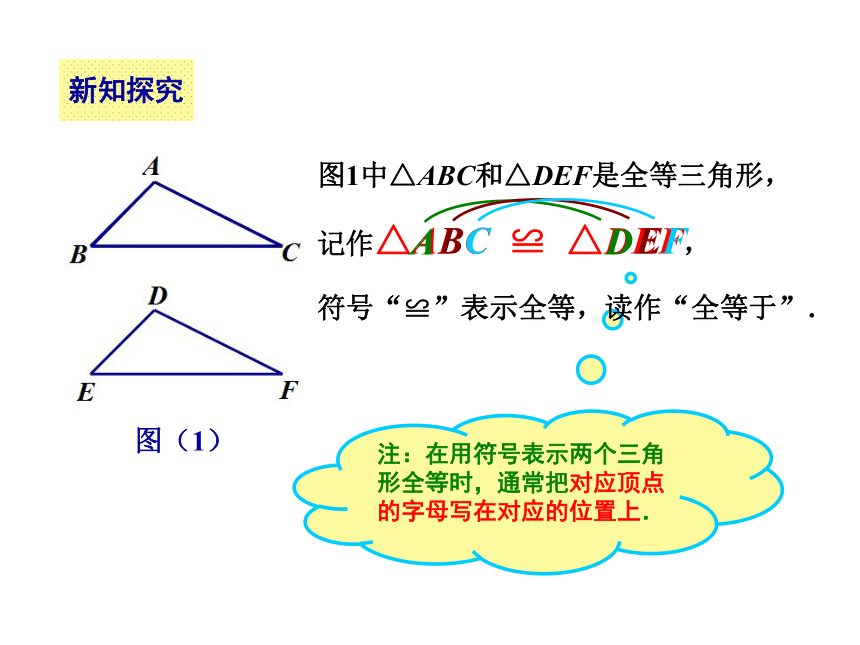
叫做对应角. 重合重合顶点互相重合的边互相重合的角新知探究图1中△ABC和△DEF是全等三角形,记作△ABC ≌ △DEF,注:在用符号表示两个三角形全等时,通常把对应顶点的字母写在对应的位置上.图(1)符号“≌”表示全等,读作“全等于”.练习一请用数学符号表示图2中两个全等三角形,
并指出其对应顶点、对应边、对应角. 答:△ABC≌△AED,对应顶点:点A与点A、
点B与点E、
点C与点 D ;对应边:AB与AE、
AC与AD、
BC与ED;对应角:∠BAC与∠EAD、
∠B与∠E、
∠C与∠D.注:在用符号表示两个三角形全等时,通常把对应顶点的字母写在对应的位置上.△ABC≌△AED,你能根据图(2)中全等三角形的对应边、对应角的数量关系,归纳全等三角形的性质吗? 图(2)新知探究全等三角形的性质 ∵△ABC ≌ △DEF
∴AB=DE、AC=DF、BC=EF∠A=∠D、∠B=∠E、∠C=∠F(全等三角形的对应边相等),(全等三角形的对应角相等).(已知) ,练习二图(3)ADCB全等三角形的对应边相等全等三角形的对应角相等∠1∠E ∴∠A =∠D,∠B =∠E
(全等三角形的对应角相等),
AB = DE
(全等三角形的对应边相等). ∠F =180°-∠D-∠E= 50° 可以得到哪些结论? ∠A=∠D AB=DE
∠B=∠E BC=EF
∠C=∠F AC=DF可以得到哪些结论?2cm如何求∠F ? 解:∵△ABC ≌ △DEF(已知),∵∠A = 60°,∠B = 70°,
AB= 2 cm (已知),∴∠D = 60°,∠E = 70°,
DE = 2 cm(等量代换). ∵∠D +∠E +∠F = 180°
(三角形的内角和等于180°),∴∠F = 50°(等式性质). ∴DE = 2 cm,∠D = 60°,
∠F = 50°. 还有其他的解法吗? 练习三书P 88页 练习14.3(1) 补充练习 图中给出的每对三角形都是全等三角形.用符号
表示各对全等三角形,并指出其对应边和对应角. 小 结1.全等形、全等三角形的概念.
能够重合的两个图形叫做全等形.能够重合的两个三角形,就说它们是全等三角形.
2.全等三角形的对应边、对应角.
两个全等三角形,经过运动后一定重合,互相重合的顶点叫做对应顶点;互相重合的边叫做对应边;互相重合的角叫做对应角.
3.全等三角形的性质.
全等三角形的对应边相等、对应角相等.
布置作业练习册 14.3(1) 谢谢观赏!
没有改变.新课引入思考:在下面的平面图形中,形状和大小完全相同的图形有哪几对?答:①和⑥、③和⑦、④和⑨都可以通过图形的运动重合
在一起,因而它们的形状和大小完全相同. ①②⑧⑦⑥⑤④③⑩⑨新知探究想一想:下列三对图形,每对图形中的一个图形经过某
种基本运动后是否都能与另一个图形重合?答:图1可以通过平移重合;图2可以通过旋转重合;图3可以通过翻折重合.图(1) 图(2) 图(3)新知探究能够重合的两个图形叫做全等形.能够重合的两个三角形,就说它们是全等三角形. 图(1)、(2)、(3)就是全等三角形.概括全等形及全等三角形的概念 :图(1) 图(2) 图(3)新知探究自主探索:三角形有六个元素,既然两个全等三角形能
重合,是否可以归纳全等三角形的对应顶点、对应边、
对应角的概念. 填空:
两个全等三角形,经过运动后一定 ,
互相 的 叫做对应顶点;
叫做对应边;
叫做对应角. 重合重合顶点互相重合的边互相重合的角新知探究图1中△ABC和△DEF是全等三角形,记作△ABC ≌ △DEF,注:在用符号表示两个三角形全等时,通常把对应顶点的字母写在对应的位置上.图(1)符号“≌”表示全等,读作“全等于”.练习一请用数学符号表示图2中两个全等三角形,
并指出其对应顶点、对应边、对应角. 答:△ABC≌△AED,对应顶点:点A与点A、
点B与点E、
点C与点 D ;对应边:AB与AE、
AC与AD、
BC与ED;对应角:∠BAC与∠EAD、
∠B与∠E、
∠C与∠D.注:在用符号表示两个三角形全等时,通常把对应顶点的字母写在对应的位置上.△ABC≌△AED,你能根据图(2)中全等三角形的对应边、对应角的数量关系,归纳全等三角形的性质吗? 图(2)新知探究全等三角形的性质 ∵△ABC ≌ △DEF
∴AB=DE、AC=DF、BC=EF∠A=∠D、∠B=∠E、∠C=∠F(全等三角形的对应边相等),(全等三角形的对应角相等).(已知) ,练习二图(3)ADCB全等三角形的对应边相等全等三角形的对应角相等∠1∠E ∴∠A =∠D,∠B =∠E
(全等三角形的对应角相等),
AB = DE
(全等三角形的对应边相等). ∠F =180°-∠D-∠E= 50° 可以得到哪些结论? ∠A=∠D AB=DE
∠B=∠E BC=EF
∠C=∠F AC=DF可以得到哪些结论?2cm如何求∠F ? 解:∵△ABC ≌ △DEF(已知),∵∠A = 60°,∠B = 70°,
AB= 2 cm (已知),∴∠D = 60°,∠E = 70°,
DE = 2 cm(等量代换). ∵∠D +∠E +∠F = 180°
(三角形的内角和等于180°),∴∠F = 50°(等式性质). ∴DE = 2 cm,∠D = 60°,
∠F = 50°. 还有其他的解法吗? 练习三书P 88页 练习14.3(1) 补充练习 图中给出的每对三角形都是全等三角形.用符号
表示各对全等三角形,并指出其对应边和对应角. 小 结1.全等形、全等三角形的概念.
能够重合的两个图形叫做全等形.能够重合的两个三角形,就说它们是全等三角形.
2.全等三角形的对应边、对应角.
两个全等三角形,经过运动后一定重合,互相重合的顶点叫做对应顶点;互相重合的边叫做对应边;互相重合的角叫做对应角.
3.全等三角形的性质.
全等三角形的对应边相等、对应角相等.
布置作业练习册 14.3(1) 谢谢观赏!
