14.2(1)三角形的内角和 课件(16张PPT)
文档属性
| 名称 | 14.2(1)三角形的内角和 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 306.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览





文档简介
课件16张PPT。14.2(1)三角形的内角和问题1: 三角形的三边有什么关系? 三角形任意两边的和大于第三边.问题2: 三角形的三个内角又有什么
关系呢? 三角形任意两边的差小于第三边.等边三角形的三个内角分别是多少度?一副三角尺中的两个三角形的三个角分别是多少度?三个内角的和是多少度? 两个三角形的内角和分别是多少度?60o60o60o180o90o45o45o90o30o60o180o任意一个三角形的三个内角之间的关系?猜想三角形的三个内角和等于180° 如何验证三角形的内角和等于180°? 方法二:
可裁下它的三个角,拼在一起,构成平角180°方法一:
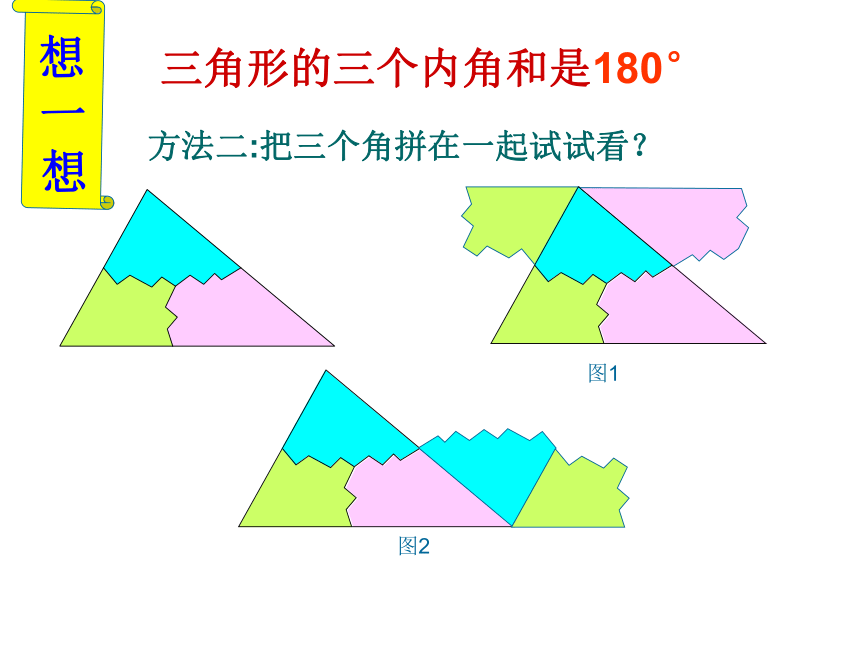
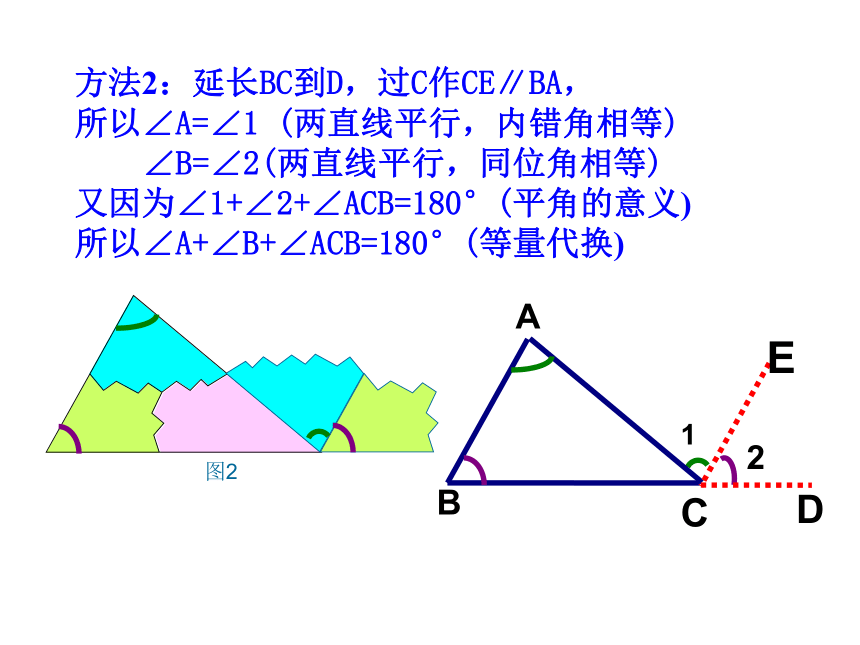
量角器量出三个角并相加,得出结论和为180°测量法想一想拼叠法想一想三角形的三个内角和是180° 方法二:把三个角拼在一起试试看?图1图2方法2:延长BC到D,过C作CE∥BA,
所以∠A=∠1 (两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又因为∠1+∠2+∠ACB=180°(平角的意义)
所以∠A+∠B+∠ACB=180°(等量代换)21EDCBA图2三角形的内角和性质文字语言:三角形的内角和等于180°
符号语言:
因为∠A、∠B、∠C是△ABC的三个内角(已知)
所以∠A+∠B+∠C=180°(三角形的内角和等
于180°)结论小试牛刀⑴ 80°、95°、5°; ⑵ 60°、20°、90°;1、判断下列各组角度的角是否是同一个三角形的内角? (√)(×)2、求下列各三角形中∠C的度数.∠C=75°∠C=40°∠C=30°3、辨析:
(1)三角形的三个内角中最多有一个钝角。( )
(2)一个三角形最多有一个直角。( )
(3)三角形的三个内角中至少有两个锐角。( )√√√例1、在△ABC中,已知∠B=35°,∠C=55°,
求∠A的度数,并判断△ABC的类型。解:因为∠A、∠B、∠C是△ABC的三个内角 (已知),
所以∠A+∠B+∠C=180°(三角形的内角和等于180°)
由∠B=35°, ∠C=55° (已知),
得∠A=180°-∠B-∠C=180°-35°-55° =90°(等式性质).
所以△ABC是直角三角形.例题精析例2、在△ABC中,已知∠A:∠B:∠C=1:2:3, 求∠A的度数,并说明△ABC的形状.变式:在△ABC中, 已知∠B=60°,
∠A:∠C=1:2,求∠A的度数.例题精析解: 由题意,可设∠A、∠B、∠C的度数分别为x、2x、3x
因为∠A、∠B、∠C是△ABC的三个内角 (已知)
所以∠A+∠B+∠C=180°(三角形的内角和等于180°)
即 x+2x+3x=180
解得 x=30
所以∠A=30°,∠B=60° , ∠C=90°
所以△ABC是直角三角形(2)当∠ABC+∠ACB=100O时,∠BOC= .(1)当∠ABC=40O ,∠ACB=60O时,∠BOC= .如图,在△ABC中,已知角平分线BF、CE相交于点O,拓展应用(3)当∠A=80O时,∠BOC= .(4)当∠A=nO时,∠BOC= .这节课你有哪些收获?反馈练习1、下列各组角能是同一个三角形的内角的是( )A. 20°、50°、20°; B. 40°、60°、90°; C. 100°、40°、60°; D. 15°、150°、15°;D2、在△ABC中,如果∠A=35°,∠B=40°,
那么∠C=_____,△ABC是_____三角形.3、在△ABC中,如果∠A:∠B:∠C =2:3:4,
那么△ABC是_____三角形.105°钝角锐角作业:校本14.2(1)三角形的内角和
必做题:1-9
选做题:10、11
关系呢? 三角形任意两边的差小于第三边.等边三角形的三个内角分别是多少度?一副三角尺中的两个三角形的三个角分别是多少度?三个内角的和是多少度? 两个三角形的内角和分别是多少度?60o60o60o180o90o45o45o90o30o60o180o任意一个三角形的三个内角之间的关系?猜想三角形的三个内角和等于180° 如何验证三角形的内角和等于180°? 方法二:
可裁下它的三个角,拼在一起,构成平角180°方法一:
量角器量出三个角并相加,得出结论和为180°测量法想一想拼叠法想一想三角形的三个内角和是180° 方法二:把三个角拼在一起试试看?图1图2方法2:延长BC到D,过C作CE∥BA,
所以∠A=∠1 (两直线平行,内错角相等)
∠B=∠2(两直线平行,同位角相等)
又因为∠1+∠2+∠ACB=180°(平角的意义)
所以∠A+∠B+∠ACB=180°(等量代换)21EDCBA图2三角形的内角和性质文字语言:三角形的内角和等于180°
符号语言:
因为∠A、∠B、∠C是△ABC的三个内角(已知)
所以∠A+∠B+∠C=180°(三角形的内角和等
于180°)结论小试牛刀⑴ 80°、95°、5°; ⑵ 60°、20°、90°;1、判断下列各组角度的角是否是同一个三角形的内角? (√)(×)2、求下列各三角形中∠C的度数.∠C=75°∠C=40°∠C=30°3、辨析:
(1)三角形的三个内角中最多有一个钝角。( )
(2)一个三角形最多有一个直角。( )
(3)三角形的三个内角中至少有两个锐角。( )√√√例1、在△ABC中,已知∠B=35°,∠C=55°,
求∠A的度数,并判断△ABC的类型。解:因为∠A、∠B、∠C是△ABC的三个内角 (已知),
所以∠A+∠B+∠C=180°(三角形的内角和等于180°)
由∠B=35°, ∠C=55° (已知),
得∠A=180°-∠B-∠C=180°-35°-55° =90°(等式性质).
所以△ABC是直角三角形.例题精析例2、在△ABC中,已知∠A:∠B:∠C=1:2:3, 求∠A的度数,并说明△ABC的形状.变式:在△ABC中, 已知∠B=60°,
∠A:∠C=1:2,求∠A的度数.例题精析解: 由题意,可设∠A、∠B、∠C的度数分别为x、2x、3x
因为∠A、∠B、∠C是△ABC的三个内角 (已知)
所以∠A+∠B+∠C=180°(三角形的内角和等于180°)
即 x+2x+3x=180
解得 x=30
所以∠A=30°,∠B=60° , ∠C=90°
所以△ABC是直角三角形(2)当∠ABC+∠ACB=100O时,∠BOC= .(1)当∠ABC=40O ,∠ACB=60O时,∠BOC= .如图,在△ABC中,已知角平分线BF、CE相交于点O,拓展应用(3)当∠A=80O时,∠BOC= .(4)当∠A=nO时,∠BOC= .这节课你有哪些收获?反馈练习1、下列各组角能是同一个三角形的内角的是( )A. 20°、50°、20°; B. 40°、60°、90°; C. 100°、40°、60°; D. 15°、150°、15°;D2、在△ABC中,如果∠A=35°,∠B=40°,
那么∠C=_____,△ABC是_____三角形.3、在△ABC中,如果∠A:∠B:∠C =2:3:4,
那么△ABC是_____三角形.105°钝角锐角作业:校本14.2(1)三角形的内角和
必做题:1-9
选做题:10、11
