14.2(1)三角形的内角和 课件(13张PPT)
文档属性
| 名称 | 14.2(1)三角形的内角和 课件(13张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 221.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 16:17:29 | ||
图片预览




文档简介
课件13张PPT。观察 你知道这三个三角形的内角分别等于多少度吗?并判断这三个三角形是属于哪种类型的三角形?其内角和等于多少度?猜想 已知任意一个三角形,猜测其内角和等于多少度?小
小
数
学
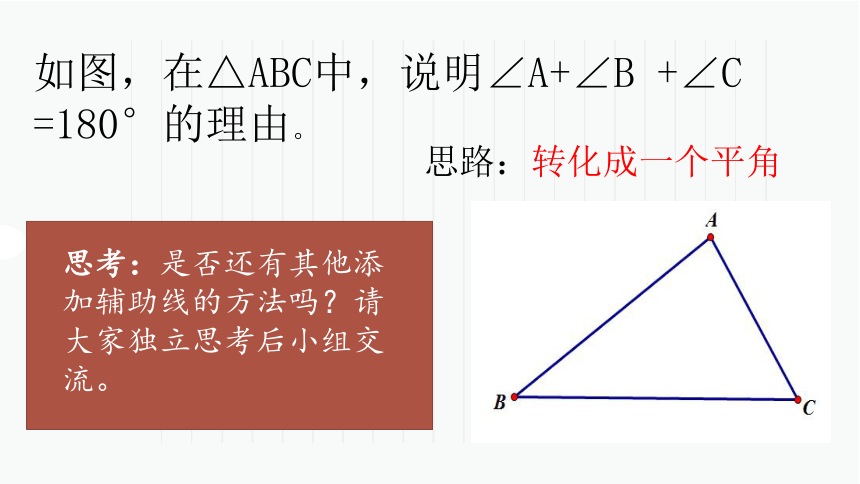
史 公元前3世纪,古希腊数学家欧几里德在《几何原本》中提到“三角形的内角和等于180°” 在300多年前,一个法国数学家帕斯卡也发现了三角形的内角和等于180°,当时他才12岁。14.2(1)三角形的内角和操作方法1:测量法方法2:拼凑法方法3:折叠法拿出准备好的三角形,动手操作验证你的猜想吧!如图,在△ABC中,说明∠A+∠B +∠C =180°的理由。思考:是否还有其他添加辅助线的方法吗?请大家独立思考后小组交流。 思路:转化成一个平角符号语言:
∵∠A、∠B、∠C是△ABC的三个内角(已知)
∴∠A+∠B+∠C=180°
(三角形的内角和等于180°)三角形的内角和性质归纳文字语言:三角形的内角和等于180° 判断下列各组角度的角是否是同一个三角形的内角?若能,判断属于哪种类型的三角形?
(1)60°,20°,90° ( )
(2)35°,40°,105° ( )
(3)90°,40°,50° ( )
(4)73°,50°,57° ( )
(5)0°,90°,90° ( )试一试××√√√思考 一个三角形的三个内角中,最多有几个钝角?最多有几个直角?最多有几个锐角?例1 在⊿ABC中,已知∠B=35°,∠C=55°,求∠A的度数,并判断⊿ABC的类型.例题变式2 在⊿ABC中,已知∠A:∠B:∠C=1:2:3,求∠A、∠B、∠C的度数.变式1 已知⊿ABC中两个内角的度数,试求第三个内角的度数,并判断⊿ABC的类型:
(1)∠A=30°,∠B=40°,∠C=______.
(2)∠B=32°,∠C=58°,∠A=______.
(3)∠A=60°,∠C=50°,∠B=______.1、在△ABC中,已知∠A:∠B:∠C=2:3:4,求∠A、∠B、∠C的度数.并判断△ABC的类型。
2、在⊿ABC中,已知∠A=60°,∠A=3∠B,求∠C的度数,并判断⊿ABC的类型.练习小结通过本节课的学习,你有什么收获吗?1、验证三角形的内角和的性质的实验方法。
2、三角形的内角和的性质。
小
数
学
史 公元前3世纪,古希腊数学家欧几里德在《几何原本》中提到“三角形的内角和等于180°” 在300多年前,一个法国数学家帕斯卡也发现了三角形的内角和等于180°,当时他才12岁。14.2(1)三角形的内角和操作方法1:测量法方法2:拼凑法方法3:折叠法拿出准备好的三角形,动手操作验证你的猜想吧!如图,在△ABC中,说明∠A+∠B +∠C =180°的理由。思考:是否还有其他添加辅助线的方法吗?请大家独立思考后小组交流。 思路:转化成一个平角符号语言:
∵∠A、∠B、∠C是△ABC的三个内角(已知)
∴∠A+∠B+∠C=180°
(三角形的内角和等于180°)三角形的内角和性质归纳文字语言:三角形的内角和等于180° 判断下列各组角度的角是否是同一个三角形的内角?若能,判断属于哪种类型的三角形?
(1)60°,20°,90° ( )
(2)35°,40°,105° ( )
(3)90°,40°,50° ( )
(4)73°,50°,57° ( )
(5)0°,90°,90° ( )试一试××√√√思考 一个三角形的三个内角中,最多有几个钝角?最多有几个直角?最多有几个锐角?例1 在⊿ABC中,已知∠B=35°,∠C=55°,求∠A的度数,并判断⊿ABC的类型.例题变式2 在⊿ABC中,已知∠A:∠B:∠C=1:2:3,求∠A、∠B、∠C的度数.变式1 已知⊿ABC中两个内角的度数,试求第三个内角的度数,并判断⊿ABC的类型:
(1)∠A=30°,∠B=40°,∠C=______.
(2)∠B=32°,∠C=58°,∠A=______.
(3)∠A=60°,∠C=50°,∠B=______.1、在△ABC中,已知∠A:∠B:∠C=2:3:4,求∠A、∠B、∠C的度数.并判断△ABC的类型。
2、在⊿ABC中,已知∠A=60°,∠A=3∠B,求∠C的度数,并判断⊿ABC的类型.练习小结通过本节课的学习,你有什么收获吗?1、验证三角形的内角和的性质的实验方法。
2、三角形的内角和的性质。
