14.5 等腰三角形的性质 课件(14张PPT)
文档属性
| 名称 | 14.5 等腰三角形的性质 课件(14张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 462.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览



文档简介
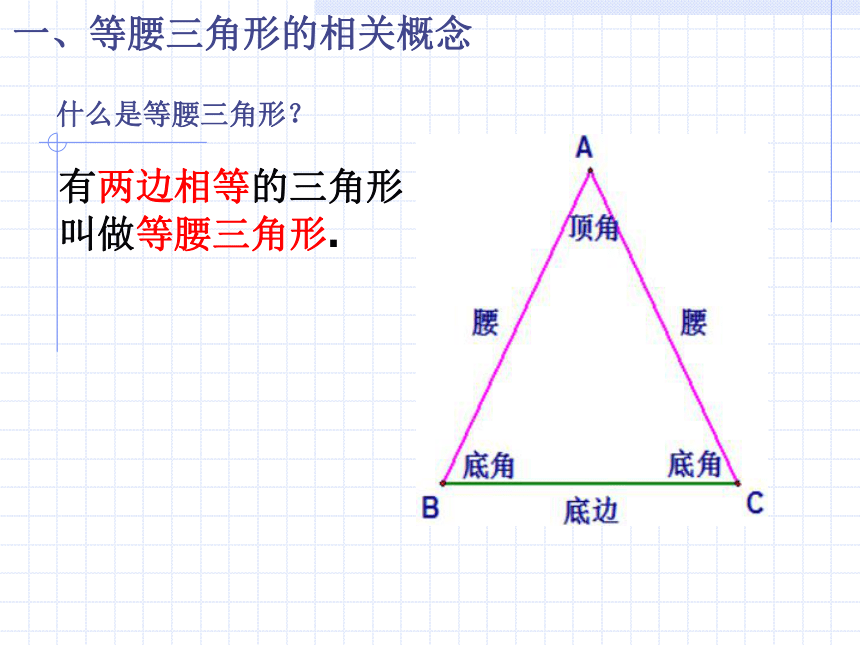
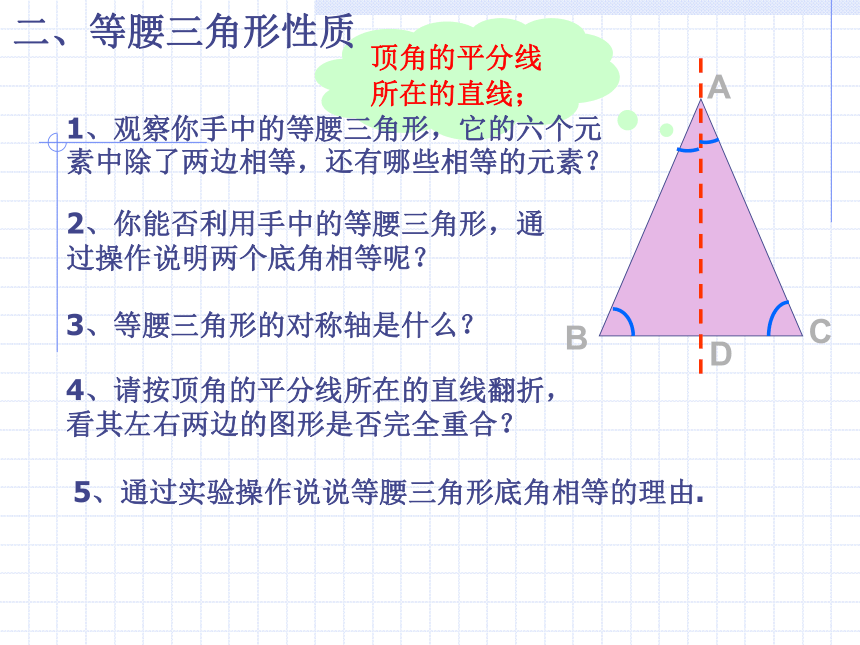
课件14张PPT。观察14.5等腰三角形的性质一、等腰三角形的相关概念 什么是等腰三角形? 有两边相等的三角形叫做等腰三角形.顶角的平分线所在的直线; 二、等腰三角形性质ABCD1、观察你手中的等腰三角形,它的六个元素中除了两边相等,还有哪些相等的元素?2、你能否利用手中的等腰三角形,通过操作说明两个底角相等呢? 3、等腰三角形的对称轴是什么?4、请按顶角的平分线所在的直线翻折,看其左右两边的图形是否完全重合? 5、通过实验操作说说等腰三角形底角相等的理由. 二、等腰三角形性质(1)等腰三角形是轴对称图形,顶角平分线所在的直线是它的对称轴;ABD通过操作发现:(2)等腰三角形的两个底角相等.CB如果不进行操作,你能否用几何说理来说明等腰三角形的两个底角相等呢? 二、等腰三角形性质ADCB12已知△ABC是等腰三角形,且AB=AC,
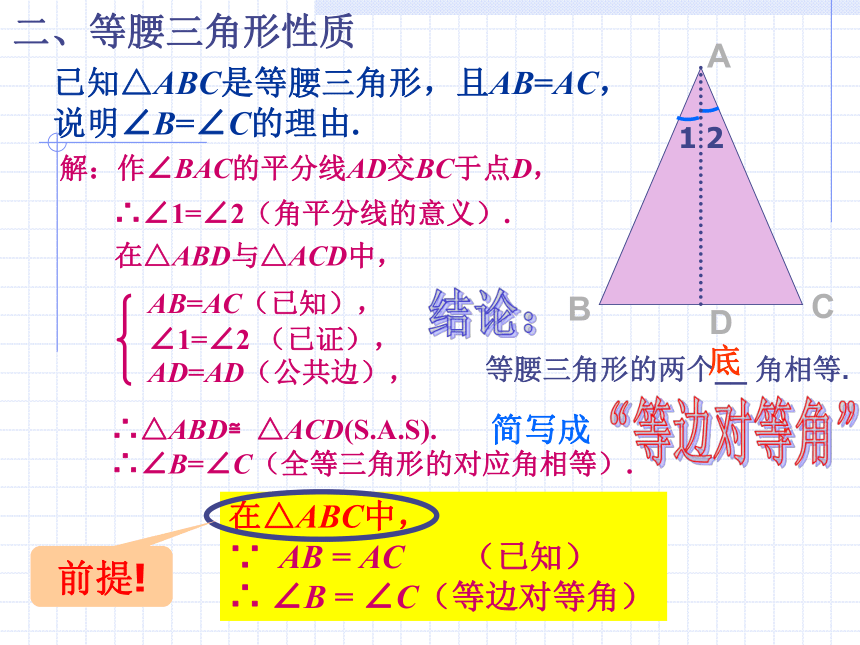
说明∠B=∠C的理由.解:作∠BAC的平分线AD交BC于点D, ∴∠1=∠2(角平分线的意义).在△ABD与△ACD中,AB=AC(已知),
∠1=∠2 (已证),
AD=AD(公共边), ∴△ABD≌△ACD(S.A.S).
∴∠B=∠C(全等三角形的对应角相等).结论:等腰三角形的两个__ 角相等.底在△ABC中,
∵ AB = AC (已知)
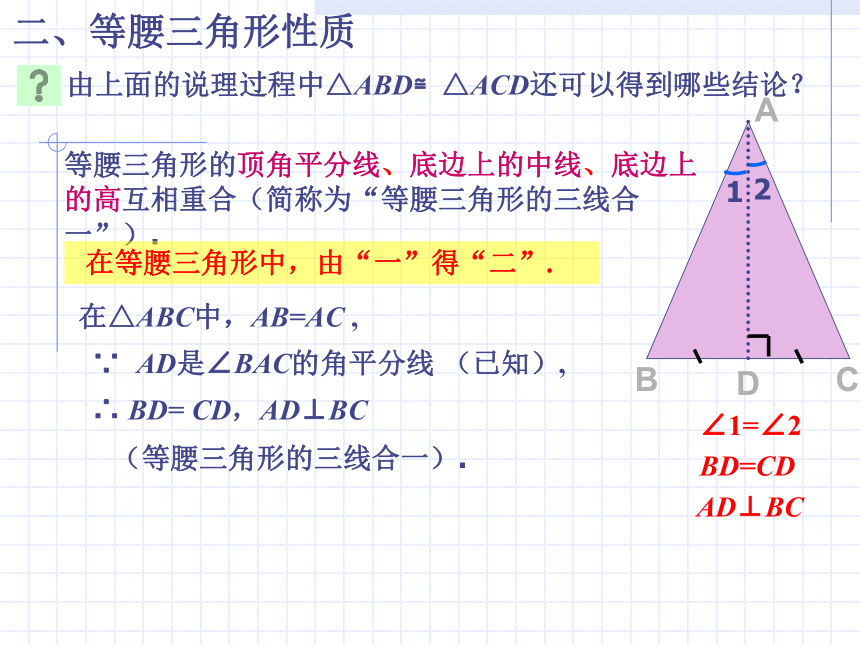
∴ ∠B = ∠C(等边对等角)前提!二、等腰三角形性质ADCB12由上面的说理过程中△ABD≌△ACD还可以得到哪些结论? BD=CD AD⊥BC 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“等腰三角形的三线合一”). ∠1=∠2 在等腰三角形中,由“一”得“二”.在△ABC中,AB=AC ,∴ BD= CD,AD⊥BC∵ AD是∠BAC的角平分线 (已知),(等腰三角形的三线合一).二、等腰三角形性质ADCB填空:(1)在△ABC中,AB=AC,
∵AD是BC边上的中线(已知),
∴ ,
(等腰三角形的三线合一).(2)在△ABC中,AB=AC,
∵AD是BC边上的高(已知),
∴ ,
( ). AD⊥BC ∠1 =∠2BD=CD ∠1 =∠2等腰三角形的三线合一12课堂练习:
练习册P54--55,1--3三、等腰三角形性质的应用 (1)已知在△ABC中,AB=AC,∠B=70o,
求∠C和∠A的度数。ACB70o分析:等边对等角三角形内角和在等腰三角形中若已知一个内角,即可求出其它内角的大小.如何思考?三、等腰三角形性质的应用 变式1、已知△ABC是等腰三角形,且有一个
内角为70o,那么其他的两个内角的度
数为 。 ACB这类问题需要分类讨论.分析:40o(1)(2)55o55o70o、40o或55o、55o。变式2、把上题中的70o改为100o,会得出什么样的结论?三、等腰三角形性质的应用 (2)如图,已知AB=AC,∠BAC=110°,
AD是△ABC的中线,求∠1和∠2的度数.ABC12D分析:小结:若已知等腰三角形及顶角平分线、底边中线、底边上的高三线之一,可考虑用“等腰三角形三线合一”的性质来说明,而不用三角形全等说明,以简化说理过程.三角形全等等腰三角形的三线合一三、等腰三角形性质的应用 (3)如图,已知AB=AC,AD是BC边上的高,
且DE⊥AB,DF⊥AC,垂足分别是E、F,试
说明BE=CF的理由.分析:课堂练习:书 P107,2课堂小结(3)等腰三角形是轴对称图形,它的对称轴是顶角平分线所在的直线、底边中线所在的直线,也可以说成是底边上的高所在的直线.(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“等腰三角形的三线合一”). 等腰三角形性质(1)等腰三角形的两个底角相等(简称:“等边对等角”).还有什么方法?补充练习:
如图,四边形ABCD的对角线AC与BD相交于点O,AB=AD,
且AC⊥BD,试说明∠1=∠2的理由.分析:
说明∠B=∠C的理由.解:作∠BAC的平分线AD交BC于点D, ∴∠1=∠2(角平分线的意义).在△ABD与△ACD中,AB=AC(已知),
∠1=∠2 (已证),
AD=AD(公共边), ∴△ABD≌△ACD(S.A.S).
∴∠B=∠C(全等三角形的对应角相等).结论:等腰三角形的两个__ 角相等.底在△ABC中,
∵ AB = AC (已知)
∴ ∠B = ∠C(等边对等角)前提!二、等腰三角形性质ADCB12由上面的说理过程中△ABD≌△ACD还可以得到哪些结论? BD=CD AD⊥BC 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“等腰三角形的三线合一”). ∠1=∠2 在等腰三角形中,由“一”得“二”.在△ABC中,AB=AC ,∴ BD= CD,AD⊥BC∵ AD是∠BAC的角平分线 (已知),(等腰三角形的三线合一).二、等腰三角形性质ADCB填空:(1)在△ABC中,AB=AC,
∵AD是BC边上的中线(已知),
∴ ,
(等腰三角形的三线合一).(2)在△ABC中,AB=AC,
∵AD是BC边上的高(已知),
∴ ,
( ). AD⊥BC ∠1 =∠2BD=CD ∠1 =∠2等腰三角形的三线合一12课堂练习:
练习册P54--55,1--3三、等腰三角形性质的应用 (1)已知在△ABC中,AB=AC,∠B=70o,
求∠C和∠A的度数。ACB70o分析:等边对等角三角形内角和在等腰三角形中若已知一个内角,即可求出其它内角的大小.如何思考?三、等腰三角形性质的应用 变式1、已知△ABC是等腰三角形,且有一个
内角为70o,那么其他的两个内角的度
数为 。 ACB这类问题需要分类讨论.分析:40o(1)(2)55o55o70o、40o或55o、55o。变式2、把上题中的70o改为100o,会得出什么样的结论?三、等腰三角形性质的应用 (2)如图,已知AB=AC,∠BAC=110°,
AD是△ABC的中线,求∠1和∠2的度数.ABC12D分析:小结:若已知等腰三角形及顶角平分线、底边中线、底边上的高三线之一,可考虑用“等腰三角形三线合一”的性质来说明,而不用三角形全等说明,以简化说理过程.三角形全等等腰三角形的三线合一三、等腰三角形性质的应用 (3)如图,已知AB=AC,AD是BC边上的高,
且DE⊥AB,DF⊥AC,垂足分别是E、F,试
说明BE=CF的理由.分析:课堂练习:书 P107,2课堂小结(3)等腰三角形是轴对称图形,它的对称轴是顶角平分线所在的直线、底边中线所在的直线,也可以说成是底边上的高所在的直线.(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“等腰三角形的三线合一”). 等腰三角形性质(1)等腰三角形的两个底角相等(简称:“等边对等角”).还有什么方法?补充练习:
如图,四边形ABCD的对角线AC与BD相交于点O,AB=AD,
且AC⊥BD,试说明∠1=∠2的理由.分析:
