14.5 等腰三角形的性质 课件(16张PPT)
文档属性
| 名称 | 14.5 等腰三角形的性质 课件(16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1012.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览


文档简介
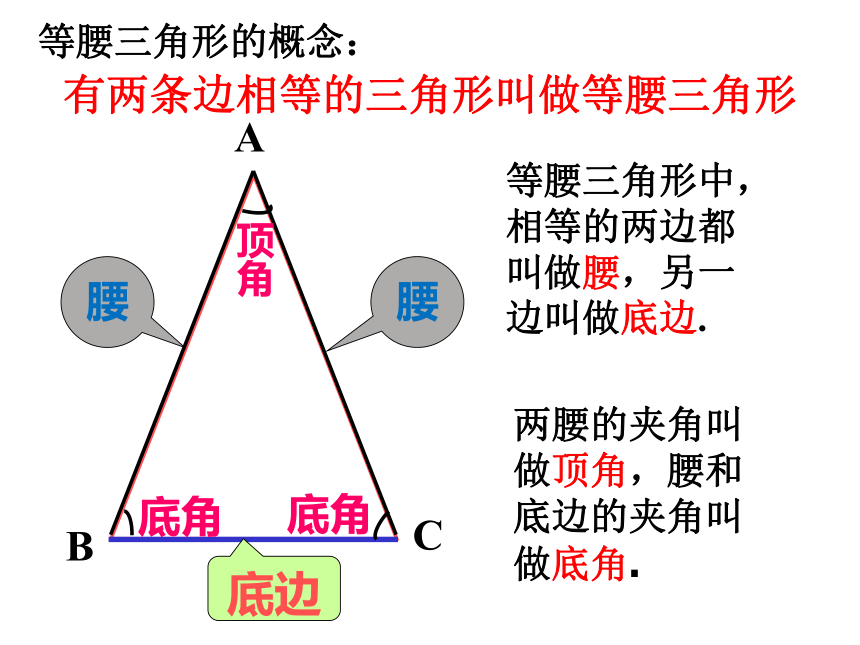
课件16张PPT。从数学的观点去思考,这些图片都含有相同的几何图形吗?等腰三角形的性质等腰三角形中,相等的两边都叫做腰,另一边叫做底边.底边顶角底角底角两腰的夹角叫做顶角,腰和底边的夹角叫做底角.有两条边相等的三角形叫做等腰三角形等腰三角形的概念:已知: △ ABC中,AB=AC.
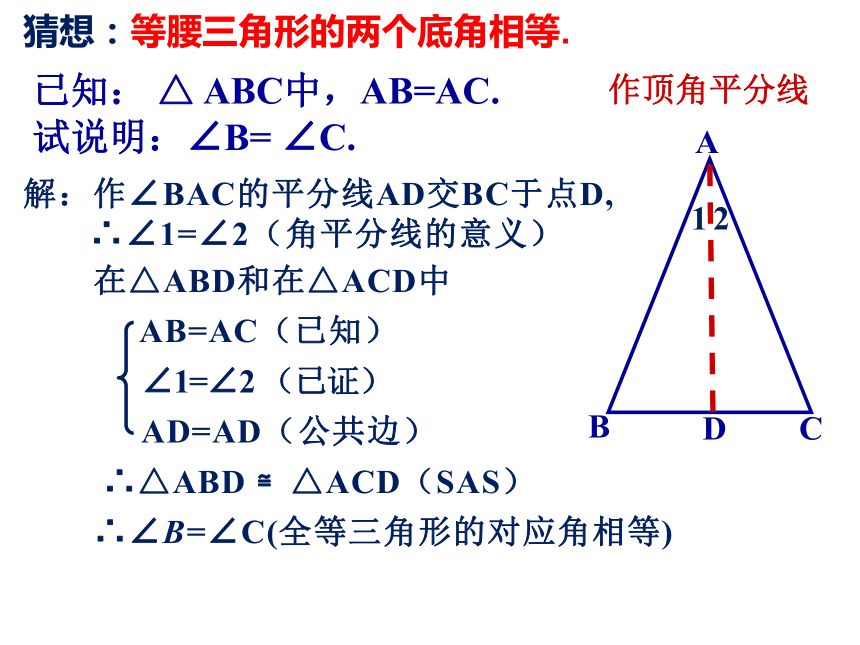
试说明:∠B= ∠C.作顶角平分线猜想:等腰三角形的两个底角相等.解:作∠BAC的平分线AD交BC于点D,
∴∠1=∠2(角平分线的意义)12已知: △ ABC中,AB=AC.
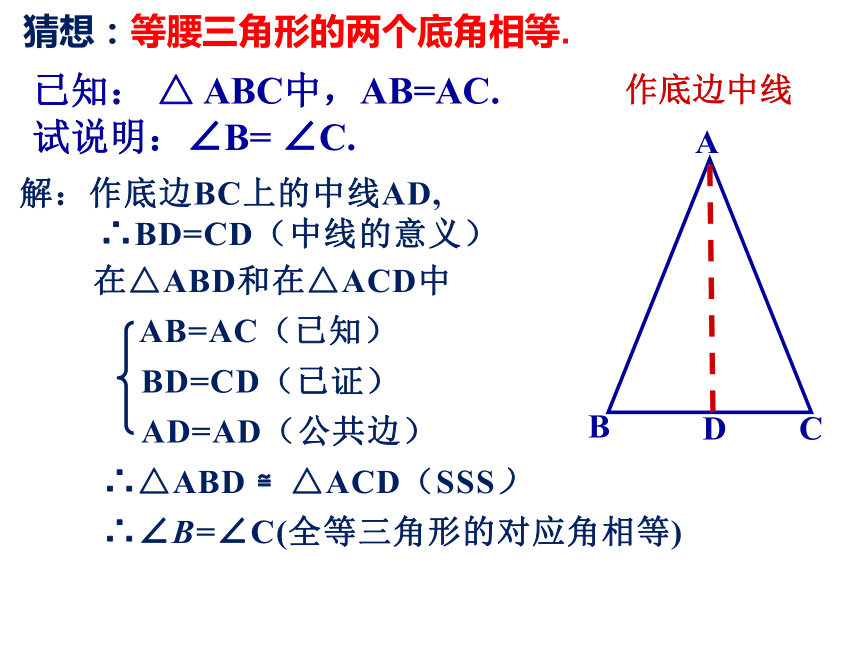
试说明:∠B= ∠C.作底边中线猜想:等腰三角形的两个底角相等.解:作底边BC上的中线AD,
∴BD=CD(中线的意义)注意 等腰三角形性质1:
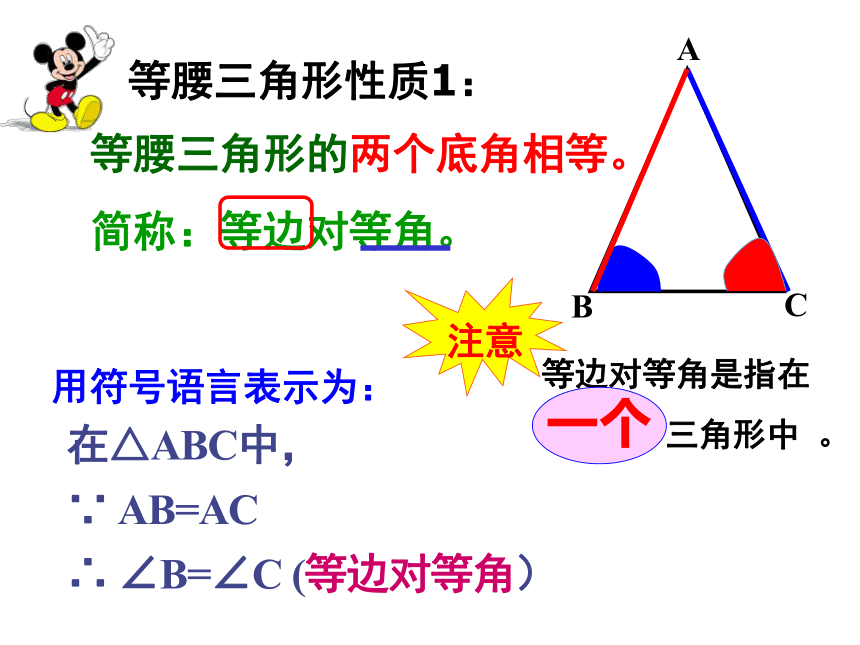
等腰三角形的两个底角相等。
简称:等边对等角。等边对等角是指在
三角形中 。用符号语言表示为:在△ABC中,
∵ AB=AC
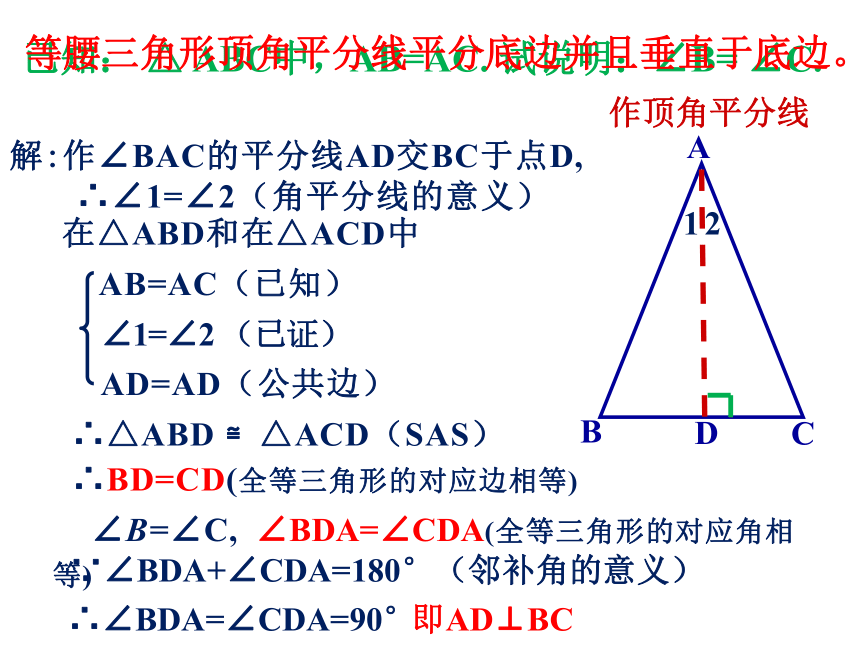
∴ ∠B=∠C (等边对等角)已知: △ ABC中,AB=AC. 试说明:∠B= ∠C.D作顶角平分线解:作∠BAC的平分线AD交BC于点D,
∴∠1=∠2(角平分线的意义)12 ∵∠BDA+∠CDA=180°(邻补角的意义) ∴∠BDA=∠CDA=90°即AD⊥BC ∴BD=CD(全等三角形的对应边相等)
∠B=∠C, ∠BDA=∠CDA(全等三角形的对应角相等)等腰三角形顶角平分线平分底边并且垂直于底边。已知: △ ABC中,AB=AC. 试说明:∠B= ∠C.D作底边中线解:作底边BC上的中线AD,
∴BD=CD(中线的意义)12∵∠BDA+∠CDA=180°(邻补角的意义)
∴∠BDA=∠CDA=90°即AD⊥BC∴∠B=∠C, ∠1=∠2
∠BDA=∠CDA (全等三角形的对应角相等)等腰三角形底边上的中线垂直于底边并且平分顶角已知: △ ABC中,AB=AC. 试说明:∠B= ∠C.作底边上的高 12 BD=CD(全等三角形的对应边相等)∴ ∠1=∠2(全等三角形的对应角相等)等腰三角形底边上的高平分底边和顶角解:过A作AD⊥BC于D
∴ ∠ADB =∠ADC=90°(垂直的意义)∵AB=AC (已知)
∴∠B=∠C(等边对等角) 等腰三角形性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
简称:等腰三角形三线合一等腰三角形 AB=AC① 顶角平分线
② 底边上的中线
③ 底边上的高已知任意一个都可以得其它两个条件.∠1 =∠2,
BD = CD,
AD ⊥ BC
BCDA等腰三角形是轴对称图形,它的对称轴是顶角平分线所在直线,或底边上的中线所在直线,或底边上的高所在的直线. 例1、已知:在△ABC中,AB=AC,∠B=70。,求∠C和∠A的度数.1.等腰三角形一个角为70°,它的另外两个角为_________2.等腰三角形一个角为100°,它的另外两个角为_______40 °,40 °70°, 40°
或55°, 55°解:∵AB=AC , ∠B=70o (已知),
∴∠C=∠B =70°(等边对等角).又∵∠A+∠B+∠C=180o(三角形内角和180o)
∴∠A=180°-70°-70°=40o(等式性质).例2、如图,已知AB=AC,∠BAC=110°
AD是 △ABC的中线,
(1)求∠1和∠2的度数.
(2)AD⊥BC吗?为什么?C例3:如图, 在△ABC 中,AB=AC,
D、E在BC上,AD=AE,你还能找到哪些等量关系?请说明理由。 本节课你学到了什么?小结:(3)等腰三角形是轴对称图形,它的对称轴是顶角平分线所在的直线、底边中线所在的直线,也可以说成是底边上的高所在的直线.(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“等腰三角形的三线合一”). 等腰三角形性质(1)等腰三角形的两个底角相等(简称:“等边对等角”).回家作业(1)完成课后P107练习
(2)完成练习册P54-56 习题14.5
试说明:∠B= ∠C.作顶角平分线猜想:等腰三角形的两个底角相等.解:作∠BAC的平分线AD交BC于点D,
∴∠1=∠2(角平分线的意义)12已知: △ ABC中,AB=AC.
试说明:∠B= ∠C.作底边中线猜想:等腰三角形的两个底角相等.解:作底边BC上的中线AD,
∴BD=CD(中线的意义)注意 等腰三角形性质1:
等腰三角形的两个底角相等。
简称:等边对等角。等边对等角是指在
三角形中 。用符号语言表示为:在△ABC中,
∵ AB=AC
∴ ∠B=∠C (等边对等角)已知: △ ABC中,AB=AC. 试说明:∠B= ∠C.D作顶角平分线解:作∠BAC的平分线AD交BC于点D,
∴∠1=∠2(角平分线的意义)12 ∵∠BDA+∠CDA=180°(邻补角的意义) ∴∠BDA=∠CDA=90°即AD⊥BC ∴BD=CD(全等三角形的对应边相等)
∠B=∠C, ∠BDA=∠CDA(全等三角形的对应角相等)等腰三角形顶角平分线平分底边并且垂直于底边。已知: △ ABC中,AB=AC. 试说明:∠B= ∠C.D作底边中线解:作底边BC上的中线AD,
∴BD=CD(中线的意义)12∵∠BDA+∠CDA=180°(邻补角的意义)
∴∠BDA=∠CDA=90°即AD⊥BC∴∠B=∠C, ∠1=∠2
∠BDA=∠CDA (全等三角形的对应角相等)等腰三角形底边上的中线垂直于底边并且平分顶角已知: △ ABC中,AB=AC. 试说明:∠B= ∠C.作底边上的高 12 BD=CD(全等三角形的对应边相等)∴ ∠1=∠2(全等三角形的对应角相等)等腰三角形底边上的高平分底边和顶角解:过A作AD⊥BC于D
∴ ∠ADB =∠ADC=90°(垂直的意义)∵AB=AC (已知)
∴∠B=∠C(等边对等角) 等腰三角形性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.
简称:等腰三角形三线合一等腰三角形 AB=AC① 顶角平分线
② 底边上的中线
③ 底边上的高已知任意一个都可以得其它两个条件.∠1 =∠2,
BD = CD,
AD ⊥ BC
BCDA等腰三角形是轴对称图形,它的对称轴是顶角平分线所在直线,或底边上的中线所在直线,或底边上的高所在的直线. 例1、已知:在△ABC中,AB=AC,∠B=70。,求∠C和∠A的度数.1.等腰三角形一个角为70°,它的另外两个角为_________2.等腰三角形一个角为100°,它的另外两个角为_______40 °,40 °70°, 40°
或55°, 55°解:∵AB=AC , ∠B=70o (已知),
∴∠C=∠B =70°(等边对等角).又∵∠A+∠B+∠C=180o(三角形内角和180o)
∴∠A=180°-70°-70°=40o(等式性质).例2、如图,已知AB=AC,∠BAC=110°
AD是 △ABC的中线,
(1)求∠1和∠2的度数.
(2)AD⊥BC吗?为什么?C例3:如图, 在△ABC 中,AB=AC,
D、E在BC上,AD=AE,你还能找到哪些等量关系?请说明理由。 本节课你学到了什么?小结:(3)等腰三角形是轴对称图形,它的对称轴是顶角平分线所在的直线、底边中线所在的直线,也可以说成是底边上的高所在的直线.(2)等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“等腰三角形的三线合一”). 等腰三角形性质(1)等腰三角形的两个底角相等(简称:“等边对等角”).回家作业(1)完成课后P107练习
(2)完成练习册P54-56 习题14.5
