14.5 等腰三角形的性质 课件(19张PPT)
文档属性
| 名称 | 14.5 等腰三角形的性质 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 653.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览




文档简介
课件19张PPT。14.5 等腰三角形的性质1、掌握等腰三角形两个底角相等及“三线合一”的性质,能运用等腰三角形的性质解决有关的简单问题.
2、经历观察、猜想、说理等活动,发现并归纳等腰三角形的性质.
3、在探究及运用逻辑推理方法得出等腰三角形性质的过程中,感受几何语言表达的严谨,同时获得探究学习和数学知识应用的体验,感受几何学习的魅力,增强学习兴趣.教学目标:等 腰
三角形 三角形
(按边分类)不等边三角形等腰三角形(等边三角形是特殊的
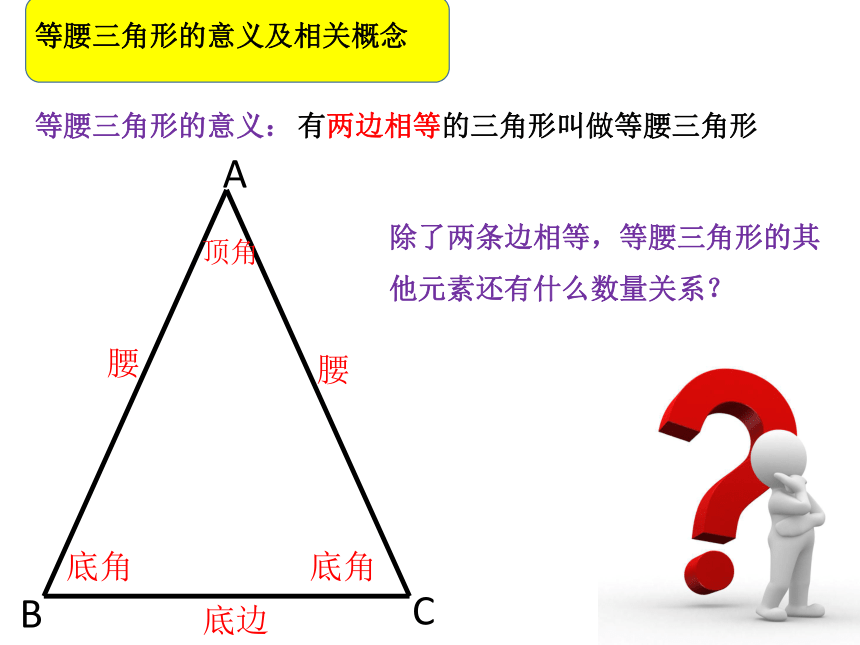
等腰三角形)AC腰腰顶角底角底角底边B等腰三角形的意义及相关概念等腰三角形的意义:有两边相等的三角形叫做等腰三角形除了两条边相等,等腰三角形的其他元素还有什么数量关系?
在△ABC中,AB=AC,说明:∠B = ∠C逻辑推理,证实性质1 在△ABD与△ACD中,
AB=AC(已知)
∠1 = ∠2(已证)
AD=AD(公共边)
∴ △ABD≌ △ACD(SAS)
解:在△ABC中,作∠ BAC的角平分线AD,
与BC交于点D
∴ ∠1 = ∠2(角平分线的意义)
D∴ ∠B = ∠C(全等三角形对应角相等)
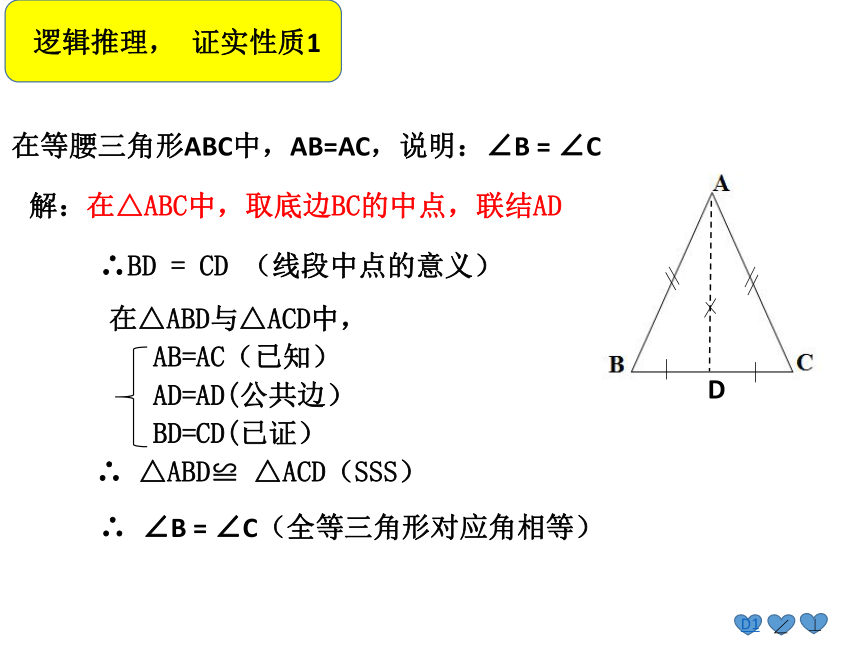
D1中⊥12在等腰三角形ABC中,AB=AC,说明:∠B = ∠C逻辑推理, 证实性质1 在△ABD与△ACD中,
AB=AC(已知)
AD=AD(公共边)
BD=CD(已证)
∴ △ABD≌ △ACD(SSS)
解:在△ABC中,取底边BC的中点,联结AD
∴BD = CD (线段中点的意义)
D∴ ∠B = ∠C(全等三角形对应角相等)
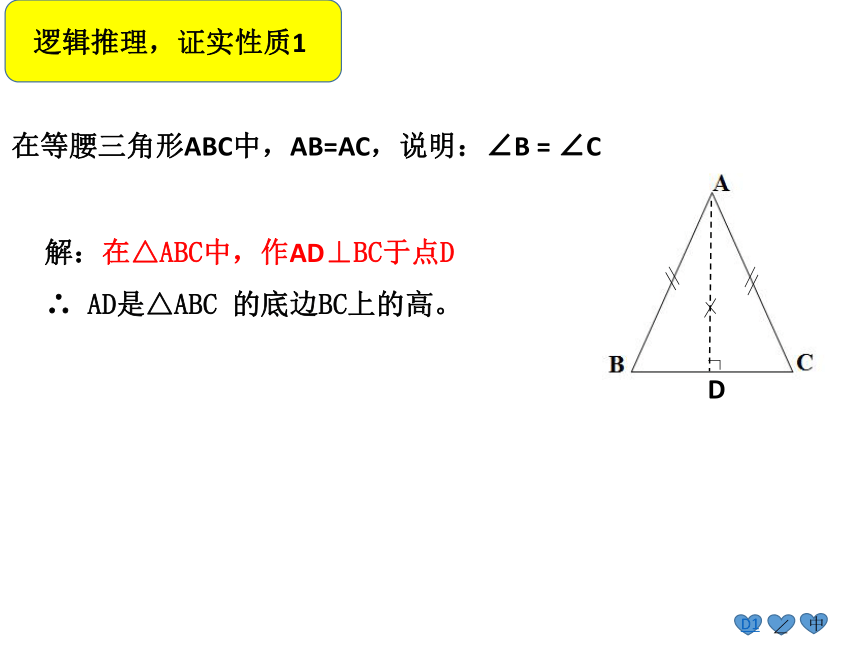
D1⊥∠在等腰三角形ABC中,AB=AC,说明:∠B = ∠C逻辑推理,证实性质1解:在△ABC中,作AD⊥BC于点D
∴ AD是△ABC 的底边BC上的高。
DD1∠中等腰三角形的性质1:等腰三角形的两个底角相等(简称“等边对等角”)。符号语言:
在△ABC中,AB=AC,
∴∠B = ∠C(等边对等角)
性质运用,巩固新知基础练习:
(1)如图,△ABC中,AB=AC,∠B=70°,
则∠C= ,∠A= 。
(2) 等腰三角形ABC中,如果有一个内角是70°,则
其他两个内角的度数为 70°40° 70°、40° 55°、55° 或(3) 等腰三角形ABC中,如果有一个内角是100°,则
其他两个内角的度数为 40°、40° 逻辑推理,证实性质2 在△ABD与△ACD中,
AB=AC(已知)
∠1= ∠2(已证)
AD=AD(公共边)
∴ △ABD ≌ △ACD(SAS)
解:在△ABC中,作∠ BAC的角平分线AD,
与BC交于点D
∴ ∠1 = ∠2(角平分线的意义)
D∴ ∠B = ∠C(全等三角形对应角相等)
从中还可以得到哪些相等的边和相等的角?在等腰三角形ABC中,AB=AC,说明:∠B = ∠C∠中⊥D212在等腰三角形ABC中,AB=AC,说明:∠B = ∠C逻辑推理,证实性质2 在△ABD与△ACD中,
AB=AC(已知)
∠1 = ∠2(已证)
AD=AD(公共边)
∴ △ABD≌ △ACD(SAS)
∴ ∠1 = ∠2 (角平分线的意义)
D∴ ∠B = ∠C(全等三角形对应角相等)
BD = CD(全等三角形对应边相等)
又∵ ∠BDA + ∠CDA=180°(邻补角的意义)
∴ 2 ∠BDA =180°(等量代换)
∴∠BDA =90°(等式性质)
∴ AD⊥BC(垂直的意义)
AD ⊥ BC∴BD = CD 解:在△ABC中,作∠ BAC的角平分线AD,交BC于点D
∠BDA = ∠CDA (全等三角形对应角相等)
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。在△ABC中,
∵ AB=AC,∠1=∠2∴ BD=CD , AD⊥BC D2中⊥12在等腰三角形ABC中,AB=AC,说明:∠B = ∠C逻辑推理,证实性质2解:在△ABC中,取底边BC的中点D,联结AD
∴BD = CD (线段中点的意义)
∴线段AD是△ABC 的底边BC上的中线。
在△ABD与△ACD中,
AB=AC(已知)
AD=AD(公共边)
BD=CD(已证)
∴ △ABD≌ △ACD(SSS)
∴ ∠B = ∠C(全等三角形对应角相等)
∠1= ∠2 AD ⊥ BC∴∠1 = ∠2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。 在△ABC中,
∵ AB=AC ,BD=CD∠1 = ∠2 ,AD⊥BC
又∵ ∠BDA + ∠CDA=180°(邻补角的意义)
∴ 2 ∠BDA =180°(等量代换)
∴∠BDA =90°(等式性质)
∴ AD⊥BC(垂直的意义)
∠BDA = ∠CDA (全等三角形对应角相等)
D2⊥∠12在等腰三角形ABC中,AB=AC,说明:∠B = ∠C解:在△ABC中,作BC上的高AD
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合在△ABC中,
∵ AB=AC,AD⊥BC ∴ BD=CD , ∠1=∠2
D2中∠D12等腰三角形的性质2:等腰三角形形的顶角平分线、底边上的中线、底边上的高互相重合。(简称“等腰三角形的三线合一”)。符号语言: 在△ABC中,
∵AB=AC,BD=CD∴∠1=∠2 AD⊥BC ∵ AB=AC, ∠1=∠2∴ BD=CD AD⊥BC ∵ AB=AC, AD⊥BC ∴ BD=CD ∠1=∠212等腰三角形的性质3:等腰三角形是 图形。它的对称轴是顶角的平分线所在的直线底边上的中线所在的直线或底边上的高所在的直线或底边上的中垂线或轴对称例1:如图,已知AB=AC,∠BAC=110°,AD是△ABC的中线,(1)求∠1和∠2的度数。
(2)AD⊥BC吗?为什么?性质运用,巩固新知XJ例1:如图,已知AB=AC,∠BAC=110°,AD是△ABC的中线,(1)求∠1和∠2的度数。
(2)AD⊥BC吗?为什么?性质运用,巩固新知?(2)在△ABC中,AB=AC(已知)
∵ AD是△ABC的中线(已知)
∴ AD⊥BC(等腰三角形的三线合一)归纳小结1、这节课你学到了什么?2、你还想继续学习什么?巩固提升练习:
如图,△ABC中,AB=AC,BE=CE,延长AE交BC于点D,
试说明 AD⊥BC 的理由。
2、经历观察、猜想、说理等活动,发现并归纳等腰三角形的性质.
3、在探究及运用逻辑推理方法得出等腰三角形性质的过程中,感受几何语言表达的严谨,同时获得探究学习和数学知识应用的体验,感受几何学习的魅力,增强学习兴趣.教学目标:等 腰
三角形 三角形
(按边分类)不等边三角形等腰三角形(等边三角形是特殊的
等腰三角形)AC腰腰顶角底角底角底边B等腰三角形的意义及相关概念等腰三角形的意义:有两边相等的三角形叫做等腰三角形除了两条边相等,等腰三角形的其他元素还有什么数量关系?
在△ABC中,AB=AC,说明:∠B = ∠C逻辑推理,证实性质1 在△ABD与△ACD中,
AB=AC(已知)
∠1 = ∠2(已证)
AD=AD(公共边)
∴ △ABD≌ △ACD(SAS)
解:在△ABC中,作∠ BAC的角平分线AD,
与BC交于点D
∴ ∠1 = ∠2(角平分线的意义)
D∴ ∠B = ∠C(全等三角形对应角相等)
D1中⊥12在等腰三角形ABC中,AB=AC,说明:∠B = ∠C逻辑推理, 证实性质1 在△ABD与△ACD中,
AB=AC(已知)
AD=AD(公共边)
BD=CD(已证)
∴ △ABD≌ △ACD(SSS)
解:在△ABC中,取底边BC的中点,联结AD
∴BD = CD (线段中点的意义)
D∴ ∠B = ∠C(全等三角形对应角相等)
D1⊥∠在等腰三角形ABC中,AB=AC,说明:∠B = ∠C逻辑推理,证实性质1解:在△ABC中,作AD⊥BC于点D
∴ AD是△ABC 的底边BC上的高。
DD1∠中等腰三角形的性质1:等腰三角形的两个底角相等(简称“等边对等角”)。符号语言:
在△ABC中,AB=AC,
∴∠B = ∠C(等边对等角)
性质运用,巩固新知基础练习:
(1)如图,△ABC中,AB=AC,∠B=70°,
则∠C= ,∠A= 。
(2) 等腰三角形ABC中,如果有一个内角是70°,则
其他两个内角的度数为 70°40° 70°、40° 55°、55° 或(3) 等腰三角形ABC中,如果有一个内角是100°,则
其他两个内角的度数为 40°、40° 逻辑推理,证实性质2 在△ABD与△ACD中,
AB=AC(已知)
∠1= ∠2(已证)
AD=AD(公共边)
∴ △ABD ≌ △ACD(SAS)
解:在△ABC中,作∠ BAC的角平分线AD,
与BC交于点D
∴ ∠1 = ∠2(角平分线的意义)
D∴ ∠B = ∠C(全等三角形对应角相等)
从中还可以得到哪些相等的边和相等的角?在等腰三角形ABC中,AB=AC,说明:∠B = ∠C∠中⊥D212在等腰三角形ABC中,AB=AC,说明:∠B = ∠C逻辑推理,证实性质2 在△ABD与△ACD中,
AB=AC(已知)
∠1 = ∠2(已证)
AD=AD(公共边)
∴ △ABD≌ △ACD(SAS)
∴ ∠1 = ∠2 (角平分线的意义)
D∴ ∠B = ∠C(全等三角形对应角相等)
BD = CD(全等三角形对应边相等)
又∵ ∠BDA + ∠CDA=180°(邻补角的意义)
∴ 2 ∠BDA =180°(等量代换)
∴∠BDA =90°(等式性质)
∴ AD⊥BC(垂直的意义)
AD ⊥ BC∴BD = CD 解:在△ABC中,作∠ BAC的角平分线AD,交BC于点D
∠BDA = ∠CDA (全等三角形对应角相等)
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。在△ABC中,
∵ AB=AC,∠1=∠2∴ BD=CD , AD⊥BC D2中⊥12在等腰三角形ABC中,AB=AC,说明:∠B = ∠C逻辑推理,证实性质2解:在△ABC中,取底边BC的中点D,联结AD
∴BD = CD (线段中点的意义)
∴线段AD是△ABC 的底边BC上的中线。
在△ABD与△ACD中,
AB=AC(已知)
AD=AD(公共边)
BD=CD(已证)
∴ △ABD≌ △ACD(SSS)
∴ ∠B = ∠C(全等三角形对应角相等)
∠1= ∠2 AD ⊥ BC∴∠1 = ∠2 等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。 在△ABC中,
∵ AB=AC ,BD=CD∠1 = ∠2 ,AD⊥BC
又∵ ∠BDA + ∠CDA=180°(邻补角的意义)
∴ 2 ∠BDA =180°(等量代换)
∴∠BDA =90°(等式性质)
∴ AD⊥BC(垂直的意义)
∠BDA = ∠CDA (全等三角形对应角相等)
D2⊥∠12在等腰三角形ABC中,AB=AC,说明:∠B = ∠C解:在△ABC中,作BC上的高AD
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合在△ABC中,
∵ AB=AC,AD⊥BC ∴ BD=CD , ∠1=∠2
D2中∠D12等腰三角形的性质2:等腰三角形形的顶角平分线、底边上的中线、底边上的高互相重合。(简称“等腰三角形的三线合一”)。符号语言: 在△ABC中,
∵AB=AC,BD=CD∴∠1=∠2 AD⊥BC ∵ AB=AC, ∠1=∠2∴ BD=CD AD⊥BC ∵ AB=AC, AD⊥BC ∴ BD=CD ∠1=∠212等腰三角形的性质3:等腰三角形是 图形。它的对称轴是顶角的平分线所在的直线底边上的中线所在的直线或底边上的高所在的直线或底边上的中垂线或轴对称例1:如图,已知AB=AC,∠BAC=110°,AD是△ABC的中线,(1)求∠1和∠2的度数。
(2)AD⊥BC吗?为什么?性质运用,巩固新知XJ例1:如图,已知AB=AC,∠BAC=110°,AD是△ABC的中线,(1)求∠1和∠2的度数。
(2)AD⊥BC吗?为什么?性质运用,巩固新知?(2)在△ABC中,AB=AC(已知)
∵ AD是△ABC的中线(已知)
∴ AD⊥BC(等腰三角形的三线合一)归纳小结1、这节课你学到了什么?2、你还想继续学习什么?巩固提升练习:
如图,△ABC中,AB=AC,BE=CE,延长AE交BC于点D,
试说明 AD⊥BC 的理由。
