14.4(4)全等三角形的判定 课件(17张PPT)
文档属性
| 名称 | 14.4(4)全等三角形的判定 课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览



文档简介
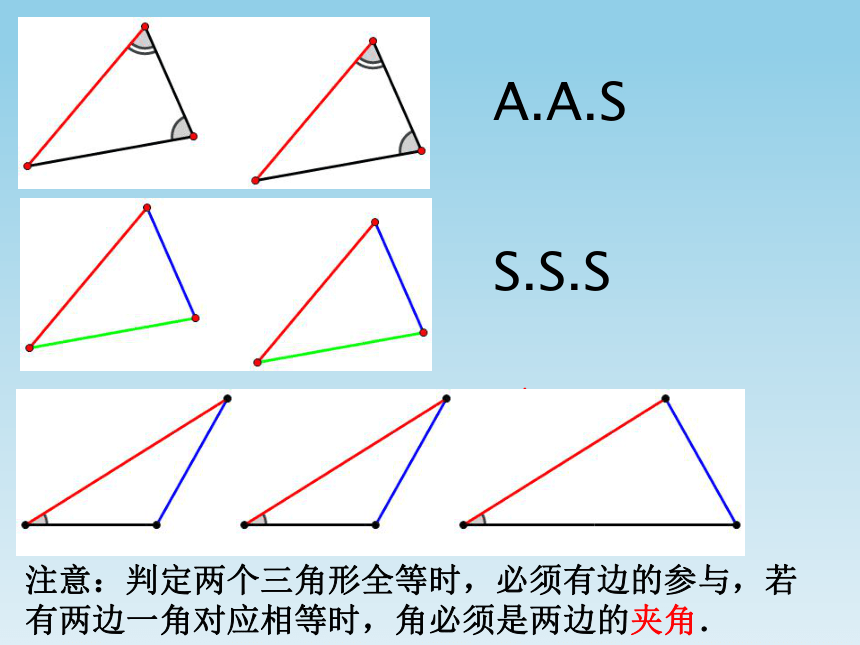
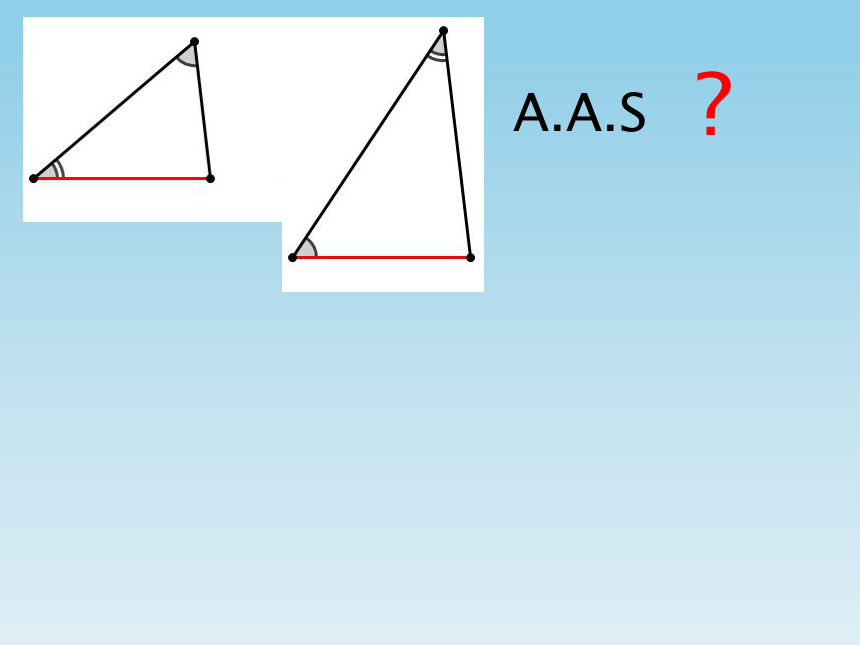
课件17张PPT。14.4(4)全等三角形的判定??S.A.SA.S.AA.A.SS.S.SS.S.A注意:判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.A.A.S?典型例题分析:
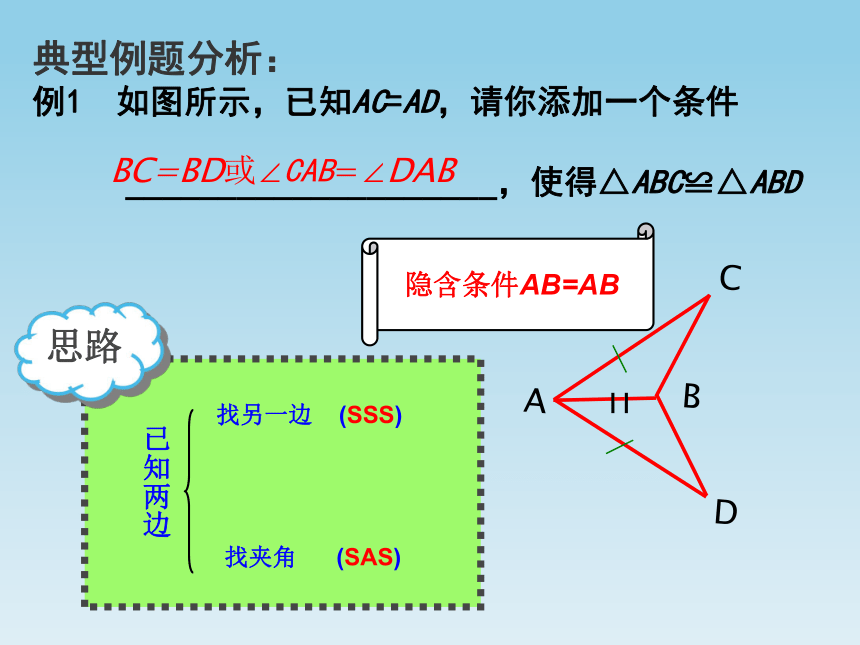
例1 如图所示,已知AC=AD,请你添加一个条件
____________________,使得△ABC≌△ABD思路隐含条件AB=ABBC=BD或∠CAB=∠DAB变式1:如图,已知∠C=∠D,请你添加一个条件
____________________,使得 △ABC≌△ABD思路隐含条件AB=AB 已知一边一角
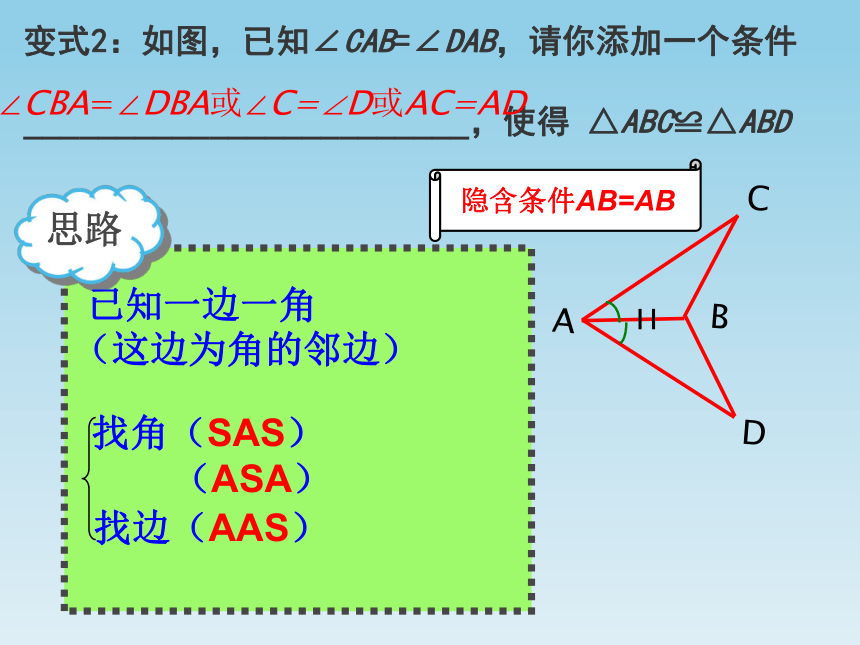
(这边为角的对边)找任一角(AAS)∠CBA=∠DBA或∠CAB=∠DAB变式2:如图,已知∠CAB=∠DAB,请你添加一个条件
________________________,使得 △ABC≌△ABD思路隐含条件AB=AB已知一边一角(这边为角的邻边)∠CBA=∠DBA或∠C=∠D或AC=AD变式3、如图所示:已知∠B=∠C,请你添加一个条件
_______________________,使得△ABE≌△ACD思路隐含条件∠A为公共角AB=AC或AD=AE或BE=CD变式4 如图,已知AB=AC,请你添加一个条件
______________,说明ΔBOE ≌ ΔCOD. 典型例题分析:
例2 在△AFD中和△CEB中,点A、E、F、C在同一条直线上,有下面四个等量关系:
① AD=CB; ② AE=CF; ③ ∠B=∠D; ④ AD//BC
请用其中的3个作为条件,余下的一个作为结论,编写一道几何题,并加以证明.?①∠D=∠C,∠BAD= ∠ABC
② ∠BAD= ∠ABC , ∠ABD= ∠BAC
③BD=AC, ∠BAD= ∠ABC
④AD=BC,BD=AC练习1 ③练习2 如图,已知∠1=∠2,AC=AD,添加一个条件件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1B练习3 已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( )
A.1对 B.2对
C.3对 D.4对 D练习4 如图,给出五个等量关系:
①AD=BC ②AC=BD ③CE=DE ④∠D=∠C
⑤∠DAB=∠CBA.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.课堂小结:这堂课你有什么收获?布置作业:一课一练14.4(4)拓展1 在△ ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
求证:DE=AD+BE拓展2 在△ABC中, ∠B=2∠C, AD平分∠BAC.
求证:AB+BD=ACABCDABCD
例1 如图所示,已知AC=AD,请你添加一个条件
____________________,使得△ABC≌△ABD思路隐含条件AB=ABBC=BD或∠CAB=∠DAB变式1:如图,已知∠C=∠D,请你添加一个条件
____________________,使得 △ABC≌△ABD思路隐含条件AB=AB 已知一边一角
(这边为角的对边)找任一角(AAS)∠CBA=∠DBA或∠CAB=∠DAB变式2:如图,已知∠CAB=∠DAB,请你添加一个条件
________________________,使得 △ABC≌△ABD思路隐含条件AB=AB已知一边一角(这边为角的邻边)∠CBA=∠DBA或∠C=∠D或AC=AD变式3、如图所示:已知∠B=∠C,请你添加一个条件
_______________________,使得△ABE≌△ACD思路隐含条件∠A为公共角AB=AC或AD=AE或BE=CD变式4 如图,已知AB=AC,请你添加一个条件
______________,说明ΔBOE ≌ ΔCOD. 典型例题分析:
例2 在△AFD中和△CEB中,点A、E、F、C在同一条直线上,有下面四个等量关系:
① AD=CB; ② AE=CF; ③ ∠B=∠D; ④ AD//BC
请用其中的3个作为条件,余下的一个作为结论,编写一道几何题,并加以证明.?①∠D=∠C,∠BAD= ∠ABC
② ∠BAD= ∠ABC , ∠ABD= ∠BAC
③BD=AC, ∠BAD= ∠ABC
④AD=BC,BD=AC练习1 ③练习2 如图,已知∠1=∠2,AC=AD,添加一个条件件:①AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使ΔABC≌ΔAED的条件有( )个. A.4 B.3 C.2 D.1B练习3 已知:如图,CD⊥AB,BE⊥AC,垂足分别为D、E,BE、CD相交于O点,∠1=∠2,图中全等的三角形共有( )
A.1对 B.2对
C.3对 D.4对 D练习4 如图,给出五个等量关系:
①AD=BC ②AC=BD ③CE=DE ④∠D=∠C
⑤∠DAB=∠CBA.请你以其中两个为条件,另三个中的一个为结论,推出一个正确的结论(只需写出一种情况),并加以证明.课堂小结:这堂课你有什么收获?布置作业:一课一练14.4(4)拓展1 在△ ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
求证:DE=AD+BE拓展2 在△ABC中, ∠B=2∠C, AD平分∠BAC.
求证:AB+BD=ACABCDABCD
