14.4(2) 全等三角形的判定 课件(17张PPT)
文档属性
| 名称 | 14.4(2) 全等三角形的判定 课件(17张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 17:35:56 | ||
图片预览



文档简介
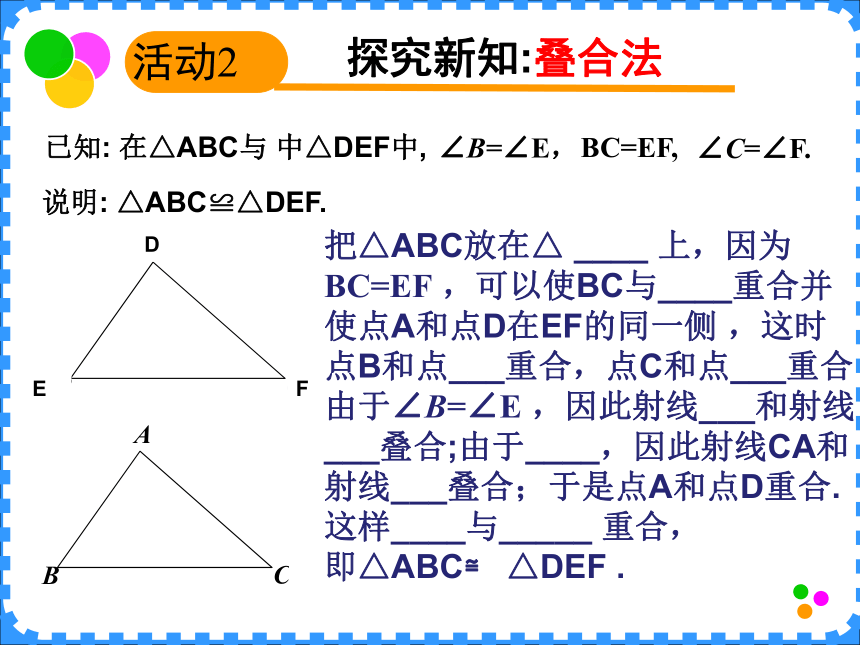
课件17张PPT。§14.4(2)全等三角形的判定七年级下册第十四章 三角形名字:泰勒斯国籍:古希腊头衔:思想家哲学家科学家数学家主要成就:希腊七贤之一哲学和科学的始祖命题证明探究新知:叠合法活动2 已知: 在△ABC与 中△DEF中, 说明: △ABC≌△DEF.∠B=∠E,BC=EF,∠C=∠F.把△ABC放在△ ____ 上,因为BC=EF ,可以使BC与____重合并使点A和点D在EF的同一侧 ,这时点B和点___重合,点C和点___重合由于∠B=∠E ,因此射线___和射线___叠合;由于____,因此射线CA和射线___叠合;于是点A和点D重合. 这样____与_____ 重合,
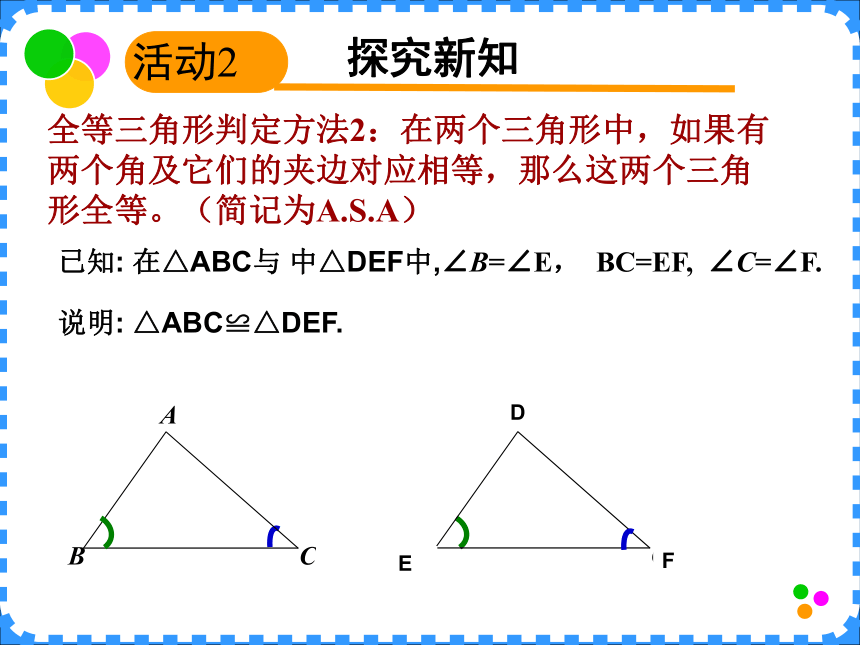
即△ABC≌ △DEF .【古希腊】欧几里得 探究新知活动2 全等三角形判定方法2:在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等。(简记为A.S.A)已知: 在△ABC与 中△DEF中,∠B=∠E, BC=EF, ∠C=∠F.DEF说明: △ABC≌△DEF.探究新知活动2 全等三角形判定方法3:在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等。(简记为A.A.S )已知: 在△ABC与 中△DEF中,∠A=∠D,∠C=∠F ,BC=EF.DEF说明: △ABC≌△DEF.新知应用活动3 练习1 判定下列各对三角形是否全等,如果全等,请说出理由。( )( )( )( )新知应用活动3 例题1 如图,已知AB与CD相交于点O,AO=BO, ∠A=∠B, 说明△AOC与△BOD全等的理由.解:在△AOC与△BOD中∠A=∠B(已知)AO=BO(已知)∠AOC=∠BOD(对顶角相等)?新知应用活动3 例题2 如图,已知AE=AC, ∠B=∠D,说明△DEA与△BCA全等的理由。解:AED新知应用活动3 例题2 如图,已知AE=AC, ∠B=∠D,说明△DEA与△BCA全等的理由。解:在△ABC与△ADE中∠B=∠D(已知)∠BAC=∠DAE(公共角)AC=AE(已知)∴△ABC≌△ADE(A.A.S)巩固新知活动4 练习 如图,∠1=∠2,AD=AE, ∠B=∠ACE,且B,C,D三点在一直线上,试说明BD与CE相等的理由。解:21巩固新知活动4 练习 如图,∠1=∠2,AD=AE, ∠B=∠ACE,且B,C,D三点在一直线上,试说明BD与CE相等的理由。解:21自主小结活动5 通过了今天的学习
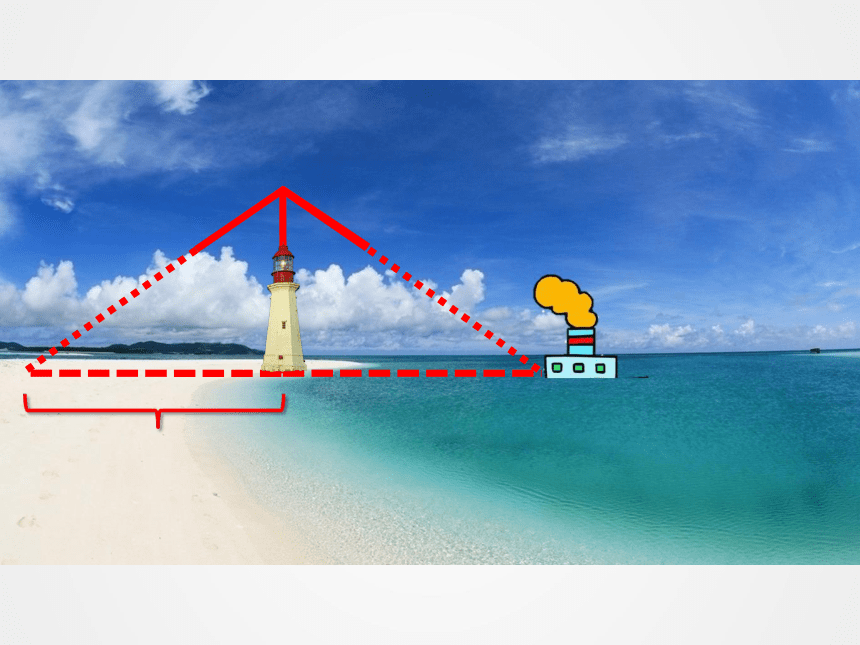
你有什么收获吗?拓展延伸活动4 学校门口有一条美丽的苏州河,你能测量一下河宽吗?
即△ABC≌ △DEF .【古希腊】欧几里得 探究新知活动2 全等三角形判定方法2:在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等。(简记为A.S.A)已知: 在△ABC与 中△DEF中,∠B=∠E, BC=EF, ∠C=∠F.DEF说明: △ABC≌△DEF.探究新知活动2 全等三角形判定方法3:在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等。(简记为A.A.S )已知: 在△ABC与 中△DEF中,∠A=∠D,∠C=∠F ,BC=EF.DEF说明: △ABC≌△DEF.新知应用活动3 练习1 判定下列各对三角形是否全等,如果全等,请说出理由。( )( )( )( )新知应用活动3 例题1 如图,已知AB与CD相交于点O,AO=BO, ∠A=∠B, 说明△AOC与△BOD全等的理由.解:在△AOC与△BOD中∠A=∠B(已知)AO=BO(已知)∠AOC=∠BOD(对顶角相等)?新知应用活动3 例题2 如图,已知AE=AC, ∠B=∠D,说明△DEA与△BCA全等的理由。解:AED新知应用活动3 例题2 如图,已知AE=AC, ∠B=∠D,说明△DEA与△BCA全等的理由。解:在△ABC与△ADE中∠B=∠D(已知)∠BAC=∠DAE(公共角)AC=AE(已知)∴△ABC≌△ADE(A.A.S)巩固新知活动4 练习 如图,∠1=∠2,AD=AE, ∠B=∠ACE,且B,C,D三点在一直线上,试说明BD与CE相等的理由。解:21巩固新知活动4 练习 如图,∠1=∠2,AD=AE, ∠B=∠ACE,且B,C,D三点在一直线上,试说明BD与CE相等的理由。解:21自主小结活动5 通过了今天的学习
你有什么收获吗?拓展延伸活动4 学校门口有一条美丽的苏州河,你能测量一下河宽吗?
