14.4(1) 全等三角形的判定 课件(18张)
文档属性
| 名称 | 14.4(1) 全等三角形的判定 课件(18张) |  | |
| 格式 | zip | ||
| 文件大小 | 441.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 17:35:56 | ||
图片预览






文档简介
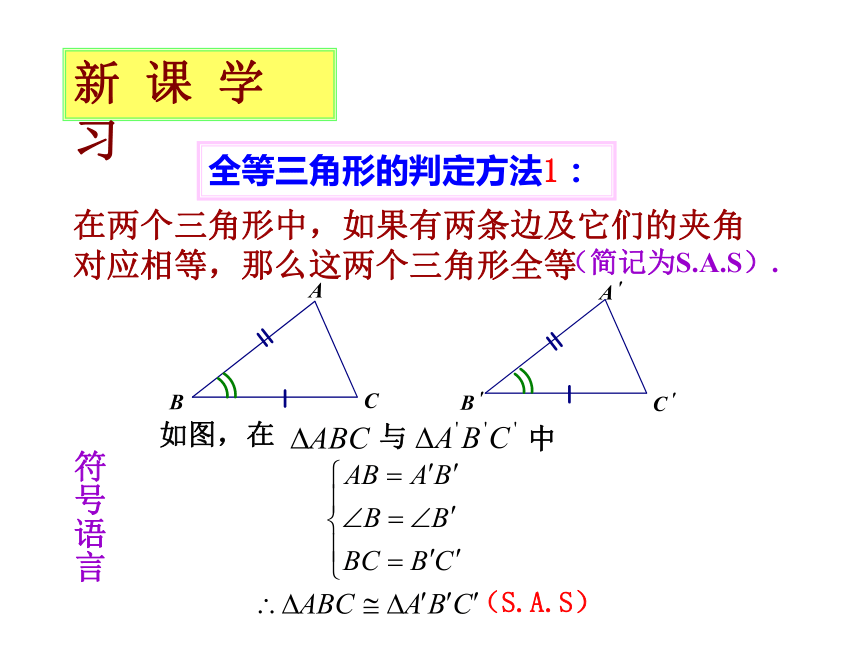
课件18张PPT。14.4 全等三角形的判定(1) 复 习 引 入 给出三个怎样的元素就能画出三角形呢?(1)“三边”(2)“两边及其夹角”(3)“两角及其夹边”(4)“两角及其中一角的对边” 作 业 回 顾课本P91,1、2、3、41.画⊿ABC,使AB=5cm, BC=4cm, AC=6cm.2.画⊿ABC,使AB=4cm,AC=3cm, ∠A=45°.(三边)(两边及其夹角)按照这样的三个条件画出的三角形都互相重合 作 业 回 顾3.画△ABC,使∠A=40°, ∠B=45°, AB=4cm.4.画△ABC,使∠A=45°, ∠B=60°, AC=3cm.(两角及其夹边)(两角及其中一角的对边)按照这样的三个条件画出的三角形都互相重合 作 业 回 顾一个三角形的形状和大小可以由这个三角形的“三边”或“两边及其夹角”或“两角及其夹边”或“两角及其中一角的对边”确定哪些元素确定?若两个三角形满足所述的三个条件,则它们就是全等三角形新 课 学 习全等三角形的判定方法1: 在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等 (简记为S.A.S).(S.A.S)符号语言新 课 学 习全等三角形的判定方法2 :在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为A.S.A).(A.S.A)符号语言新 课 学 习全等三角形的判定方法3 :在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等 (简记为A.A.S).(A.A.S)符号语言A.A.S和A.S.A有什么区别?三角形的三条边固定了,这个三角形的大小和形状就确定了新 课 学 习全等三角形的判定方法4 :在两个三角形中,如果有三条边对应相等,那么这两个三角形 (简记为S.S.S).(S.S.S)符号语言三角形的稳定性⊿ABC与⊿DEF全等吗?“边边角”(S.S.A),“角角角”(A.A.A)能不能判定出两个三角形全等呢?新 课 学 习思考:DS.S.A不能判定全等A.A.A不能判定全等⊿ABC与⊿ABD具备什么条件?全等吗?与 不全等与 不全等 适 时 小 结1、全等三角形的四个判定方法(S.A.S)(A.S.A)(A.A.S)(S.S.S)2、A.A.A、S.S.A 不能判定两个三角形全等边角边角边角角角边边边边新 课 学 习例1、判断下列各对三角形是否全等,如果全等,请说出理由 解:(1)全等S.A.S (2)全等A.S.A (3)全等A.A.S (4)不全等(5)不全等(6)全等S.S.S 例2、找出图中的全等三角形,并说明它们全等的理由 新 课 学 习(1)和(7)全等 S.A.S (2)和(8)全等 A.S.A (4)和(10)全等 S.S.S (5)和(6)全等 A.A.S 解: 课 堂 练 习1. 两个三角形中,已知___________________________________对应相等,则可依据A.S.A 判定这两个三角形全等.
2. 两个三角形中,已知___________________________________对应相等,则可依据A.A.S 判定这两个三角形全等.
3. 两个三角形中,已知___________________________________对应相等,则可依据S.A.S 判定这两个三角形全等.
4. 两个三角形中,已知___________________________________对应相等,则可依据S.S.S判定这两个三角形全等.一. 填空有两条边及它们的夹角有两个角及它们的夹边有两个角及其中一个角的对边有三条边 课 堂 练 习5、课本:
P.93 / 1, 2
P.96 / 1, 3
P.98 / 1课 堂 练 习6、如图(1)若AB=DF,AC=DE,可添加什么条件得到△ABC≌△DFE,依据是什么? (2)若∠A=∠D,∠C=∠E,可添加什么条件得出△ABC≌△DFE,依据是什么? 解:(1)添加 ∠A=∠D,依据 S.A.S (2)添加 AC=DE,依据 A.S.A 添加 BC=FE,或 添加 AB=DF,依据 A.A.S 依据 A.A.S 或 添加 BC=FE,或依据 S.S.S 正确选择判定方法课 堂 小 结本节课主要学习了什么?你有何收获? 1、全等三角形的四个判定方法及其表示 (S.A.S)(A.S.A)(A.A.S)(S.S.S)2、A.A.A、S.S.A 不能用来判定两个三角形全等. 3、选择正确判定方法判定两个三角形全等. 布 置 作 业1、见作业卷
2、熟记全等三角形的四个判定方法及符号表示
2. 两个三角形中,已知___________________________________对应相等,则可依据A.A.S 判定这两个三角形全等.
3. 两个三角形中,已知___________________________________对应相等,则可依据S.A.S 判定这两个三角形全等.
4. 两个三角形中,已知___________________________________对应相等,则可依据S.S.S判定这两个三角形全等.一. 填空有两条边及它们的夹角有两个角及它们的夹边有两个角及其中一个角的对边有三条边 课 堂 练 习5、课本:
P.93 / 1, 2
P.96 / 1, 3
P.98 / 1课 堂 练 习6、如图(1)若AB=DF,AC=DE,可添加什么条件得到△ABC≌△DFE,依据是什么? (2)若∠A=∠D,∠C=∠E,可添加什么条件得出△ABC≌△DFE,依据是什么? 解:(1)添加 ∠A=∠D,依据 S.A.S (2)添加 AC=DE,依据 A.S.A 添加 BC=FE,或 添加 AB=DF,依据 A.A.S 依据 A.A.S 或 添加 BC=FE,或依据 S.S.S 正确选择判定方法课 堂 小 结本节课主要学习了什么?你有何收获? 1、全等三角形的四个判定方法及其表示 (S.A.S)(A.S.A)(A.A.S)(S.S.S)2、A.A.A、S.S.A 不能用来判定两个三角形全等. 3、选择正确判定方法判定两个三角形全等. 布 置 作 业1、见作业卷
2、熟记全等三角形的四个判定方法及符号表示
