14.5 等腰三角形的性质 课件(25张PPT)
文档属性
| 名称 | 14.5 等腰三角形的性质 课件(25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 991.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览



文档简介
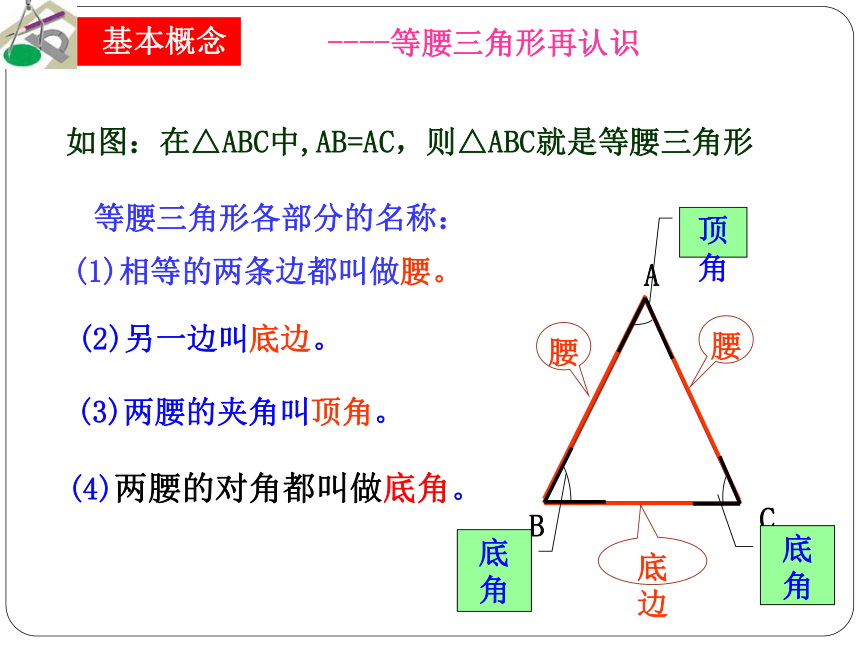
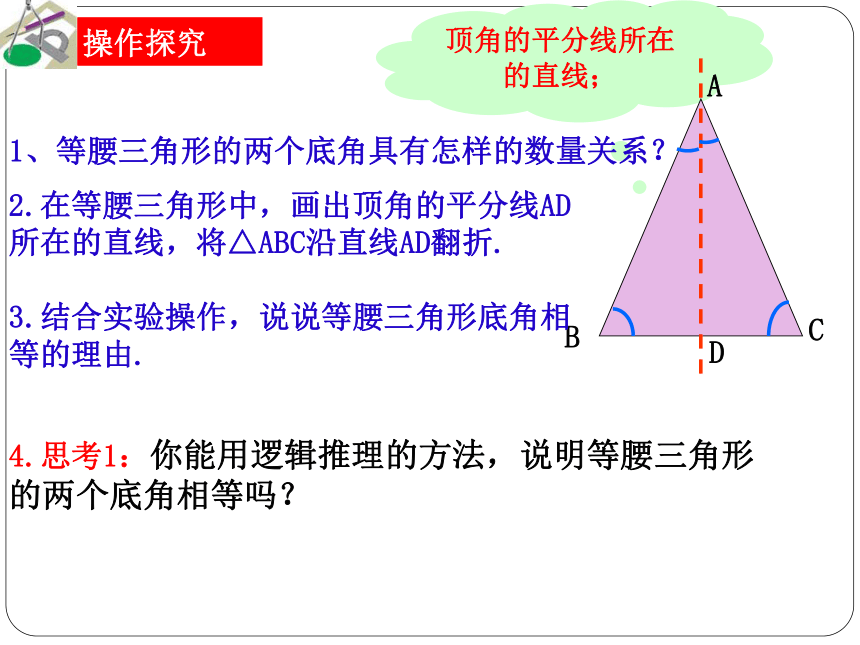
课件28张PPT。下载图片共同特点?生活中的几何图形 它们都是……在你的印象中,什么样的三角形叫做等腰三角形? 有两条边相等的三角形叫做等腰三角形 思考 14.5 等腰三角形的性质如图:在△ABC中,AB=AC,则△ABC就是等腰三角形等腰三角形各部分的名称:(1)相等的两条边都叫做腰。(2)另一边叫底边。(3)两腰的夹角叫顶角。(4)两腰的对角都叫做底角。----等腰三角形再认识顶角的平分线所在的直线; ABCD1、等腰三角形的两个底角具有怎样的数量关系?2.在等腰三角形中,画出顶角的平分线AD所在的直线,将△ABC沿直线AD翻折.
3.结合实验操作,说说等腰三角形底角相等的理由. 操作与思考 操作探究4.思考1:你能用逻辑推理的方法,说明等腰三角形的两个底角相等吗?
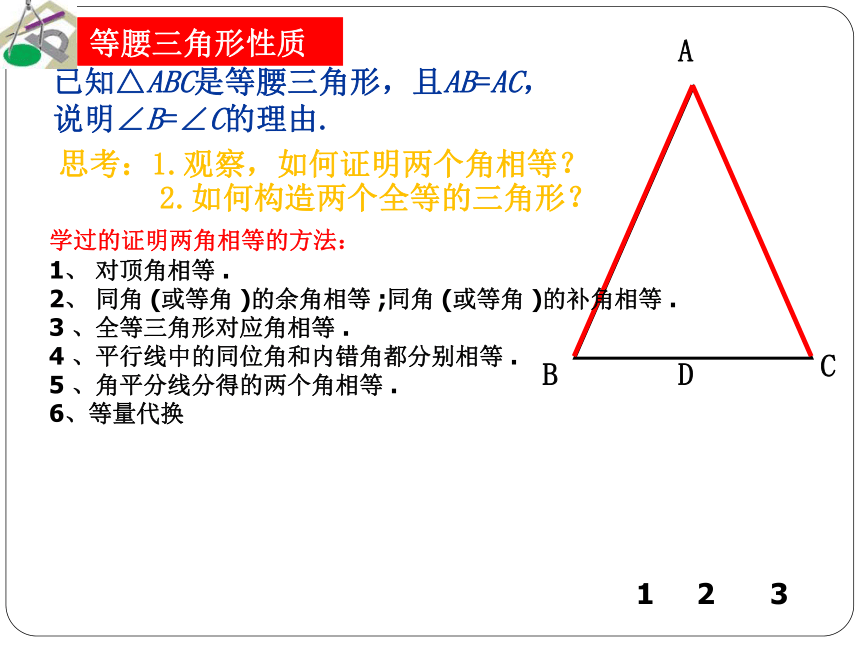
已知△ABC是等腰三角形,且AB=AC,
说明∠B=∠C的理由.D等腰三角形性质思考:1.观察,如何证明两个角相等?2.如何构造两个全等的三角形? 132学过的证明两角相等的方法:
1、 对顶角相等 . 2、 同角 (或等角 )的余角相等 ;同角 (或等角 )的补角相等 . 3 、全等三角形对应角相等 . 4 、平行线中的同位角和内错角都分别相等 . 5 、角平分线分得的两个角相等 .
6、等量代换
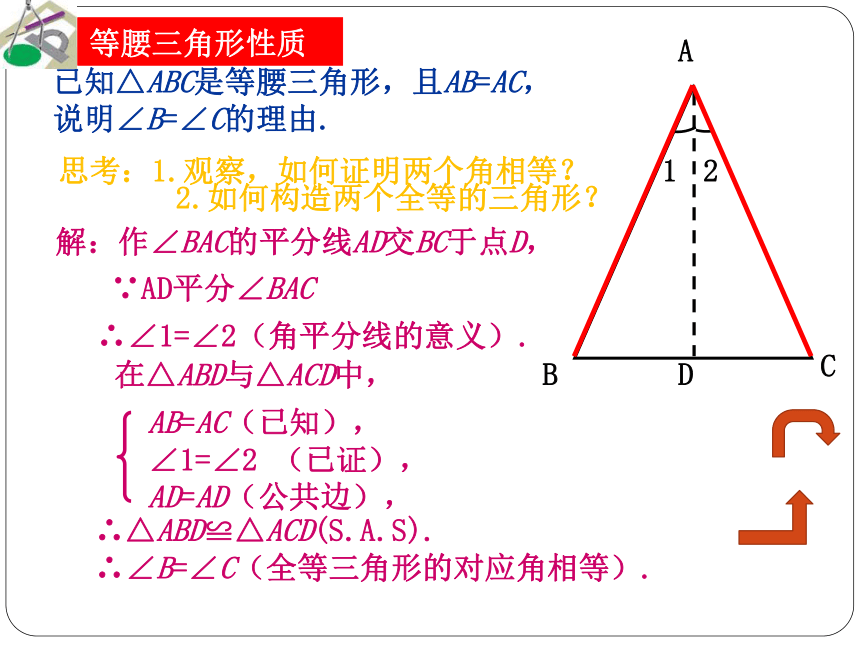
已知△ABC是等腰三角形,且AB=AC,
说明∠B=∠C的理由.解:作∠BAC的平分线AD交BC于点D, ∴∠1=∠2(角平分线的意义).在△ABD与△ACD中,AB=AC(已知),
∠1=∠2 (已证),
AD=AD(公共边), ∴△ABD≌△ACD(S.A.S).
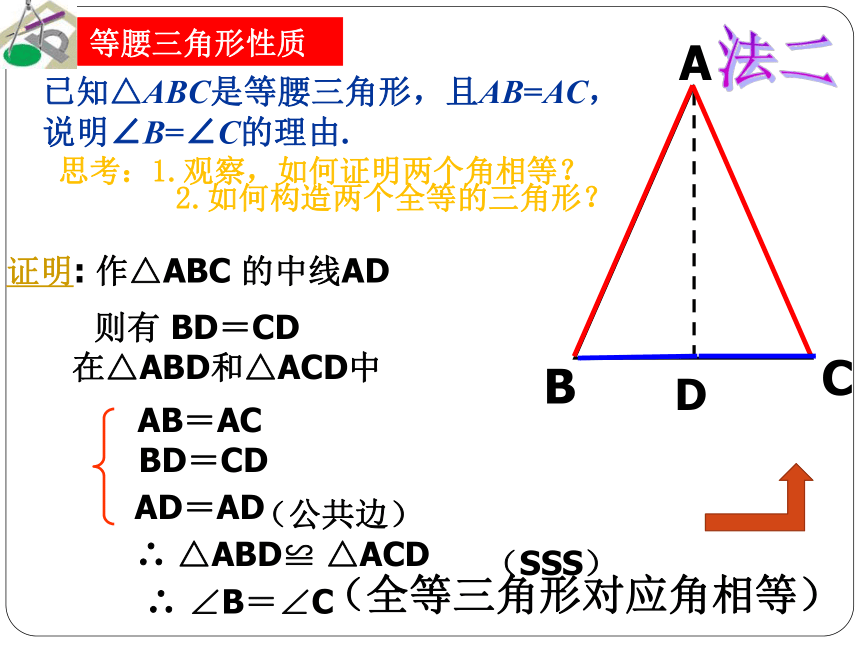
∴∠B=∠C(全等三角形的对应角相等).D12∵AD平分∠BAC思考:1.观察,如何证明两个角相等?2.如何构造两个全等的三角形? 等腰三角形性质则有 BD=CDD在△ABD和△ACD中证明: 作△ABC 的中线ADAB=AC BD=CDAD=AD (公共边) ∴ △ABD≌ △ACD (SSS) ∴ ∠B=∠C (全等三角形对应角相等) 法二已知△ABC是等腰三角形,且AB=AC,
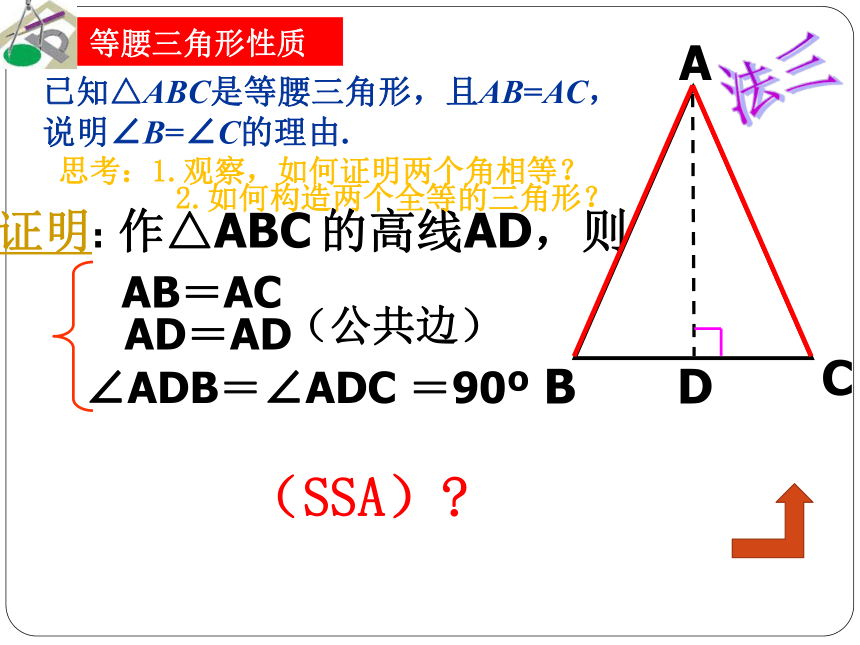
说明∠B=∠C的理由.等腰三角形性质思考:1.观察,如何证明两个角相等?2.如何构造两个全等的三角形? D证明: 作△ABC 的高线AD,则AB=AC AD=AD (公共边) (SSA)? 等腰三角形性质∠ADB=∠ADC =90o已知△ABC是等腰三角形,且AB=AC,
说明∠B=∠C的理由.思考:1.观察,如何证明两个角相等?2.如何构造两个全等的三角形? 法三则有 ∠ADB=∠ADC =90oD在Rt△ABD和Rt△ACD中证明: 作△ABC 的高线ADAB=AC AD=AD (公共边) ∴ Rt△ABD≌Rt△ACD (HL) ∴ ∠B=∠C (全等三角形对应角相等) 等腰三角形性质法三等腰三角形性质1:ACB等腰三角形的两个底角相等
(简称“等边对等角”)符号语言:在△ABC中,
∵ AB = AC (已知)
∴ ∠B = ∠C(等边对等角)前提!等腰三角形性质“等边对等角”常用来证明两角相等、求等腰三角形各角的度数.练一练:
判断正误(口答)
如图,在△ABC中,
∵ AC=BC,
∴ ∠ADC=∠BEC.
已知△ABC是等腰三角形,且AB=AC,
说明∠B=∠C的理由.解:作∠BAC的平分线AD交BC于点D, ∴∠1=∠2(角平分线的意义).在△ABD与△ACD中,AB=AC(已知),
∠1=∠2 (已证),
AD=AD(公共边), ∴△ABD≌△ACD(S.A.S).
∴∠B=∠C(全等三角形的对应角相等).D12∵AD平分∠BAC思考:1.观察,如何证明两个角相等?2.如何构造两个全等的三角形? 等腰三角形性质思考2:结合性质1的操作和推理,从边角关系着眼,还可以得到哪些等量关系?ADCB12结合性质1的操作和推理,从边角关系着眼,
还可以得到哪些等量关系?等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“等腰三角形的三线合一”). 在等腰三角形中,知“一线”得“另两线”.等腰三角形性质2:思考:在运用“等腰三角形的三线合一”时,必须具备几个前提条件?(1)BD=CD,
(2)∠ADB=∠ADC=90°
(3)∠BAD=∠CAD,AD为底边上的中线。AD为底边上的高AD为顶角的平分线 等腰三角形性质 ∵AB=AC,∠1=∠2
∴________________AD⊥BC或BD=CD∵AB=AC,AD⊥BC
∴________________∠1=∠2 或BD=CD∵AB=AC,BD=CD
“等腰三角形的三线合一” 性质几何语言:性质2:(1)(2)(3)等腰三角形性质∴∠1=∠2 或 AD⊥BC等腰三角形性质3:等腰三角形是轴对称图形,
它的对称轴 是 ;顶角平分线所在的直线 底边中线所在的直线,
底边上的高所在的直线.等腰三角形性质在实验操作和论证,我们发现顶角平分线把等腰三角形分成了两个全等的三角形,这说明等腰三角形是一个怎样的图形呢?ABD 注意:今后研究图形的性质时,常从以下几个方面着手:1、边2、角3、特殊线段4、对称性如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断:
①工人师傅在测量了∠B为37°以后,并没有测量∠C ,就说∠C 的度数也是37°.
②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的.请同学们想想:工人师傅的说法对吗?考 考 你理由依据是什么?例1、已知在△ABC中,AB=AC,∠B=70o,
求∠C和∠A的度数。
解:∵AB=AC(已知),
∴∠C=∠B(等边对等角).
∵∠B=70o(已知),
∴∠C=70o(等量代换).
∴∠A=180o-∠B-∠C
=180o-70o-70o=40o (三角形内角和180o)变式一:等腰三角形一个角是70o,求另两角。 变式二:等腰三角形一个角是100o,求另两角。 。 在等腰三角形中,若知一个内角,即可求出另两个内角这类问题需要分类讨论. 等腰三角形的底角可以是直角或钝角吗?为什么?例2、已知:∠BAC=110 o, AB=AC, AD 是BC上的中线.
(1)求∠1、∠2的度数,
(2) AD ? BC 吗?为什么?
解:∵AB=AC, 且AD 是BC上的中线∴∠1=∠2= ∠BAC
(等腰三角形的三线合一)又∵ ∠BAC=110 o∴∠1=∠2= × 110 o=55o (等量代换)ABDC12?(1)(已知)(2)∵AB=AC 且 AD 是BC上的中线(已知)∴ AD ? BC (等腰三角形的三线合一)变式、已知:∠BAC=110 o, AB=AC, AD 是BC上的中线.
(1)求∠1、∠2的度数,
(2) AD ? BC 吗?为什么?
ABDC12AD 是顶角平分线
1. “等边对等角”(等腰三角形的两个底角相等 ).
2. “等腰三角形的三线合一” (等腰三角形的顶角平分线、
底边上的中线、
底边上的高相互重合).
3.等腰三角形是轴对称图形(它的对称轴是:
顶角的平分线所在的直线,
底边中线所在的直线,
底边上的高所在的直线.
课 堂 小 结等腰三角形的性质
(1条)1.判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合.( )
(2)有一个角是60°的等腰三角形,其它两内角也为60°( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××考考你2.等腰三角形的一个外角为140°,那么底角等于( )
A、40° B、100° C、70° D、40°或70
3.已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是( )
A. 8 B. 7 C. 4 D. 3.DB4.如图,已知AB=AC,AD=AE,说明DE∥BC的理由. 解:∵AB=AC(已知)
∴∠B=∠C( )
又∵∠A+∠B+∠C=180°( )
∴∠A+2∠B=180°,即∠B=90°- ______
∵AD=AE(已知)
∴∠____=∠____( )
又∵∠A+∠____+∠____=180°( )
∴∠A+2∠ADE=180°,即∠ADE=90°- ______
∴∠B=∠ADE( )
∴________( ) 等边对等角三角形内角和180°ADEAED等边对等角ADEAED三角形内角和180°等量代换DE∥BC同位角相等,两直线平行考古学家在古共工国墓中发现了大量玉器其中有一种刻叶脉纹的玉三角形饰,呈等腰三角形.现在有一同样刻叶脉纹的玉石残片,如果确定也是等腰三角形,你能用它仅有的底边和一个底角画出它原来的等腰三角形形状吗?学以致用 如何还原残缺的玉器?你能用它仅有的底边AB和一个底角∠B画出它原来的等腰三角形形状吗?ABCABC学以致用
3.结合实验操作,说说等腰三角形底角相等的理由. 操作与思考 操作探究4.思考1:你能用逻辑推理的方法,说明等腰三角形的两个底角相等吗?
已知△ABC是等腰三角形,且AB=AC,
说明∠B=∠C的理由.D等腰三角形性质思考:1.观察,如何证明两个角相等?2.如何构造两个全等的三角形? 132学过的证明两角相等的方法:
1、 对顶角相等 . 2、 同角 (或等角 )的余角相等 ;同角 (或等角 )的补角相等 . 3 、全等三角形对应角相等 . 4 、平行线中的同位角和内错角都分别相等 . 5 、角平分线分得的两个角相等 .
6、等量代换
已知△ABC是等腰三角形,且AB=AC,
说明∠B=∠C的理由.解:作∠BAC的平分线AD交BC于点D, ∴∠1=∠2(角平分线的意义).在△ABD与△ACD中,AB=AC(已知),
∠1=∠2 (已证),
AD=AD(公共边), ∴△ABD≌△ACD(S.A.S).
∴∠B=∠C(全等三角形的对应角相等).D12∵AD平分∠BAC思考:1.观察,如何证明两个角相等?2.如何构造两个全等的三角形? 等腰三角形性质则有 BD=CDD在△ABD和△ACD中证明: 作△ABC 的中线ADAB=AC BD=CDAD=AD (公共边) ∴ △ABD≌ △ACD (SSS) ∴ ∠B=∠C (全等三角形对应角相等) 法二已知△ABC是等腰三角形,且AB=AC,
说明∠B=∠C的理由.等腰三角形性质思考:1.观察,如何证明两个角相等?2.如何构造两个全等的三角形? D证明: 作△ABC 的高线AD,则AB=AC AD=AD (公共边) (SSA)? 等腰三角形性质∠ADB=∠ADC =90o已知△ABC是等腰三角形,且AB=AC,
说明∠B=∠C的理由.思考:1.观察,如何证明两个角相等?2.如何构造两个全等的三角形? 法三则有 ∠ADB=∠ADC =90oD在Rt△ABD和Rt△ACD中证明: 作△ABC 的高线ADAB=AC AD=AD (公共边) ∴ Rt△ABD≌Rt△ACD (HL) ∴ ∠B=∠C (全等三角形对应角相等) 等腰三角形性质法三等腰三角形性质1:ACB等腰三角形的两个底角相等
(简称“等边对等角”)符号语言:在△ABC中,
∵ AB = AC (已知)
∴ ∠B = ∠C(等边对等角)前提!等腰三角形性质“等边对等角”常用来证明两角相等、求等腰三角形各角的度数.练一练:
判断正误(口答)
如图,在△ABC中,
∵ AC=BC,
∴ ∠ADC=∠BEC.
已知△ABC是等腰三角形,且AB=AC,
说明∠B=∠C的理由.解:作∠BAC的平分线AD交BC于点D, ∴∠1=∠2(角平分线的意义).在△ABD与△ACD中,AB=AC(已知),
∠1=∠2 (已证),
AD=AD(公共边), ∴△ABD≌△ACD(S.A.S).
∴∠B=∠C(全等三角形的对应角相等).D12∵AD平分∠BAC思考:1.观察,如何证明两个角相等?2.如何构造两个全等的三角形? 等腰三角形性质思考2:结合性质1的操作和推理,从边角关系着眼,还可以得到哪些等量关系?ADCB12结合性质1的操作和推理,从边角关系着眼,
还可以得到哪些等量关系?等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称为“等腰三角形的三线合一”). 在等腰三角形中,知“一线”得“另两线”.等腰三角形性质2:思考:在运用“等腰三角形的三线合一”时,必须具备几个前提条件?(1)BD=CD,
(2)∠ADB=∠ADC=90°
(3)∠BAD=∠CAD,AD为底边上的中线。AD为底边上的高AD为顶角的平分线 等腰三角形性质 ∵AB=AC,∠1=∠2
∴________________AD⊥BC或BD=CD∵AB=AC,AD⊥BC
∴________________∠1=∠2 或BD=CD∵AB=AC,BD=CD
“等腰三角形的三线合一” 性质几何语言:性质2:(1)(2)(3)等腰三角形性质∴∠1=∠2 或 AD⊥BC等腰三角形性质3:等腰三角形是轴对称图形,
它的对称轴 是 ;顶角平分线所在的直线 底边中线所在的直线,
底边上的高所在的直线.等腰三角形性质在实验操作和论证,我们发现顶角平分线把等腰三角形分成了两个全等的三角形,这说明等腰三角形是一个怎样的图形呢?ABD 注意:今后研究图形的性质时,常从以下几个方面着手:1、边2、角3、特殊线段4、对称性如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断:
①工人师傅在测量了∠B为37°以后,并没有测量∠C ,就说∠C 的度数也是37°.
②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的.请同学们想想:工人师傅的说法对吗?考 考 你理由依据是什么?例1、已知在△ABC中,AB=AC,∠B=70o,
求∠C和∠A的度数。
解:∵AB=AC(已知),
∴∠C=∠B(等边对等角).
∵∠B=70o(已知),
∴∠C=70o(等量代换).
∴∠A=180o-∠B-∠C
=180o-70o-70o=40o (三角形内角和180o)变式一:等腰三角形一个角是70o,求另两角。 变式二:等腰三角形一个角是100o,求另两角。 。 在等腰三角形中,若知一个内角,即可求出另两个内角这类问题需要分类讨论. 等腰三角形的底角可以是直角或钝角吗?为什么?例2、已知:∠BAC=110 o, AB=AC, AD 是BC上的中线.
(1)求∠1、∠2的度数,
(2) AD ? BC 吗?为什么?
解:∵AB=AC, 且AD 是BC上的中线∴∠1=∠2= ∠BAC
(等腰三角形的三线合一)又∵ ∠BAC=110 o∴∠1=∠2= × 110 o=55o (等量代换)ABDC12?(1)(已知)(2)∵AB=AC 且 AD 是BC上的中线(已知)∴ AD ? BC (等腰三角形的三线合一)变式、已知:∠BAC=110 o, AB=AC, AD 是BC上的中线.
(1)求∠1、∠2的度数,
(2) AD ? BC 吗?为什么?
ABDC12AD 是顶角平分线
1. “等边对等角”(等腰三角形的两个底角相等 ).
2. “等腰三角形的三线合一” (等腰三角形的顶角平分线、
底边上的中线、
底边上的高相互重合).
3.等腰三角形是轴对称图形(它的对称轴是:
顶角的平分线所在的直线,
底边中线所在的直线,
底边上的高所在的直线.
课 堂 小 结等腰三角形的性质
(1条)1.判断下列语句是否正确。(1)等腰三角形的角平分线、中线和高互相重合.( )
(2)有一个角是60°的等腰三角形,其它两内角也为60°( )
(3)等腰三角形的底角都是锐角. ( )
(4)钝角三角形不可能是等腰三角形 . ( )××考考你2.等腰三角形的一个外角为140°,那么底角等于( )
A、40° B、100° C、70° D、40°或70
3.已知等腰三角形的两条边长分别是7和3,则下列四个数中,第三条边的长是( )
A. 8 B. 7 C. 4 D. 3.DB4.如图,已知AB=AC,AD=AE,说明DE∥BC的理由. 解:∵AB=AC(已知)
∴∠B=∠C( )
又∵∠A+∠B+∠C=180°( )
∴∠A+2∠B=180°,即∠B=90°- ______
∵AD=AE(已知)
∴∠____=∠____( )
又∵∠A+∠____+∠____=180°( )
∴∠A+2∠ADE=180°,即∠ADE=90°- ______
∴∠B=∠ADE( )
∴________( ) 等边对等角三角形内角和180°ADEAED等边对等角ADEAED三角形内角和180°等量代换DE∥BC同位角相等,两直线平行考古学家在古共工国墓中发现了大量玉器其中有一种刻叶脉纹的玉三角形饰,呈等腰三角形.现在有一同样刻叶脉纹的玉石残片,如果确定也是等腰三角形,你能用它仅有的底边和一个底角画出它原来的等腰三角形形状吗?学以致用 如何还原残缺的玉器?你能用它仅有的底边AB和一个底角∠B画出它原来的等腰三角形形状吗?ABCABC学以致用
