14.5 等腰三角形的性质 课件(26张PPT)
文档属性
| 名称 | 14.5 等腰三角形的性质 课件(26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览






文档简介
课件26张PPT。14.5等腰三角形的性质一、引入等腰三角形ABC有两条边相等的三角形,
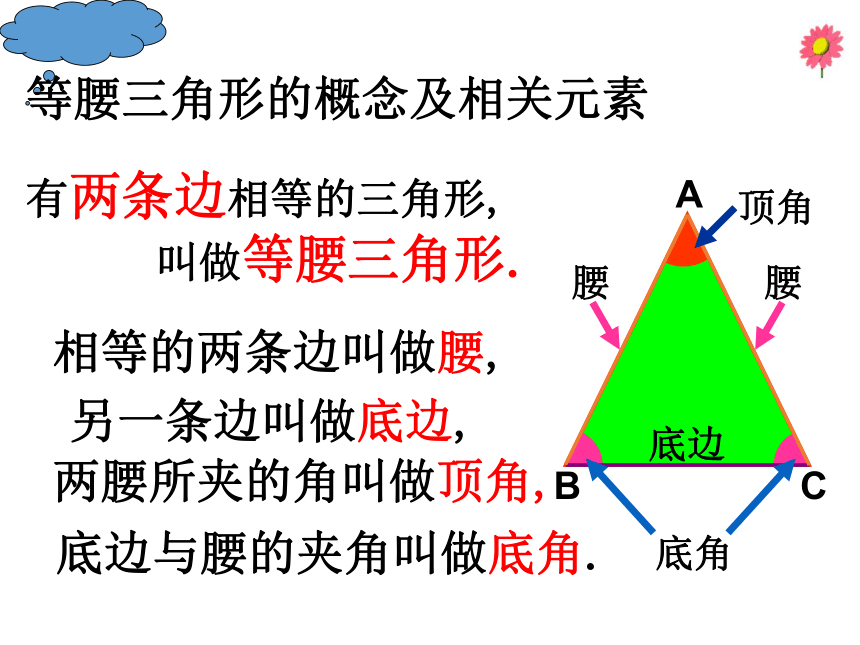
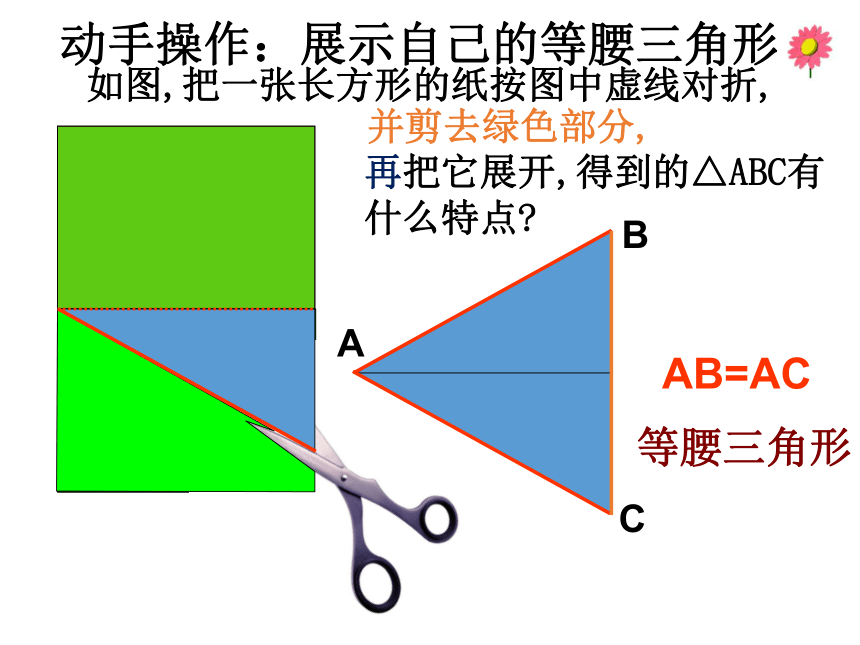
叫做等腰三角形.相等的两条边叫做腰,另一条边叫做底边,底边与腰的夹角叫做底角.两腰所夹的角叫做顶角,腰腰底边顶角底角等腰三角形的概念及相关元素如图,把一张长方形的纸按图中虚线对折, 并剪去绿色部分, 再把它展开,得到的△ABC有什么特点?ABCAB=AC等腰三角形动手操作:展示自己的等腰三角形 (2)等腰三角形的角; (1)等腰三角形的边;
猜测等腰三角形的特点。 (3)等腰三角形的对称性;问题1:思考:如何几何论证说理等腰三角形的两个底角相等呢?想一想:如何证明两个角相等? 如何构造两个全等的三角形?方法2:作底边上的中线方法1:作顶角的平分线方法3:作底边的高已知: 如图,在△ABC中,AB=AC.
说明: ∠B= ∠C.D解: 作顶角的平分线AD,则∠1=∠2AB=AC ( 已知 )∠1=∠2 ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).作顶角的平分线在△BAD和△CAD中12性质1:
等腰三角形的两个底角相等
(简称为“等边对等角”)
符号表达式:
在△ABC中
∵ AB=AC(已知)
∴ ∠C=∠B(等边对等角)填空:
在△ABC中,
∵AB=CB (已知)
∴∠_____=∠_____
CA(__________)
等边对等角在说理过程中,除了可以得到两底角相等,还可以得到其他结论吗?问题2:观察:在△ABC中,AB=AC,∠1=∠2.
(1)猜测线段BD、CD的数量关系,
(2)线段AD、BC的位置关系. 1 2 已知: 如图,在△ABC中,AB=AC.
说明: ∠B= ∠C.D解: 作顶角的平分线AD,则∠1=∠2AB=AC ( 已知 )∠1=∠2 ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).作顶角的平分线在△BAD和△CAD中12341 2 线段AD既是顶角∠BAC的______线,
又是底边BC边上的____线,
还是底边BC边上的____.角平分中高性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
(简称为“等腰三角形的三线合一”)
唯一性在△ABC中
∵ AB=AC,∠1=∠2(已知)
∴ BD=CD,AD⊥BC(等腰三角形的三线合一)
在△ABC中
∵ AB=AC,BD=CD(已知)
∴AD⊥BC,∠1=∠2(等腰三角形的三线合一)
在△ABC中
∵ AB=AC,AD⊥BC(已知)
∴ BD=CD,∠1=∠2(等腰三角形的三线合一)
1 2 1. 根据等腰三角形性质2填空,
在△ABC中, AB=AC, ∵AD⊥BC,
∴∠_____ = ∠_____,____= ____. (2) ∵AD是中线,∴____⊥____ ,
∠_____ =∠_____.(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCD小试牛刀性质3:等腰三角形是轴对称图形,它的对称轴是顶角平分线所在的直线.等腰三角形的对称轴是( )
(A)顶角的平分线
(B)底边上的高
(C)底边上的中线
(D)底边上的高所在直线 D性质应用例题1:已知在△ABC中,AB=AC.
∠B=70°,求∠C和∠A的度数。∠C=70° ∠A= 40°性质应用例题1:已知在△ABC中,AB=AC.∠B=70°,求∠C和∠A的度数。变式1:若∠A=70°,
求 ∠C和∠B的度数呢?变式2:若等腰三角形的一个角是50° ,则另外两个角为( )。∠C=55° ∠B= 55°65°, 65°或 80° ,50° ,例题2:如图,△ABC中,AB=AC.
∠BAC= 110°,AD是△ABC的中线。
(1)求∠1、 ∠2的度数.
(2) AD⊥BC吗?为什么?
55° 垂直若AD是△ABC的角平分线呢?性质应用 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。ABCD拓展与提高课堂小结
叫做等腰三角形.相等的两条边叫做腰,另一条边叫做底边,底边与腰的夹角叫做底角.两腰所夹的角叫做顶角,腰腰底边顶角底角等腰三角形的概念及相关元素如图,把一张长方形的纸按图中虚线对折, 并剪去绿色部分, 再把它展开,得到的△ABC有什么特点?ABCAB=AC等腰三角形动手操作:展示自己的等腰三角形 (2)等腰三角形的角; (1)等腰三角形的边;
猜测等腰三角形的特点。 (3)等腰三角形的对称性;问题1:思考:如何几何论证说理等腰三角形的两个底角相等呢?想一想:如何证明两个角相等? 如何构造两个全等的三角形?方法2:作底边上的中线方法1:作顶角的平分线方法3:作底边的高已知: 如图,在△ABC中,AB=AC.
说明: ∠B= ∠C.D解: 作顶角的平分线AD,则∠1=∠2AB=AC ( 已知 )∠1=∠2 ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).作顶角的平分线在△BAD和△CAD中12性质1:
等腰三角形的两个底角相等
(简称为“等边对等角”)
符号表达式:
在△ABC中
∵ AB=AC(已知)
∴ ∠C=∠B(等边对等角)填空:
在△ABC中,
∵AB=CB (已知)
∴∠_____=∠_____
CA(__________)
等边对等角在说理过程中,除了可以得到两底角相等,还可以得到其他结论吗?问题2:观察:在△ABC中,AB=AC,∠1=∠2.
(1)猜测线段BD、CD的数量关系,
(2)线段AD、BC的位置关系. 1 2 已知: 如图,在△ABC中,AB=AC.
说明: ∠B= ∠C.D解: 作顶角的平分线AD,则∠1=∠2AB=AC ( 已知 )∠1=∠2 ( 已作 )AD=AD (公共边) ∴ △BAD ≌ △CAD (SAS).∴ ∠ B= ∠C (全等三角形的对应角相等).作顶角的平分线在△BAD和△CAD中12341 2 线段AD既是顶角∠BAC的______线,
又是底边BC边上的____线,
还是底边BC边上的____.角平分中高性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
(简称为“等腰三角形的三线合一”)
唯一性在△ABC中
∵ AB=AC,∠1=∠2(已知)
∴ BD=CD,AD⊥BC(等腰三角形的三线合一)
在△ABC中
∵ AB=AC,BD=CD(已知)
∴AD⊥BC,∠1=∠2(等腰三角形的三线合一)
在△ABC中
∵ AB=AC,AD⊥BC(已知)
∴ BD=CD,∠1=∠2(等腰三角形的三线合一)
1 2 1. 根据等腰三角形性质2填空,
在△ABC中, AB=AC, ∵AD⊥BC,
∴∠_____ = ∠_____,____= ____. (2) ∵AD是中线,∴____⊥____ ,
∠_____ =∠_____.(3) ∵AD是角平分线,∴____ ⊥____ ,_____ =_____.BADCADCADBDCDADBCBDBADBCADCD小试牛刀性质3:等腰三角形是轴对称图形,它的对称轴是顶角平分线所在的直线.等腰三角形的对称轴是( )
(A)顶角的平分线
(B)底边上的高
(C)底边上的中线
(D)底边上的高所在直线 D性质应用例题1:已知在△ABC中,AB=AC.
∠B=70°,求∠C和∠A的度数。∠C=70° ∠A= 40°性质应用例题1:已知在△ABC中,AB=AC.∠B=70°,求∠C和∠A的度数。变式1:若∠A=70°,
求 ∠C和∠B的度数呢?变式2:若等腰三角形的一个角是50° ,则另外两个角为( )。∠C=55° ∠B= 55°65°, 65°或 80° ,50° ,例题2:如图,△ABC中,AB=AC.
∠BAC= 110°,AD是△ABC的中线。
(1)求∠1、 ∠2的度数.
(2) AD⊥BC吗?为什么?
55° 垂直若AD是△ABC的角平分线呢?性质应用 如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。ABCD拓展与提高课堂小结
