14.5 等腰三角形的性质(1) 课件(19张PPT)
文档属性
| 名称 | 14.5 等腰三角形的性质(1) 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 495.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 17:35:56 | ||
图片预览



文档简介
课件19张PPT。14.5 等腰三角形的性质(1)等腰三角形的定义是什么?
有两条边相等的三角形是等腰三角形.
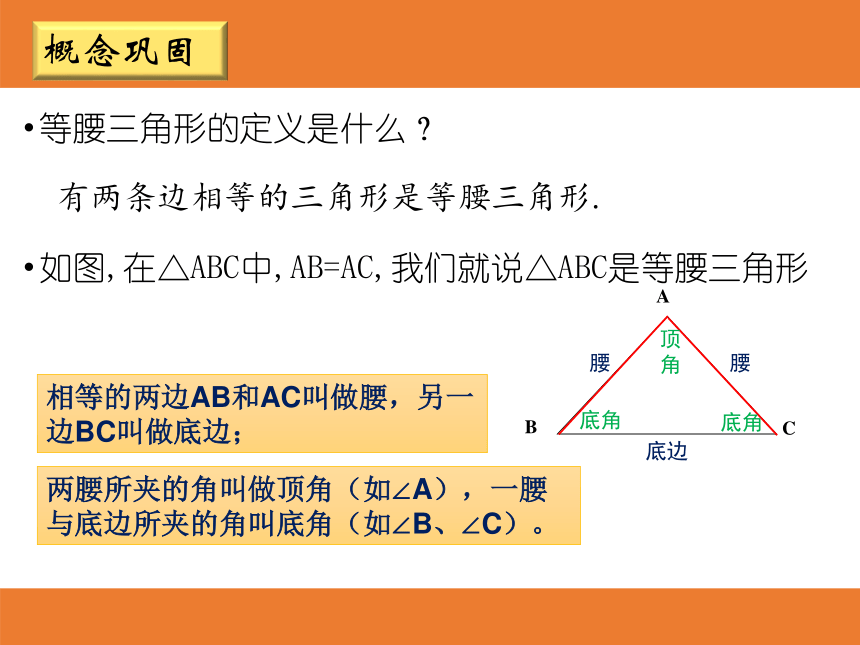
如图,在△ABC中,AB=AC,我们就说△ABC是等腰三角形
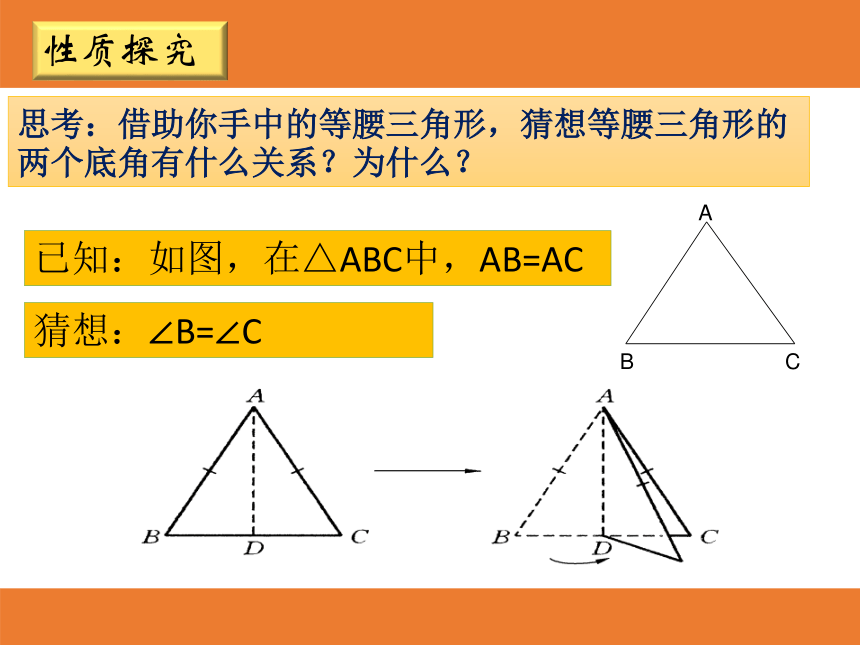
相等的两边AB和AC叫做腰,另一边BC叫做底边;腰腰底边顶角底角底角两腰所夹的角叫做顶角(如∠A),一腰与底边所夹的角叫底角(如∠B、∠C)。概念巩固思考:借助你手中的等腰三角形,猜想等腰三角形的两个底角有什么关系?为什么?已知:如图,在△ABC中,AB=AC猜想:∠B=∠C性质探究思考:如何将刚才的操作加以说理,得到∠B=∠C ?找到等腰三角形ABC顶角∠A的平分线AD,
将△ABD沿AD所在的直线AD翻折后,射线 与射线 叠合.
由于AB=AC,因此线段 与线段 重合.
又因为点D与点D重合,所以线段 与线段 也重合.
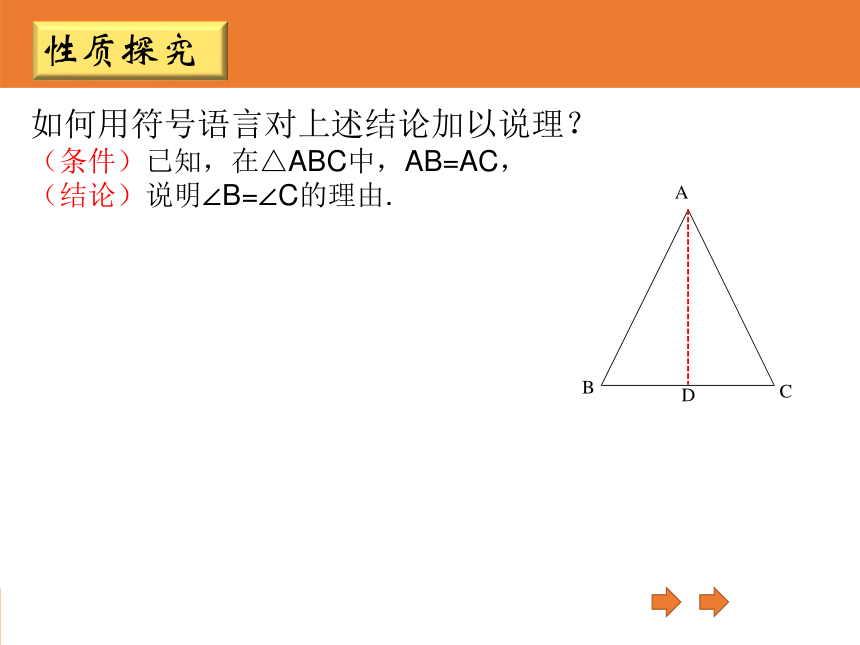
因此∠B=∠C.叠合法ABACABACBDCD性质探究通过叠合我们还发现等腰三角形是轴对称图形.D如何用符号语言对上述结论加以说理?
(条件)已知,在△ABC中,AB=AC,
(结论)说明∠B=∠C的理由.性质探究解:过点A作∠BAC的平分线AD,交BC于点D
∵AD平分∠BAC
∴∠BAD=∠CAD(角平分线的意义).
在△ABD与△ACD中,
AB=AC(已知)
∠BAD=∠CAD(已求)
AD=AD(公共边)
∴△ABD≌△ACD(S.A.S).
∴∠B=∠C(全等三角形的对应角相等)
D如何用符号语言对上述结论加以说理?
(条件)已知,在△ABC中,AB=AC,
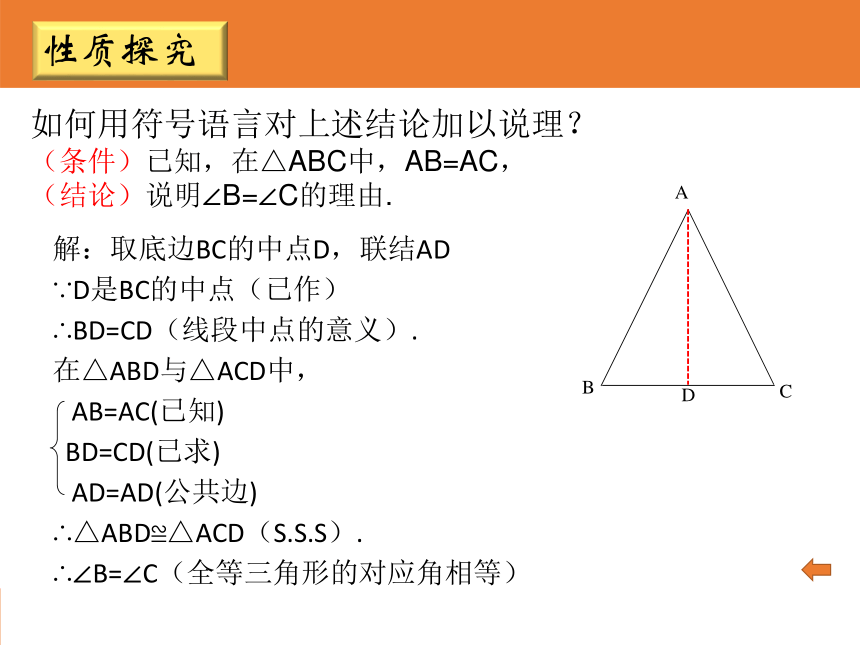
(结论)说明∠B=∠C的理由.性质探究解:取底边BC的中点D,联结AD
∵D是BC的中点(已作)
∴BD=CD(线段中点的意义).
在△ABD与△ACD中,
AB=AC(已知)
BD=CD(已求)
AD=AD(公共边)
∴△ABD≌△ACD(S.S.S).
∴∠B=∠C(全等三角形的对应角相等)
D如何用符号语言对上述结论加以说理?
(条件)已知,在△ABC中,AB=AC,
(结论)说明∠B=∠C的理由.性质探究等腰三角形的性质一:等腰三角形的两个底角相等。
(简称“等边对等角” )符号语言:在△ABC中,
∵ AB=AC(已知)
∴∠B=∠C__________思考:该结论如何用符号语言表述?(等边对等角)
性质探究例题 如图,已知AB=AC,∠B=70°,求∠C的度数;
解:在△ABC中,
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=70°(已知)
∴ ∠C=70°(等量代换)ABC性质应用思考1:通过全等,你还能得到哪些等量关系?D∵△ABD≌△ACD(已求).
∴BD=CD(全等三角形的对应边相等)
∴∠ADB=∠ADC(全等三角形的对应角相等)
又∵∠ADB+∠ADC=180°(邻补角的意义)
∴2∠ADB=2∠ADC=180°(等量代换)
∴∠ADB=∠ADC=90°(等式性质)性质探究解:过点A作∠BAC的平分线AD,交BC于点D
……
∴△ABD≌△ACD(SAS)D∵△ABD≌△ACD(已求).
∴BD=CD(全等三角形的对应边相等)
∴∠ADB=∠ADC(全等三角形的对应角相等)
又∵∠ADB+∠ADC=180°(邻补角的意义)
∴2∠ADB=2∠ADC=180°(等量代换)
∴∠ADB=∠ADC=90°(等式性质)思考2:通过这些结论你发现了什么?等腰三角形ABC的顶角∠A的平分线AD同时也是底边上的中线、底边上的高.性质探究等腰三角形的性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
D思考并讨论:上述性质可以如何分解?如何用符号语言来表达?性质探究在△ABC中,
∵AB=AC, ∠BAD=∠CAD (已知)
∴________________
________________BD=CD符号语言1等腰三角形的三线合一 D等腰三角形的性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
(等腰三角形的顶角平分线是底边上的中线)AD⊥BC(等腰三角形的顶角平分线是底边上的高)在△ABC中,
∵AB=AC, BD=CD (已知)
∴________________
________________∠BAD=∠CAD符号语言2等腰三角形的三线合一 D等腰三角形的性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
(等腰三角形的底边上的中线是顶角平分线)AD⊥BC(等腰三角形底边上的中线是底边上的高)在△ABC中,
∵AB=AC, AD⊥BC(已知)
∴_________
_________符号语言3等腰三角形的三线合一 D等腰三角形的性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
(等腰三角形底边上的高是顶角平分线)∠BAD=∠CAD (等腰三角形底边上的高是底边上的中线)BD=CD 如图,在△ABC中,AB=AC. 若BD是∠ABC的平分线,那么BD一定是AC边上的中线或者高吗?D等腰三角形的性质一:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
性质辨析本课小结等腰三角形与不等边三角形相比有何特殊之处?等腰三角形的性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
等腰三角形的性质一:等腰三角形的两个底角相等。 (简称“等边对等角” )等腰三角形是轴对称图形神秘符号在古代埃及和巴比伦,一些测量工具和基本的几何图形,往往成了神圣的符号而被人们用作护身符.
下图是埃及古墓中出土的形如测量工具的护身符,也是一个测水准的工具.
古代的水准仪由一个等腰三角形及悬挂在顶点处的铅垂线组成,如右图所示。测量时,调整底边的位置,如果铅垂线经过底边中点,就表明底边垂直于铅垂线,即底边是水平的。
埃及古墓中出土的水准仪性质应用
有两条边相等的三角形是等腰三角形.
如图,在△ABC中,AB=AC,我们就说△ABC是等腰三角形
相等的两边AB和AC叫做腰,另一边BC叫做底边;腰腰底边顶角底角底角两腰所夹的角叫做顶角(如∠A),一腰与底边所夹的角叫底角(如∠B、∠C)。概念巩固思考:借助你手中的等腰三角形,猜想等腰三角形的两个底角有什么关系?为什么?已知:如图,在△ABC中,AB=AC猜想:∠B=∠C性质探究思考:如何将刚才的操作加以说理,得到∠B=∠C ?找到等腰三角形ABC顶角∠A的平分线AD,
将△ABD沿AD所在的直线AD翻折后,射线 与射线 叠合.
由于AB=AC,因此线段 与线段 重合.
又因为点D与点D重合,所以线段 与线段 也重合.
因此∠B=∠C.叠合法ABACABACBDCD性质探究通过叠合我们还发现等腰三角形是轴对称图形.D如何用符号语言对上述结论加以说理?
(条件)已知,在△ABC中,AB=AC,
(结论)说明∠B=∠C的理由.性质探究解:过点A作∠BAC的平分线AD,交BC于点D
∵AD平分∠BAC
∴∠BAD=∠CAD(角平分线的意义).
在△ABD与△ACD中,
AB=AC(已知)
∠BAD=∠CAD(已求)
AD=AD(公共边)
∴△ABD≌△ACD(S.A.S).
∴∠B=∠C(全等三角形的对应角相等)
D如何用符号语言对上述结论加以说理?
(条件)已知,在△ABC中,AB=AC,
(结论)说明∠B=∠C的理由.性质探究解:取底边BC的中点D,联结AD
∵D是BC的中点(已作)
∴BD=CD(线段中点的意义).
在△ABD与△ACD中,
AB=AC(已知)
BD=CD(已求)
AD=AD(公共边)
∴△ABD≌△ACD(S.S.S).
∴∠B=∠C(全等三角形的对应角相等)
D如何用符号语言对上述结论加以说理?
(条件)已知,在△ABC中,AB=AC,
(结论)说明∠B=∠C的理由.性质探究等腰三角形的性质一:等腰三角形的两个底角相等。
(简称“等边对等角” )符号语言:在△ABC中,
∵ AB=AC(已知)
∴∠B=∠C__________思考:该结论如何用符号语言表述?(等边对等角)
性质探究例题 如图,已知AB=AC,∠B=70°,求∠C的度数;
解:在△ABC中,
∵AB=AC(已知)
∴∠B=∠C(等边对等角)
∵∠B=70°(已知)
∴ ∠C=70°(等量代换)ABC性质应用思考1:通过全等,你还能得到哪些等量关系?D∵△ABD≌△ACD(已求).
∴BD=CD(全等三角形的对应边相等)
∴∠ADB=∠ADC(全等三角形的对应角相等)
又∵∠ADB+∠ADC=180°(邻补角的意义)
∴2∠ADB=2∠ADC=180°(等量代换)
∴∠ADB=∠ADC=90°(等式性质)性质探究解:过点A作∠BAC的平分线AD,交BC于点D
……
∴△ABD≌△ACD(SAS)D∵△ABD≌△ACD(已求).
∴BD=CD(全等三角形的对应边相等)
∴∠ADB=∠ADC(全等三角形的对应角相等)
又∵∠ADB+∠ADC=180°(邻补角的意义)
∴2∠ADB=2∠ADC=180°(等量代换)
∴∠ADB=∠ADC=90°(等式性质)思考2:通过这些结论你发现了什么?等腰三角形ABC的顶角∠A的平分线AD同时也是底边上的中线、底边上的高.性质探究等腰三角形的性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
D思考并讨论:上述性质可以如何分解?如何用符号语言来表达?性质探究在△ABC中,
∵AB=AC, ∠BAD=∠CAD (已知)
∴________________
________________BD=CD符号语言1等腰三角形的三线合一 D等腰三角形的性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
(等腰三角形的顶角平分线是底边上的中线)AD⊥BC(等腰三角形的顶角平分线是底边上的高)在△ABC中,
∵AB=AC, BD=CD (已知)
∴________________
________________∠BAD=∠CAD符号语言2等腰三角形的三线合一 D等腰三角形的性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
(等腰三角形的底边上的中线是顶角平分线)AD⊥BC(等腰三角形底边上的中线是底边上的高)在△ABC中,
∵AB=AC, AD⊥BC(已知)
∴_________
_________符号语言3等腰三角形的三线合一 D等腰三角形的性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
(等腰三角形底边上的高是顶角平分线)∠BAD=∠CAD (等腰三角形底边上的高是底边上的中线)BD=CD 如图,在△ABC中,AB=AC. 若BD是∠ABC的平分线,那么BD一定是AC边上的中线或者高吗?D等腰三角形的性质一:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
性质辨析本课小结等腰三角形与不等边三角形相比有何特殊之处?等腰三角形的性质二:
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“等腰三角形的三线合一”)
等腰三角形的性质一:等腰三角形的两个底角相等。 (简称“等边对等角” )等腰三角形是轴对称图形神秘符号在古代埃及和巴比伦,一些测量工具和基本的几何图形,往往成了神圣的符号而被人们用作护身符.
下图是埃及古墓中出土的形如测量工具的护身符,也是一个测水准的工具.
古代的水准仪由一个等腰三角形及悬挂在顶点处的铅垂线组成,如右图所示。测量时,调整底边的位置,如果铅垂线经过底边中点,就表明底边垂直于铅垂线,即底边是水平的。
埃及古墓中出土的水准仪性质应用
