14.6(1)等腰三角形的判定 课件(17张)
文档属性
| 名称 | 14.6(1)等腰三角形的判定 课件(17张) |

|
|
| 格式 | zip | ||
| 文件大小 | 308.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 17:35:56 | ||
图片预览






文档简介
课件16张PPT。14.6(1)等腰三角形的判定课前回顾课前回顾Part 1Part 1 课前练习A
B
C
D
如图,在△ABC中AB=AD=DC,
∠BAD=26o,
则∠B=__ 度,∠C=___度。思考:在计算过程中,主要运用了什么性质?等边对等角7738.5新课探索新课探索Part 1Part 1 猜想想判定一个三角形是等腰三角形,你有些什么方法?1、根据等腰三角形的定义2、由等腰三角形的性质,猜想:
有两个角相等的三角形是等腰三角形吗?新课探索Part 1Part 2 论证猜想如图,在△ABC中,
∠B=∠C,
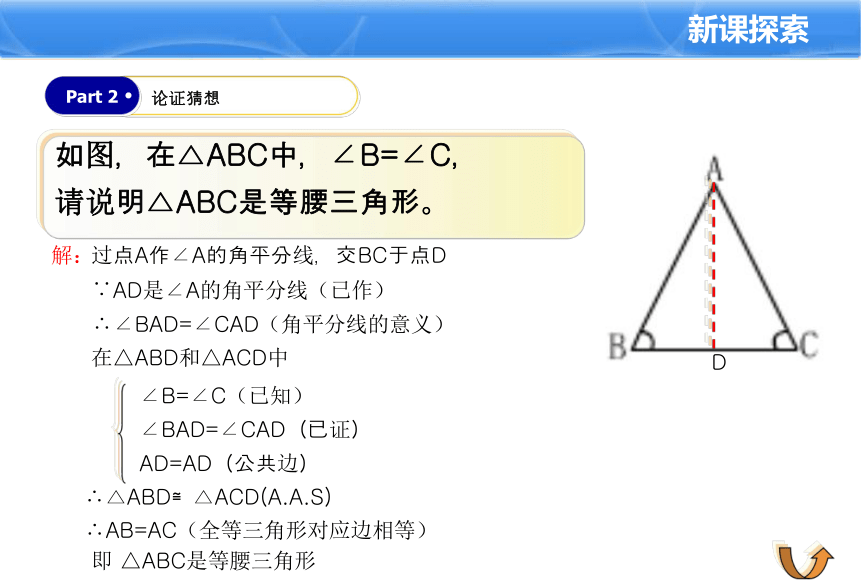
请说明△ABC是等腰三角形。只有这一种方法吗?新课探索Part 1Part 2 论证猜想如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。解:过点A作∠A的角平分线,交BC于点DD∵AD是∠A的角平分线(已作)∴∠BAD=∠CAD(角平分线的意义)在△ABD和△ACD中∠B=∠C(已知)
∠BAD=∠CAD(已证)
AD=AD(公共边)∴△ABD≌△ACD(A.A.S)∴AB=AC(全等三角形对应边相等)即 △ABC是等腰三角形新课探索Part 1Part 2 论证猜想如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。解:过点A作AD⊥BC,垂足为DD∵AD⊥BC(已作)∴∠BDA=90°,∠CDA=90°(垂直的意义)在△ABD和△ACD中∠B=∠C(已知)
∠BDA=∠CDA(已证)
AD=AD(公共边)∴△ABD≌△ACD(A.A.S)∴AB=AC(全等三角形对应边相等)即 △ABC是等腰三角形∴∠BDA=∠CDA(等量代换)新课探索Part 1Part 2 论证猜想如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。解:取BC的中点D,联结ADD∵点D是BD的中点(已作)∴BD=DC(线段中点的意义)思考:还能继续证明下去吗?新课探索Part 1Part 2 论证猜想等腰三角形的判定方法:如果一个三角形有两个角相等,
那么这两个角所对的边也相等,
这个三角形是等腰三角形。
(简称为“等角对等边”)∵∠B=∠C几何语言表达:∴AB=AC(等角对等边)即:△ABC是等腰三角形新课探索回忆旧知:如图,在△ABC中,
已知BD、CE分别是AC、AB上的高,
BD、CE交与点O,且∠DBC=∠ECB,
说明OE=OD的理由。你能不能用一次全等证明来完成说明呢?解:∵∠DBC=∠ECB(已知)∴OB=OC(等角对等边)∵CE⊥AB(已知)∴∠CEB=90°(垂直意义)同理 ∠BDC=90°∴∠CEB=∠BDC(等量代换)在△OEB和△ODC中∠CEB=∠BDC(已证)
∠EOB=∠DOC(对顶角相等)
OB=OC(已证)∴△OEB≌△ODC(A.A.S)∴OE=OD(全等三角形对应边相等)新课探索例题1:如图,在△ABC中,
已知BD、CE分别是AC、AB上的高,
且∠DBC=∠ECB,
说明△ABC是等腰三角形的理由。新课探索例题2:如图,在△ABC中,BD平分∠ABC,
过点D作BC的平行线DE,交AB于E,
试说明DE=BE的理由。Part 1Part 3 课内练习A
解:∵BD平分∠ABC(已知)∴∠ABD=∠DBC(角平分线的意义)∵DE//BC(已知)∴∠DBC=∠EDB(两直线平行,内错角相等)∴∠ABD=∠EDB(等量代换)∴BE=DE(等角对等边)课堂练习变式训练1:如图在△ABC中, DE=BE ,BC//DE,
试说明 BD平分∠ABC的理由。变式训练2:如图在△ABC中, DE=BE ,
BD平分∠ABC ,
试说明DE//BC 的理由。练习册57页第3题 课后作业本课小结这节课你的收获是什么?
B
C
D
如图,在△ABC中AB=AD=DC,
∠BAD=26o,
则∠B=__ 度,∠C=___度。思考:在计算过程中,主要运用了什么性质?等边对等角7738.5新课探索新课探索Part 1Part 1 猜想想判定一个三角形是等腰三角形,你有些什么方法?1、根据等腰三角形的定义2、由等腰三角形的性质,猜想:
有两个角相等的三角形是等腰三角形吗?新课探索Part 1Part 2 论证猜想如图,在△ABC中,
∠B=∠C,
请说明△ABC是等腰三角形。只有这一种方法吗?新课探索Part 1Part 2 论证猜想如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。解:过点A作∠A的角平分线,交BC于点DD∵AD是∠A的角平分线(已作)∴∠BAD=∠CAD(角平分线的意义)在△ABD和△ACD中∠B=∠C(已知)
∠BAD=∠CAD(已证)
AD=AD(公共边)∴△ABD≌△ACD(A.A.S)∴AB=AC(全等三角形对应边相等)即 △ABC是等腰三角形新课探索Part 1Part 2 论证猜想如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。解:过点A作AD⊥BC,垂足为DD∵AD⊥BC(已作)∴∠BDA=90°,∠CDA=90°(垂直的意义)在△ABD和△ACD中∠B=∠C(已知)
∠BDA=∠CDA(已证)
AD=AD(公共边)∴△ABD≌△ACD(A.A.S)∴AB=AC(全等三角形对应边相等)即 △ABC是等腰三角形∴∠BDA=∠CDA(等量代换)新课探索Part 1Part 2 论证猜想如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。解:取BC的中点D,联结ADD∵点D是BD的中点(已作)∴BD=DC(线段中点的意义)思考:还能继续证明下去吗?新课探索Part 1Part 2 论证猜想等腰三角形的判定方法:如果一个三角形有两个角相等,
那么这两个角所对的边也相等,
这个三角形是等腰三角形。
(简称为“等角对等边”)∵∠B=∠C几何语言表达:∴AB=AC(等角对等边)即:△ABC是等腰三角形新课探索回忆旧知:如图,在△ABC中,
已知BD、CE分别是AC、AB上的高,
BD、CE交与点O,且∠DBC=∠ECB,
说明OE=OD的理由。你能不能用一次全等证明来完成说明呢?解:∵∠DBC=∠ECB(已知)∴OB=OC(等角对等边)∵CE⊥AB(已知)∴∠CEB=90°(垂直意义)同理 ∠BDC=90°∴∠CEB=∠BDC(等量代换)在△OEB和△ODC中∠CEB=∠BDC(已证)
∠EOB=∠DOC(对顶角相等)
OB=OC(已证)∴△OEB≌△ODC(A.A.S)∴OE=OD(全等三角形对应边相等)新课探索例题1:如图,在△ABC中,
已知BD、CE分别是AC、AB上的高,
且∠DBC=∠ECB,
说明△ABC是等腰三角形的理由。新课探索例题2:如图,在△ABC中,BD平分∠ABC,
过点D作BC的平行线DE,交AB于E,
试说明DE=BE的理由。Part 1Part 3 课内练习A
解:∵BD平分∠ABC(已知)∴∠ABD=∠DBC(角平分线的意义)∵DE//BC(已知)∴∠DBC=∠EDB(两直线平行,内错角相等)∴∠ABD=∠EDB(等量代换)∴BE=DE(等角对等边)课堂练习变式训练1:如图在△ABC中, DE=BE ,BC//DE,
试说明 BD平分∠ABC的理由。变式训练2:如图在△ABC中, DE=BE ,
BD平分∠ABC ,
试说明DE//BC 的理由。练习册57页第3题 课后作业本课小结这节课你的收获是什么?
