14.6(1)等腰三角形的判定 课件(17张PPT)
文档属性
| 名称 | 14.6(1)等腰三角形的判定 课件(17张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 175.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 17:35:56 | ||
图片预览





文档简介
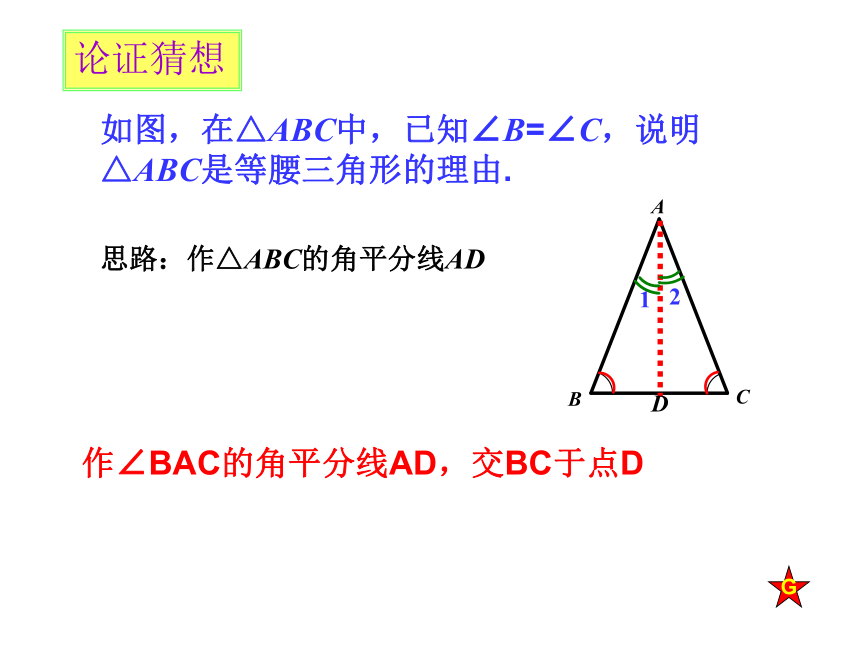
课件17张PPT。折纸实验如图,将一个长方形纸条进行折叠,当叠合部分是一个三角形且折叠后长方形的四个顶点都不在长方形内部时,这个三角形必是一个等腰三角形。14.6等腰三角形的判定(1) 1.什么是等腰三角形?
定义:有两条边相等的三角形叫等腰三角形
2.等腰三角形有哪些性质?
等边对等角
等腰三角形三线合一
复习平行线的性质:两直线平行,内错角相等
平行线的判定:内错角相等,两直线平行
等腰三角形的性质:等边对等角
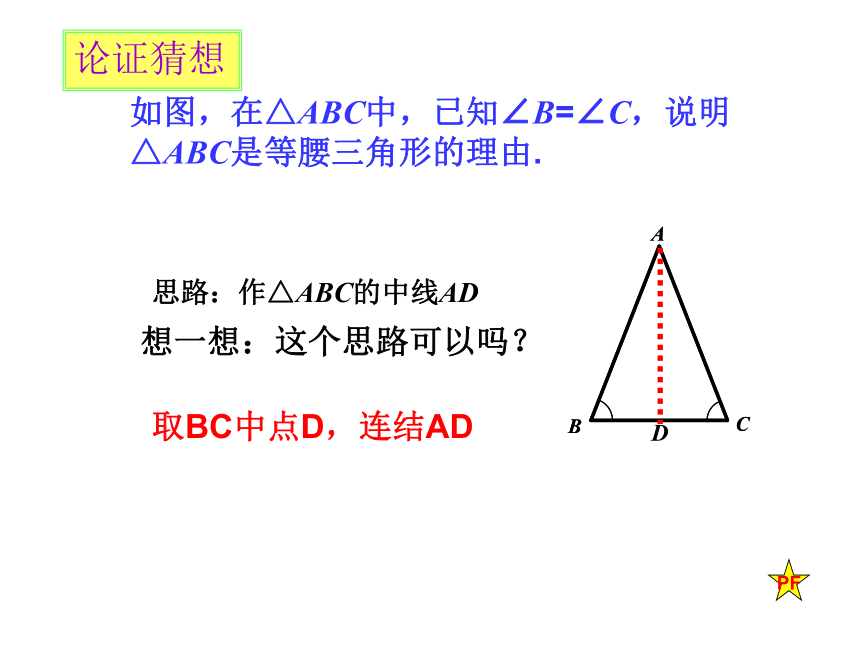
等腰三角形的判定:等角对等边猜一猜论证猜想如图,在△ABC中,已知∠B=∠C,说明△ABC是等腰三角形的理由. D思路:作△ABC的角平分线AD 12G作∠BAC的角平分线AD,交BC于点D论证猜想如图,在△ABC中,已知∠B=∠C,说明△ABC是等腰三角形的理由. 思路:作△ABC的高AD
12DPF过点A作AD⊥BC于点D论证猜想如图,在△ABC中,已知∠B=∠C,说明△ABC是等腰三角形的理由. 思路:作△ABC的中线AD
DPF取BC中点D,连结AD想一想:这个思路可以吗?去掉这个限制条件还成立吗?等腰三角形的判定方法 如果一个三角形有两个角相等,那么这两个角所对的边也相等,这个三角形是等腰三角形 .(简称为“等角对等边”) 符号语言: ∵ ∠B=∠C (已知), ∴ AC=AB(等角对等边) . 即△ABC是等腰三角形练一练例题:如图,在△ABC中,∠ABC 的平分线BD交AC于点D,DE∥BC,说明DE=BE的理由。变式1如图,在△ABC中,DE=BE,DE∥BC,说明BD平分∠ABC的理由。变式2如图,在△ABC中,∠ABC 的平分线BD交AC于点D,DE=BE,说明DE∥BC的理由。变式3如图,在△ABC中,DE∥BC,BF平分∠ABC,FC平分∠ACB,说明DE=BD+CE。折纸实验如图,将一个长方形纸条进行折叠,当叠合部分是一个三角形且折叠后长方形的四个顶点都不在长方形内部时,这个三角形必是一个等腰三角形。变式如图,把长方形纸片ABCD延对角线BD翻折,泛着后的边BC’与AD交于点O,
(1)说明BF=DF;
(2)若AD=8,AB=6,
求△ABF的周长小 结一. 等腰三角形的判定方法:(1)等腰三角形的定义(2)等角对等边两边相等的三角形是等腰三角形.等腰三角形在同一个三角形中!!小 结二. 基本图形:1. “ 角平分线——平行线——等腰三角形”
定义:有两条边相等的三角形叫等腰三角形
2.等腰三角形有哪些性质?
等边对等角
等腰三角形三线合一
复习平行线的性质:两直线平行,内错角相等
平行线的判定:内错角相等,两直线平行
等腰三角形的性质:等边对等角
等腰三角形的判定:等角对等边猜一猜论证猜想如图,在△ABC中,已知∠B=∠C,说明△ABC是等腰三角形的理由. D思路:作△ABC的角平分线AD 12G作∠BAC的角平分线AD,交BC于点D论证猜想如图,在△ABC中,已知∠B=∠C,说明△ABC是等腰三角形的理由. 思路:作△ABC的高AD
12DPF过点A作AD⊥BC于点D论证猜想如图,在△ABC中,已知∠B=∠C,说明△ABC是等腰三角形的理由. 思路:作△ABC的中线AD
DPF取BC中点D,连结AD想一想:这个思路可以吗?去掉这个限制条件还成立吗?等腰三角形的判定方法 如果一个三角形有两个角相等,那么这两个角所对的边也相等,这个三角形是等腰三角形 .(简称为“等角对等边”) 符号语言: ∵ ∠B=∠C (已知), ∴ AC=AB(等角对等边) . 即△ABC是等腰三角形练一练例题:如图,在△ABC中,∠ABC 的平分线BD交AC于点D,DE∥BC,说明DE=BE的理由。变式1如图,在△ABC中,DE=BE,DE∥BC,说明BD平分∠ABC的理由。变式2如图,在△ABC中,∠ABC 的平分线BD交AC于点D,DE=BE,说明DE∥BC的理由。变式3如图,在△ABC中,DE∥BC,BF平分∠ABC,FC平分∠ACB,说明DE=BD+CE。折纸实验如图,将一个长方形纸条进行折叠,当叠合部分是一个三角形且折叠后长方形的四个顶点都不在长方形内部时,这个三角形必是一个等腰三角形。变式如图,把长方形纸片ABCD延对角线BD翻折,泛着后的边BC’与AD交于点O,
(1)说明BF=DF;
(2)若AD=8,AB=6,
求△ABF的周长小 结一. 等腰三角形的判定方法:(1)等腰三角形的定义(2)等角对等边两边相等的三角形是等腰三角形.等腰三角形在同一个三角形中!!小 结二. 基本图形:1. “ 角平分线——平行线——等腰三角形”
