14.6 等腰三角形的判定 课件(23张PPT)
文档属性
| 名称 | 14.6 等腰三角形的判定 课件(23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 290.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 17:35:56 | ||
图片预览








文档简介
课件23张PPT。14.6等腰三角形的判定 等腰三角形的性质: 复习回顾 (2) 等腰三角形的两个底角相等.
也就是说,在同一个三角形中,等边对等角; (3) 等腰三角形的顶角平分线、底边上的中线和
高互相重合, 简称等腰三角形的三线合一. (1)等腰三角形的两腰相等; (4) 等腰三角形是轴对称图形,对称轴是顶角的平
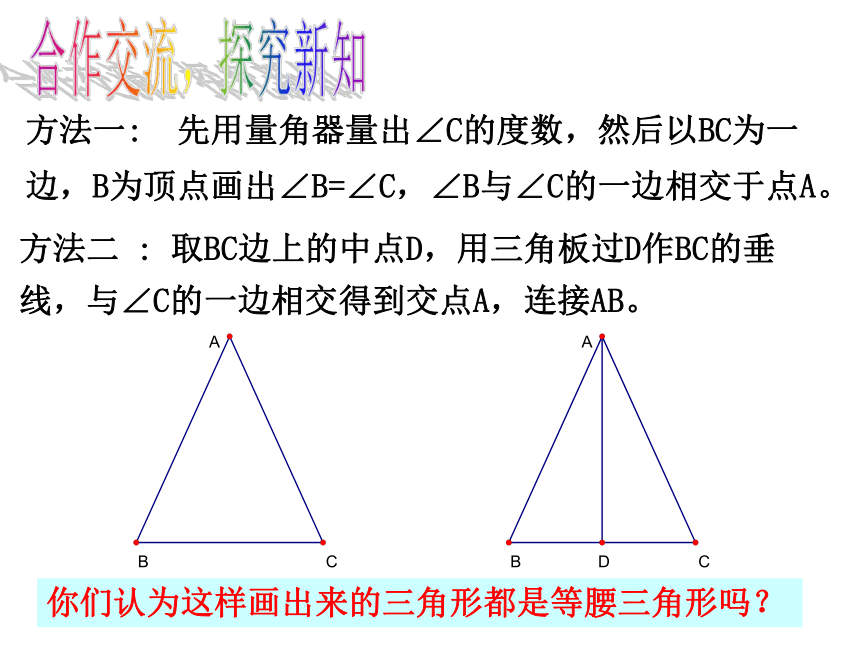
分线所在的直线。设置疑问,引出新课 下面有这样一个问题:如图,小明练习册上的一个⊿ABC是等腰三角形,AB=AC,它的一部分被墨迹污染了,只剩底边BC和∠C。有没有办法把原来的等腰三角形ABC重新画出来?合作交流,探究新知 方法一: 先用量角器量出∠C的度数,然后以BC为一边,B为顶点画出∠B=∠C,∠B与∠C的一边相交于点A。 方法二 : 取BC边上的中点D,用三角板过D作BC的垂线,与∠C的一边相交得到交点A,连接AB。 你们认为这样画出来的三角形都是等腰三角形吗?学习目标:1、理解等腰三角形的判定方法的证
明过程;
2、明确等腰三角形的判定方法并能
应用判定方法解决相关问题;
3、通过解决问题了解几何中的一些
基本 图形和规律并能试着应用。
分析第一种画法:已知:在△ABC中,∠B=∠C,说明△ABC是等腰三角形的理由。 要证明两条线段相等,常用什么方法? 添辅助线 解:作ΔABC的角平分线AD,交BC于点D,则 ∠1=∠2 (角平分线的意义)
在ΔABD和ΔACD中(已知)(已证)(公共边)∴ΔABD≌ΔACD(AAS)∴AB=AC 如果一个三角形有两个角相等,那么这个三角形是等腰三角形。简单地说,在同一个三角形中,等角对等边。(全等三角形的对应边相等)∴ΔABC是等腰三角形 已知在一个三角形中,等角对等边如果一个三角形有两个角相等,那么这个三角形是等腰三角形。 在△ABC中, ∵∠B=∠C ( ) ∴ AC=AB. ( )
∴ △ABC是等腰三角形用符号语言表示为:这又是一个判定两条线段相等根据之一.“在同一个三角形中,等角对等边。”2、如果一个三角形有两个角相等,那么这个三角形是等腰三角形.等腰三角形的判定方法:“在同一个三角形中, 等边对等角。”辨一辨:1、有两边相等的三角形是等腰三角形。反馈练习 1.在△ABC中, 已知∠A=50°,∠B=65°,判断△ABC是什么三角形,为什么?解:△ABC是等腰三角形, 因为∠B=65°, ∠A=50°, 所以∠C=65°, ∠B =∠C=65°2.如图,已知∠A=36°, ∠DBC=36°, ∠C=72°,则∠1= __,∠2= __, 图中的等腰三角形有 36°72°△ABC△DBA△BCD试一试:如图,在△ABC中,BD、CE分别是边AC,AB上的高,且CE=BD, 说明△ABC是等腰三角形的理由。 例1:如图,在△ABC中,BD、CE分别是边AC,AB上的高,且∠1=∠2, 说明△ABC是等腰三角形的理由。 如图,在△ABC中,D,E分别是AC,AB上的点,BD,CE相交于 点O。 BD=CE,若∠1=∠2,
问△ABC是等腰三角形吗?
请说明理由。练一练:如图,(1)已知:OD平分∠AOB,ED∥OA,求证:EO=ED。例2 :(2)已知:OD平分∠AOB,EO=ED。
求证:ED∥OA。
(3)已知:ED∥OA,EO=ED。求证:OD平分∠AOB。
练一练:如图,AD平分△ABC的外角∠EAC,AD//BC,则△ ABC是等腰三角形吗?说明你的理由。(1)如图c, BD平分∠ABC,CD平分∠ACB,过D作EF∥BC交AB于E,交AC于F,则图中有几个等腰三角形?还可证出哪些线段的 和差关系?
(2)已知:如图a,AB=AC,BD平分∠ABC,CD平分∠ACB,过D作EF∥BC交AB于E,交AC于F,则图中有几个等腰三角形?
(3)如图b,AB=AC,BF 平分∠ABC交AC于F,CE平分∠ACB交AB于E,BF和BE交于点D,且EF∥BC,则图中有几个等腰三角形?
已知:如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB并交于点O,过点O作 OD∥AB, OE∥AC,BC=16,
求: △ODE的周长有两边相等的三角形是等腰三角形2.等边对等角3. 三线合一4.是轴对称图形2.等角对等边1.两边相等1.两腰相等练习题:如图,△ABC中,∠B=∠C,BD=CE,说明∠1=∠2的理由ABCDE12思考:等腰三角形两个角相等两个角相等等腰三角形等腰三角形“三线合一”“三线合一”等腰三角形这个问题,我们作为今天的思考题,我们下节课继续讲解例:如图,BD是等腰三角形ABC的底边AC上的高,DE∥BC, 交AB于点E, 判断△BDE是不是等腰三角形? 例题
也就是说,在同一个三角形中,等边对等角; (3) 等腰三角形的顶角平分线、底边上的中线和
高互相重合, 简称等腰三角形的三线合一. (1)等腰三角形的两腰相等; (4) 等腰三角形是轴对称图形,对称轴是顶角的平
分线所在的直线。设置疑问,引出新课 下面有这样一个问题:如图,小明练习册上的一个⊿ABC是等腰三角形,AB=AC,它的一部分被墨迹污染了,只剩底边BC和∠C。有没有办法把原来的等腰三角形ABC重新画出来?合作交流,探究新知 方法一: 先用量角器量出∠C的度数,然后以BC为一边,B为顶点画出∠B=∠C,∠B与∠C的一边相交于点A。 方法二 : 取BC边上的中点D,用三角板过D作BC的垂线,与∠C的一边相交得到交点A,连接AB。 你们认为这样画出来的三角形都是等腰三角形吗?学习目标:1、理解等腰三角形的判定方法的证
明过程;
2、明确等腰三角形的判定方法并能
应用判定方法解决相关问题;
3、通过解决问题了解几何中的一些
基本 图形和规律并能试着应用。
分析第一种画法:已知:在△ABC中,∠B=∠C,说明△ABC是等腰三角形的理由。 要证明两条线段相等,常用什么方法? 添辅助线 解:作ΔABC的角平分线AD,交BC于点D,则 ∠1=∠2 (角平分线的意义)
在ΔABD和ΔACD中(已知)(已证)(公共边)∴ΔABD≌ΔACD(AAS)∴AB=AC 如果一个三角形有两个角相等,那么这个三角形是等腰三角形。简单地说,在同一个三角形中,等角对等边。(全等三角形的对应边相等)∴ΔABC是等腰三角形 已知在一个三角形中,等角对等边如果一个三角形有两个角相等,那么这个三角形是等腰三角形。 在△ABC中, ∵∠B=∠C ( ) ∴ AC=AB. ( )
∴ △ABC是等腰三角形用符号语言表示为:这又是一个判定两条线段相等根据之一.“在同一个三角形中,等角对等边。”2、如果一个三角形有两个角相等,那么这个三角形是等腰三角形.等腰三角形的判定方法:“在同一个三角形中, 等边对等角。”辨一辨:1、有两边相等的三角形是等腰三角形。反馈练习 1.在△ABC中, 已知∠A=50°,∠B=65°,判断△ABC是什么三角形,为什么?解:△ABC是等腰三角形, 因为∠B=65°, ∠A=50°, 所以∠C=65°, ∠B =∠C=65°2.如图,已知∠A=36°, ∠DBC=36°, ∠C=72°,则∠1= __,∠2= __, 图中的等腰三角形有 36°72°△ABC△DBA△BCD试一试:如图,在△ABC中,BD、CE分别是边AC,AB上的高,且CE=BD, 说明△ABC是等腰三角形的理由。 例1:如图,在△ABC中,BD、CE分别是边AC,AB上的高,且∠1=∠2, 说明△ABC是等腰三角形的理由。 如图,在△ABC中,D,E分别是AC,AB上的点,BD,CE相交于 点O。 BD=CE,若∠1=∠2,
问△ABC是等腰三角形吗?
请说明理由。练一练:如图,(1)已知:OD平分∠AOB,ED∥OA,求证:EO=ED。例2 :(2)已知:OD平分∠AOB,EO=ED。
求证:ED∥OA。
(3)已知:ED∥OA,EO=ED。求证:OD平分∠AOB。
练一练:如图,AD平分△ABC的外角∠EAC,AD//BC,则△ ABC是等腰三角形吗?说明你的理由。(1)如图c, BD平分∠ABC,CD平分∠ACB,过D作EF∥BC交AB于E,交AC于F,则图中有几个等腰三角形?还可证出哪些线段的 和差关系?
(2)已知:如图a,AB=AC,BD平分∠ABC,CD平分∠ACB,过D作EF∥BC交AB于E,交AC于F,则图中有几个等腰三角形?
(3)如图b,AB=AC,BF 平分∠ABC交AC于F,CE平分∠ACB交AB于E,BF和BE交于点D,且EF∥BC,则图中有几个等腰三角形?
已知:如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB并交于点O,过点O作 OD∥AB, OE∥AC,BC=16,
求: △ODE的周长有两边相等的三角形是等腰三角形2.等边对等角3. 三线合一4.是轴对称图形2.等角对等边1.两边相等1.两腰相等练习题:如图,△ABC中,∠B=∠C,BD=CE,说明∠1=∠2的理由ABCDE12思考:等腰三角形两个角相等两个角相等等腰三角形等腰三角形“三线合一”“三线合一”等腰三角形这个问题,我们作为今天的思考题,我们下节课继续讲解例:如图,BD是等腰三角形ABC的底边AC上的高,DE∥BC, 交AB于点E, 判断△BDE是不是等腰三角形? 例题
