两边相等问题 课件(11张PPT)
文档属性
| 名称 | 两边相等问题 课件(11张PPT) | 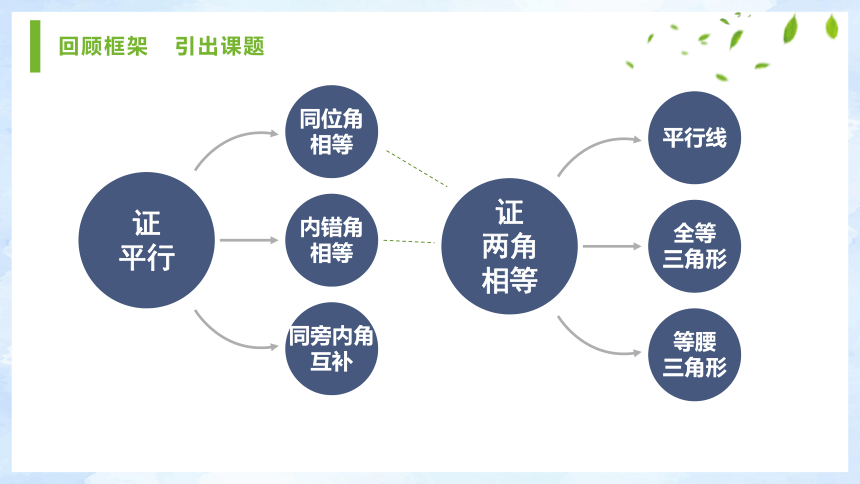 | |
| 格式 | zip | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 18:02:42 | ||
图片预览




文档简介
课件12张PPT。回顾框架 引出课题证
平行同位角
相等内错角
相等同旁内角
互补证
两角
相等平行线全等
三角形等腰
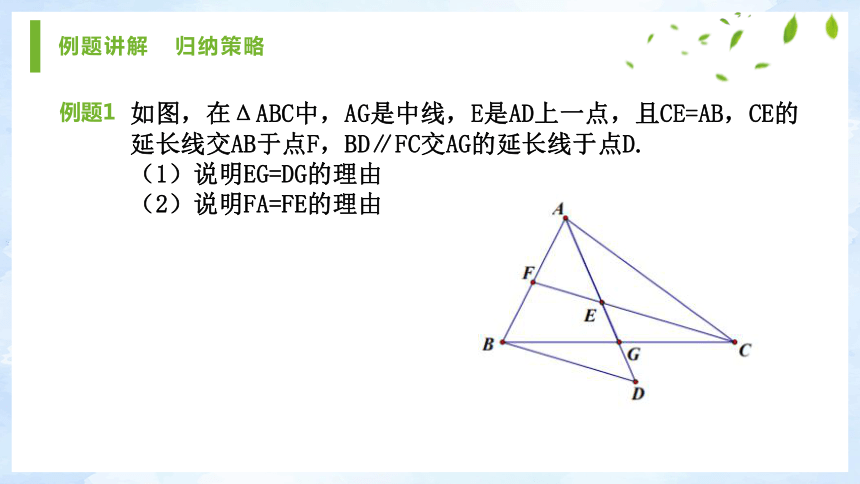
三角形三角形复两相等问题习边题组复习 初现策略1.如图,已知?ABD≌?DCA,A和D,C和B分别是对应点,如果AB=7cm,AD=6cm,BD=4cm,则DC= .2.如图,在△ABC中,若∠C=90o,BD平分∠ABC,DE⊥AB,则图中与线段DC相等的线段是________ . 7cmDE4.在等腰三角形ABC中,AB = 6cm,BC = 10cm,那AC=_________cm.5.在?ABC中,若∠A=80o,∠B=50o,AC=5,则AB=_________.6或1053.如图,已知△ABC≌?DEF,若BC=5,EC=3,则CF=________ . 26.如图,在等腰三角形中,AB=AC,AD⊥BC,BC=8,则BD=_________.4例题讲解 归纳策略例题1如图,在ΔABC中,AG是中线,E是AD上一点,且CE=AB,CE的延长线交AB于点F,BD∥FC交AG的延长线于点D.
(1)说明EG=DG的理由
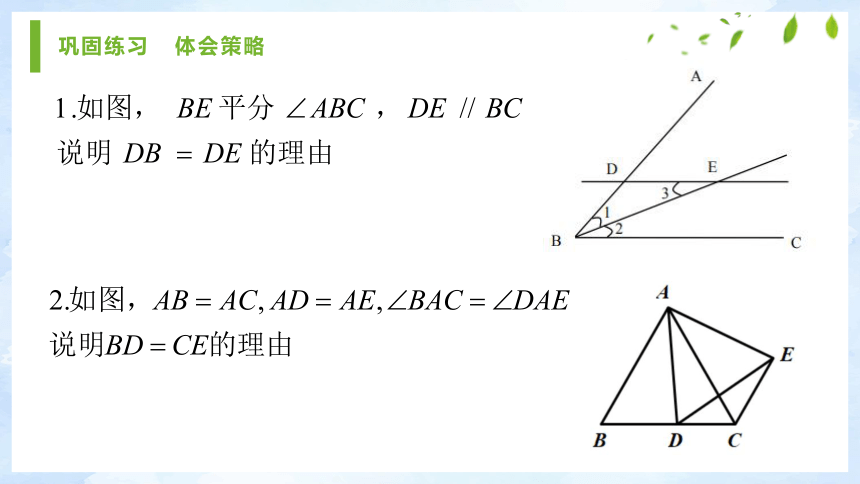
(2)说明FA=FE的理由所求两边在同一个三角形中,则采用证明此三角形为等腰三角形的方式来说明两边相等。所求两边分别在两个不同的三角形中,则采用证明这两个三角形全等的方式来说明两边相等。说明两边相等的策略小结1.全等三角形2.等腰三角形巩固练习 体会策略补齐框架 重现策略证
平行同位角
相等内错角
相等同旁内角
互补证
两角
相等全等
三角形等腰
三角形平行线证
两边
相等变式提升 综合策略变式1:如图,已知?ABC为等边三角形,点D为直线BC上的一个动点,
不与点B,C重合,以AD为边作等边?ADE,顶点A,D,E按逆时针方向排列,连接CE.说明BD=CE的理由.
当点D在边BC上时,变式提升 综合策略变式2:如图,已知?ABC为等边三角形,点D为直线BC上的一个动点,
不与点B,C重合,以AD为边作等边?ADE,顶点A,D,E按逆时针方向排列,连接CE.说明BD=CE的理由.
当点D在边BC的延长线上时,变式提升 综合策略变式3:如图,已知?ABC为等边三角形,点D为直线BC上的一个动点,
不与点B,C重合,以AD为边作等边?ADE,顶点A,D,E按逆时针方向排列,连接CE.说明BD=CE的理由.
当点D在边BC的反向延长线上时,变式提升 综合策略变式4:如图,已知?ABC为等边三角形,点D为直线BC上的一个动点,
不与点B,C重合,以AD为边作等边?ADE,顶点A,D,E按逆时针方向排列,连接CE.说明BD=CE的理由.
课堂总结1.你巩固了哪些知识点?
2.你收获了哪些解题方法?
3.你领悟了哪些数学思想?
平行同位角
相等内错角
相等同旁内角
互补证
两角
相等平行线全等
三角形等腰
三角形三角形复两相等问题习边题组复习 初现策略1.如图,已知?ABD≌?DCA,A和D,C和B分别是对应点,如果AB=7cm,AD=6cm,BD=4cm,则DC= .2.如图,在△ABC中,若∠C=90o,BD平分∠ABC,DE⊥AB,则图中与线段DC相等的线段是________ . 7cmDE4.在等腰三角形ABC中,AB = 6cm,BC = 10cm,那AC=_________cm.5.在?ABC中,若∠A=80o,∠B=50o,AC=5,则AB=_________.6或1053.如图,已知△ABC≌?DEF,若BC=5,EC=3,则CF=________ . 26.如图,在等腰三角形中,AB=AC,AD⊥BC,BC=8,则BD=_________.4例题讲解 归纳策略例题1如图,在ΔABC中,AG是中线,E是AD上一点,且CE=AB,CE的延长线交AB于点F,BD∥FC交AG的延长线于点D.
(1)说明EG=DG的理由
(2)说明FA=FE的理由所求两边在同一个三角形中,则采用证明此三角形为等腰三角形的方式来说明两边相等。所求两边分别在两个不同的三角形中,则采用证明这两个三角形全等的方式来说明两边相等。说明两边相等的策略小结1.全等三角形2.等腰三角形巩固练习 体会策略补齐框架 重现策略证
平行同位角
相等内错角
相等同旁内角
互补证
两角
相等全等
三角形等腰
三角形平行线证
两边
相等变式提升 综合策略变式1:如图,已知?ABC为等边三角形,点D为直线BC上的一个动点,
不与点B,C重合,以AD为边作等边?ADE,顶点A,D,E按逆时针方向排列,连接CE.说明BD=CE的理由.
当点D在边BC上时,变式提升 综合策略变式2:如图,已知?ABC为等边三角形,点D为直线BC上的一个动点,
不与点B,C重合,以AD为边作等边?ADE,顶点A,D,E按逆时针方向排列,连接CE.说明BD=CE的理由.
当点D在边BC的延长线上时,变式提升 综合策略变式3:如图,已知?ABC为等边三角形,点D为直线BC上的一个动点,
不与点B,C重合,以AD为边作等边?ADE,顶点A,D,E按逆时针方向排列,连接CE.说明BD=CE的理由.
当点D在边BC的反向延长线上时,变式提升 综合策略变式4:如图,已知?ABC为等边三角形,点D为直线BC上的一个动点,
不与点B,C重合,以AD为边作等边?ADE,顶点A,D,E按逆时针方向排列,连接CE.说明BD=CE的理由.
课堂总结1.你巩固了哪些知识点?
2.你收获了哪些解题方法?
3.你领悟了哪些数学思想?
