第十四章 第二节 全等三角形的复习与探究 课件(21张PPT)
文档属性
| 名称 | 第十四章 第二节 全等三角形的复习与探究 课件(21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 208.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-09 00:00:00 | ||
图片预览



文档简介
课件21张PPT。全等三角形复习与探究知识回顾一、全等三角形概念:
能够 的三角形是全等三角形. 二、全等三角形性质:
全等三角形对应边 .
全等三角形对应角 .重合相等相等知识回顾三、判定两个三角形全等的条件:
S. S. SS. A. SA. S. AA. A. S注意:
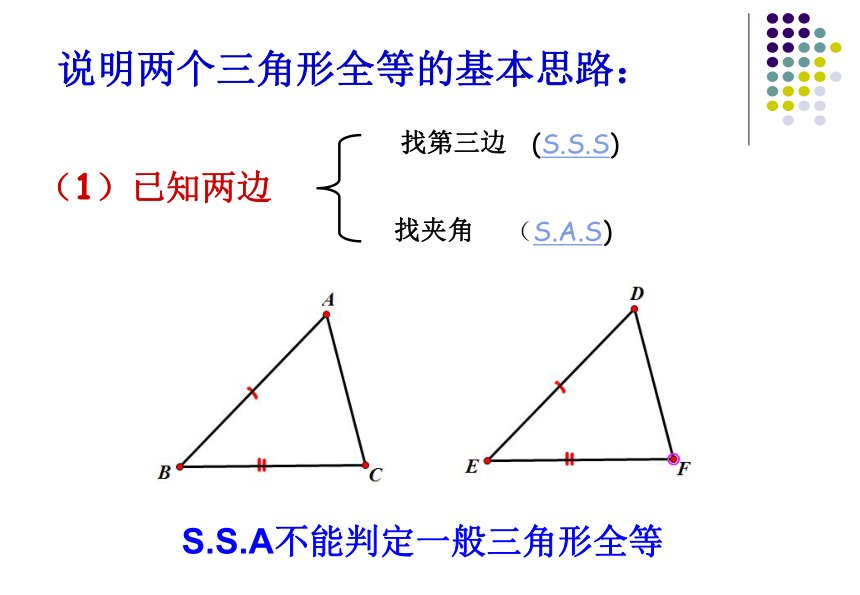
______________不能判断一般三角形全等.A.A.A , S.S.A说明两个三角形全等的基本思路:(1)已知两边 找第三边(S.S.S)找夹角(S.A.S)S.S.A不能判定一般三角形全等说明两个三角形全等的基本思路: (2) 已知一边一角已知一边和它的邻角已知一边和它的对角
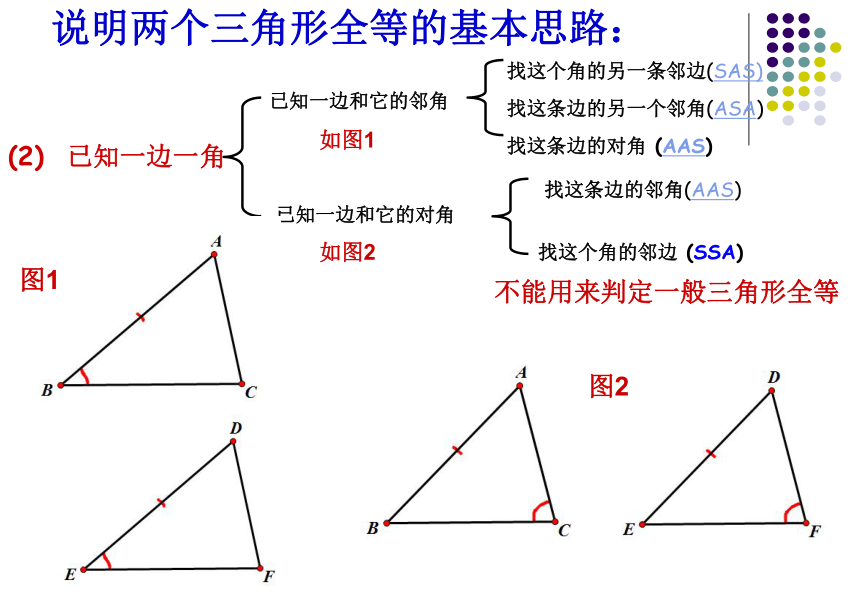
找这条边的另一个邻角(ASA)找这个角的另一条邻边(SAS)找这个角的邻边 (SSA)
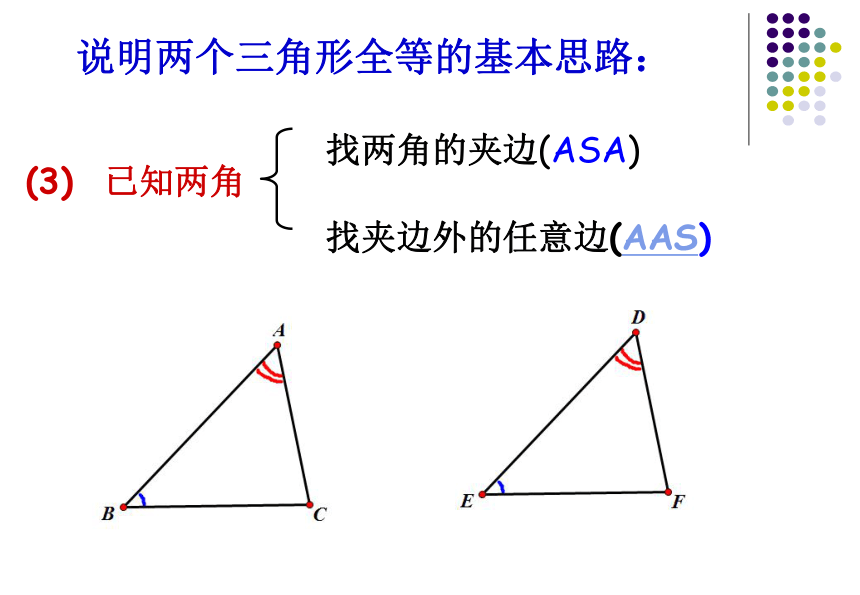
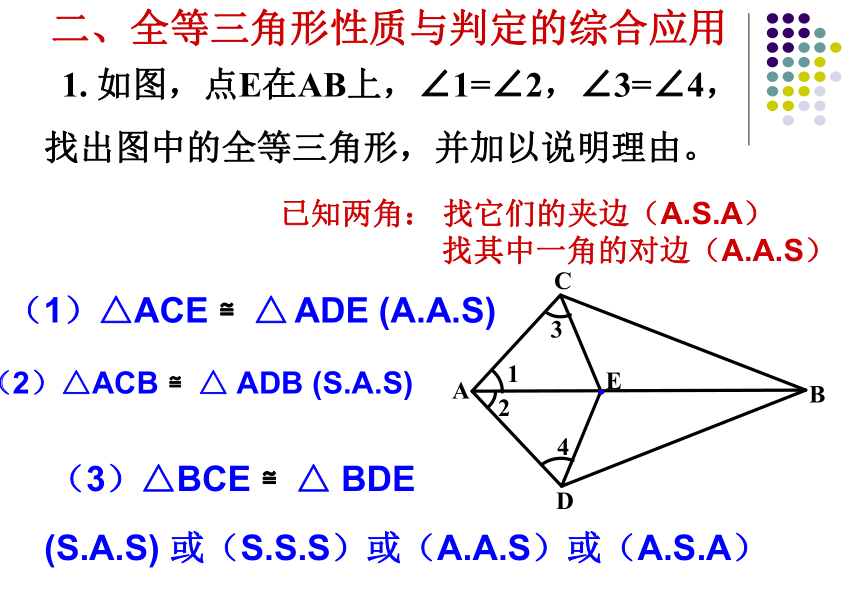
找这条边的邻角(AAS)图1图2如图1如图2找这条边的对角 (AAS)不能用来判定一般三角形全等说明两个三角形全等的基本思路:(3) 已知两角找两角的夹边(ASA)找夹边外的任意边(AAS)二、全等三角形性质与判定的综合应用(1)△ACE ≌△ ADE (A.A.S)(2)△ACB ≌△ ADB (S.A.S)(3)△BCE ≌△ BDE(S.A.S) 或(S.S.S)或(A.A.S)或(A.S.A)
已知两角: 找它们的夹边(A.S.A)
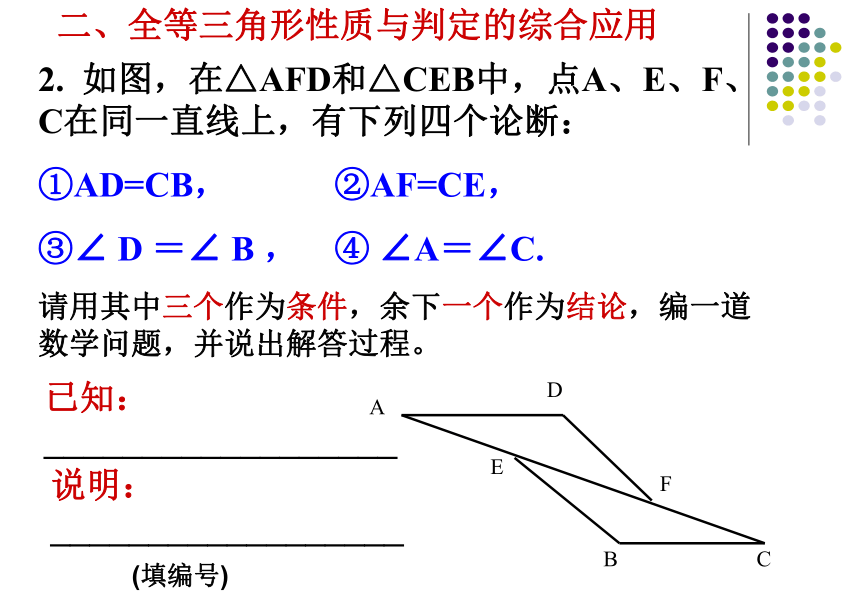
找其中一角的对边(A.A.S)2. 如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,有下列四个论断:
①AD=CB, ②AF=CE,
③∠ D =∠ B , ④ ∠A=∠C.
请用其中三个作为条件,余下一个作为结论,编一道数学问题,并说出解答过程。二、全等三角形性质与判定的综合应用已知:__________________说明:__________________(填编号)如图,在△ABC和△BAD中,AC = BD,
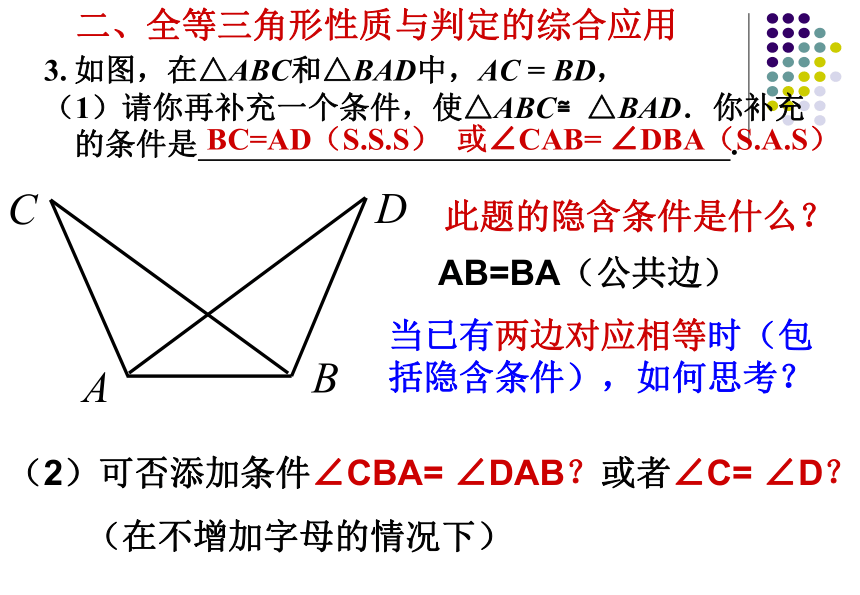
(1)请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 .BC=AD(S.S.S)或∠CAB= ∠DBA(S.A.S)当已有两边对应相等时(包括隐含条件),如何思考?(2)可否添加条件∠CBA= ∠DAB?或者∠C= ∠D?
(在不增加字母的情况下)
二、全等三角形性质与判定的综合应用此题的隐含条件是什么?AB=BA(公共边)如图,在△ABC和△BAD中,AC = BD,(3)增加点O后,已知AC = BD的条件不变,请补充一个条件,使△AOC≌△BOD.你补充的条件是 .O∠C=∠D(A.A.S)或∠CAO=∠DBO(A.A.S)(4)增加的条件可否是: BC=AD
或∠CAB= ∠DBA?
当已有“一边和这边对角对应相等”时,如何思考?二、全等三角形性质与判定的综合应用此题的隐含条件是什么?∠AOC= ∠BOD(对顶角相等)方法 规律 总结全等三角形是说明两条线段或两个角相等的重要方法之一,说明时
①要观察待说明的线段或角:在哪两个可能全等的三角形中。
②要说明两个三角形全等的思路:题目给的直接条件是什么?图形的隐含条件是什么?需要说明的间接条件是什么?1、两个大小不同的等腰直角三角板摆放成如图1所示的情况,图2是由它抽象出的几何图形,B、C、E在同一条直线上,联结BE、DC。
(1)请找出图2中的全等三角形,并说明理由。
(结论中不得含有未标识的字母)图1三、图形变化中探究全等三角形图2△ABE ≌ △ ACD(2)猜想并说明CD和BE的关系
结论:CD=BE结论:CD⊥BE两条线段的关系:
既指数量关系,
又指位置关系。
(两条线段所在的直线)2、如图3:已知等腰直角三角形ABC,将等腰直角三角形ADE绕点A顺时针旋转一定角度,B、C、D在同一条直线上,联结BE、DC。猜想并说明CD和BE的关系
图3线段BE与CD不相交,
但所在的直线会垂直,
结论:CD=BE结论:CD⊥BE3、如图4:已知等腰直角三角形ABC,将等腰直角三角形ADE绕点A逆时针旋转一定角度,B、C、E不在同一条直线上,联结BE、DC。猜想并说明CD和BE的关系
图4结论:CD=BE结论:CD⊥BE4、如图5、图6:已知△ABC和△ ADE都是等边三角形。猜想并说明CD和BE的关系
图5图6结论:CD=BE结论:CD⊥BE还成立吗?直线CD与BE相交的夹角______度?60 在前面几题的前提下: 若把△ABC 与△ADE的形状改变成任意三角形,则CD与BE的数量关系和位置关系还成立吗?如果要成立的话,则△ABC 与△ADE必须满足怎样的条件?等腰三角形 + 一角对应相等课堂小结通过刚才的学习,
你有哪些收获?1、公共角、公共边、对顶角,是说明中常用的条件。 (图中的隐含条件) 2、线段的和差、角的和差,是说明中常用的方法。
(等式性质)
3、两次全等:第一对全等三角形为第二对全等三角形创造条件。说明两个三角形全等的基本思路:(1)已知两边---- 找第三边(SSS)找夹角(SAS)(2) 已知一边一角---已知一边和它的邻角已知一边和它的对角 ----
找这边的另一个邻角(ASA)找这个角的另一个边(SAS)找这边的对角 (AAS)找一角(AAS)(3) 已知两角---找两角的夹边(ASA)找夹边外的任意边(AAS)布置作业1、生态作业:P70—71页2、练习册:P53—54页
P64页
能够 的三角形是全等三角形. 二、全等三角形性质:
全等三角形对应边 .
全等三角形对应角 .重合相等相等知识回顾三、判定两个三角形全等的条件:
S. S. SS. A. SA. S. AA. A. S注意:
______________不能判断一般三角形全等.A.A.A , S.S.A说明两个三角形全等的基本思路:(1)已知两边 找第三边(S.S.S)找夹角(S.A.S)S.S.A不能判定一般三角形全等说明两个三角形全等的基本思路: (2) 已知一边一角已知一边和它的邻角已知一边和它的对角
找这条边的另一个邻角(ASA)找这个角的另一条邻边(SAS)找这个角的邻边 (SSA)
找这条边的邻角(AAS)图1图2如图1如图2找这条边的对角 (AAS)不能用来判定一般三角形全等说明两个三角形全等的基本思路:(3) 已知两角找两角的夹边(ASA)找夹边外的任意边(AAS)二、全等三角形性质与判定的综合应用(1)△ACE ≌△ ADE (A.A.S)(2)△ACB ≌△ ADB (S.A.S)(3)△BCE ≌△ BDE(S.A.S) 或(S.S.S)或(A.A.S)或(A.S.A)
已知两角: 找它们的夹边(A.S.A)
找其中一角的对边(A.A.S)2. 如图,在△AFD和△CEB中,点A、E、F、C在同一直线上,有下列四个论断:
①AD=CB, ②AF=CE,
③∠ D =∠ B , ④ ∠A=∠C.
请用其中三个作为条件,余下一个作为结论,编一道数学问题,并说出解答过程。二、全等三角形性质与判定的综合应用已知:__________________说明:__________________(填编号)如图,在△ABC和△BAD中,AC = BD,
(1)请你再补充一个条件,使△ABC≌△BAD.你补充的条件是 .BC=AD(S.S.S)或∠CAB= ∠DBA(S.A.S)当已有两边对应相等时(包括隐含条件),如何思考?(2)可否添加条件∠CBA= ∠DAB?或者∠C= ∠D?
(在不增加字母的情况下)
二、全等三角形性质与判定的综合应用此题的隐含条件是什么?AB=BA(公共边)如图,在△ABC和△BAD中,AC = BD,(3)增加点O后,已知AC = BD的条件不变,请补充一个条件,使△AOC≌△BOD.你补充的条件是 .O∠C=∠D(A.A.S)或∠CAO=∠DBO(A.A.S)(4)增加的条件可否是: BC=AD
或∠CAB= ∠DBA?
当已有“一边和这边对角对应相等”时,如何思考?二、全等三角形性质与判定的综合应用此题的隐含条件是什么?∠AOC= ∠BOD(对顶角相等)方法 规律 总结全等三角形是说明两条线段或两个角相等的重要方法之一,说明时
①要观察待说明的线段或角:在哪两个可能全等的三角形中。
②要说明两个三角形全等的思路:题目给的直接条件是什么?图形的隐含条件是什么?需要说明的间接条件是什么?1、两个大小不同的等腰直角三角板摆放成如图1所示的情况,图2是由它抽象出的几何图形,B、C、E在同一条直线上,联结BE、DC。
(1)请找出图2中的全等三角形,并说明理由。
(结论中不得含有未标识的字母)图1三、图形变化中探究全等三角形图2△ABE ≌ △ ACD(2)猜想并说明CD和BE的关系
结论:CD=BE结论:CD⊥BE两条线段的关系:
既指数量关系,
又指位置关系。
(两条线段所在的直线)2、如图3:已知等腰直角三角形ABC,将等腰直角三角形ADE绕点A顺时针旋转一定角度,B、C、D在同一条直线上,联结BE、DC。猜想并说明CD和BE的关系
图3线段BE与CD不相交,
但所在的直线会垂直,
结论:CD=BE结论:CD⊥BE3、如图4:已知等腰直角三角形ABC,将等腰直角三角形ADE绕点A逆时针旋转一定角度,B、C、E不在同一条直线上,联结BE、DC。猜想并说明CD和BE的关系
图4结论:CD=BE结论:CD⊥BE4、如图5、图6:已知△ABC和△ ADE都是等边三角形。猜想并说明CD和BE的关系
图5图6结论:CD=BE结论:CD⊥BE还成立吗?直线CD与BE相交的夹角______度?60 在前面几题的前提下: 若把△ABC 与△ADE的形状改变成任意三角形,则CD与BE的数量关系和位置关系还成立吗?如果要成立的话,则△ABC 与△ADE必须满足怎样的条件?等腰三角形 + 一角对应相等课堂小结通过刚才的学习,
你有哪些收获?1、公共角、公共边、对顶角,是说明中常用的条件。 (图中的隐含条件) 2、线段的和差、角的和差,是说明中常用的方法。
(等式性质)
3、两次全等:第一对全等三角形为第二对全等三角形创造条件。说明两个三角形全等的基本思路:(1)已知两边---- 找第三边(SSS)找夹角(SAS)(2) 已知一边一角---已知一边和它的邻角已知一边和它的对角 ----
找这边的另一个邻角(ASA)找这个角的另一个边(SAS)找这边的对角 (AAS)找一角(AAS)(3) 已知两角---找两角的夹边(ASA)找夹边外的任意边(AAS)布置作业1、生态作业:P70—71页2、练习册:P53—54页
P64页
