北师大版八年级数学上册 第二章 实数复习课课件(共42张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 第二章 实数复习课课件(共42张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
第二章 实数
复习回顾
兴宁市大坪中学 练小盛
1.熟练掌握算术平方根,平方根,立方根的相关概念.
2.熟练掌握无理数的概念,会对一个无理数进行估算.
3.掌握实数的定义,能熟练地进行实数的化简和计算.
学习目标:
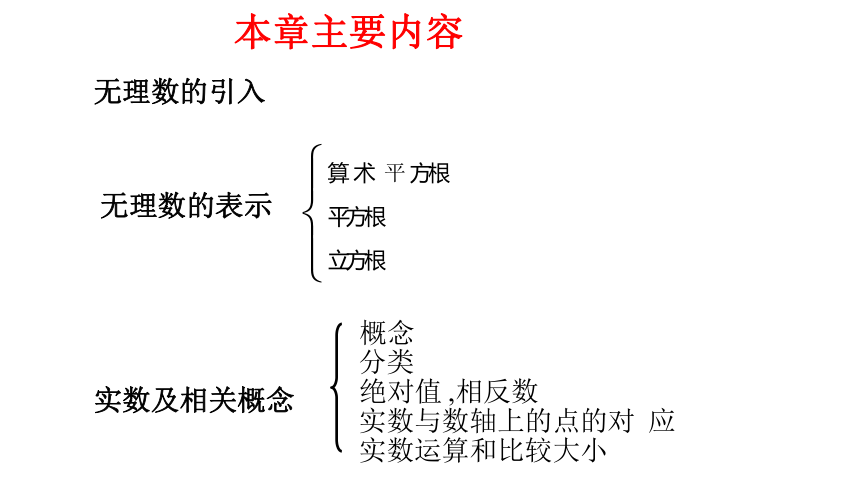
本章主要内容
实数及相关概念
无理数的引入
无理数的表示
一、复习回顾
1、无理数的定义:
无限不循环小数叫做无理数
2、有理数的定义:
有限和无限循环小数叫做有理数
或整数与分数统称为有理数
3.算术平方根的定义及性质
定义:一个 正数x 的平方等于a,则 x 叫 a 的 算术平方根. 记作:X = (a≥0)
0的算术平方根是0.
因为 表示 a 的算术平方根,
所以 ≥0 (a≥0)
4.平方根的定义及性质
定义:一个数 x 的平方等于a,即x2=a,则 x 叫 a 的平方根. 记作: X= (a≥0)
0的平方根是0.
性质:
一个正数有两个平方根,它们互为相反数.
0的平方根是0.
负数没有平方根.
定义:一个数 x 的立方等于a,即x3=a,则 x 叫 a 的立方根. 记作: X=
0的立方根是0.
5.立方根的定义及性质
性质:
一个正数有一个正的立方根,
一个负数有一个负的立方根.
0的立方根是0.
6.实数的定义及实数的运算法则
定义:有理数和无理数统称实数.
分类:
(按定义分) (按大小分)
有理数 正实数
实数 实数 0
无理数 负实数
实数与数轴上的点一一对应,实数可以比较大小.
实数有相反数,倒数,绝对值.有理数的运算法则和运算律
在实数范围内仍然适用.
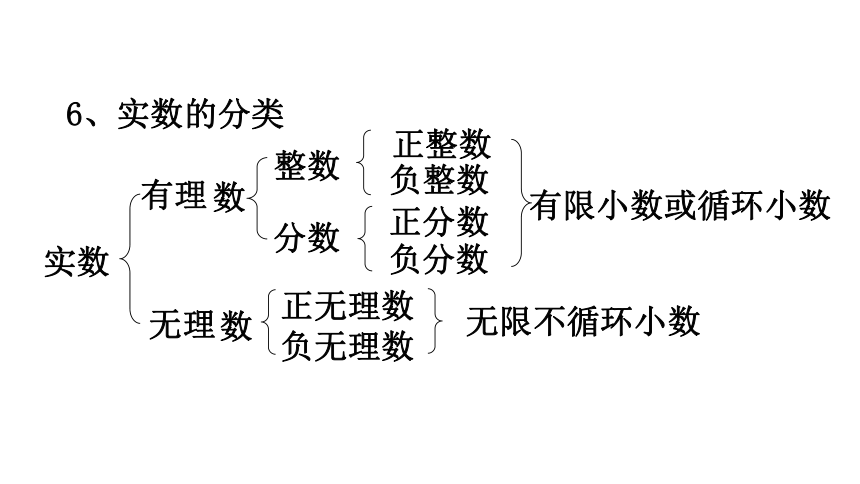
6、实数的分类
实数
数
数
整数
分数
正整数
负整数
负分数
正分数
正无理数
负无理数
有限小数或循环小数
无限不循环小数
有理
无理
7、实数的性质:
在实数范围内,相反数、倒数、
绝对值的意义和有理数的相反数、倒数、绝对值的意义完全一样。
例如:
是一个实数,它的相反数为 ;
绝对值为 .如果 那么它的
倒数为 .
1
7、实数的性质:
在实数范围内,相反数、倒数、
绝对值的意义和有理数的相反数、倒数、绝对值的意义完全一样。
>0)
反之
(a≥0,b>0)
8.无理数的乘除法则
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
结合所学知识,完成下表:
9.每个实数都可以用数轴上的
一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上点是一一对应的.
同样,在数轴上,右边的点表示的数比左边的点表示的数大.
数轴上一个点
有一个实数
点 数
有一个实数
数轴上一个点
数 点
要点、考点聚焦
1.几个重要的运算律:
(1)加法的交换律:a+b=b+a
(2)加法的结合律:(a+b)+c=a+(b+c)
(3)乘法的交换律:ab=ba
(4)加法的结合律:(ab)c=a(bc)
(5)乘法对加法的分配律:a(b+c)=ab+ac
2.实数的运算主要有:加、减、乘、除、乘方、开方.实数的运算顺序:先乘方、开方,再乘、除,最后算加、减,有括号的先算括号里面的.
3.科学记数法的一般形式为:a×10n(1≤a≤10,n为整数).
4.有效数字是指一个数从左边第一个不为零的数字起到右边所有的数字.
复习题
1.把下列各数写入相应的集合中:,0.3,,,
0,0.5757757775(相邻两个5之间7的个数逐次加1).
(1)正数集合
(2)负数集合
(3)有理数集合
(4)无理数集合
,0.3, , , 0.5757757775
,
,0.3, ,
, , 0.5757757775
2.求下列各数的平方根和算术平方根。
(1)2.25;(2)361;(3);(4)
解:(1)∵
∴
即2.25的平方根是,算术平方根是1.5
(2)∵
∴
即361的平方根是,算术平方根是19
2.求下列各数的平方根和算术平方根。
(1)2.25;(2)361;(3);(4)
解:(3)∵
∴
即的平方根是,算术平方根是
(4)∵
∴
即的平方根是,算术平方根是
3.求下列各数的立方根:
(1)512;(2)0.008:;(3);(4)
解:(1)∵
∴
(2)∵
∴
(3)∵
∴
(4)∵
∴
4.求下列各式的值:
(1);(2);(3);
(4);(5);(6)
(1)解:原式
(2)解:原式
(3)解:原式
(4)解:原式
(5)解:原式
(6)解:原式
5.用计算器求下列各式的值(结果精确到0.01):
(1);(2);(3);
(4);(5)
解:(1)
(2)
(3)
(4)
(5)
6.估算下列各数的大小:
(1)(结果精确到0.1);(2)(结果精确到1)
解:(1)∵4
∴6.6
∴
(2)∵6
∴4
∴
7.比较下列各组数的大小:
(1),1;(2);(3)
解:(1)∵ =1.5,
∴ 1
(2)∵ , 1.414
∴
(3)∵ ,
∴
8.计算:
(1);(2);(3)()()
(4)2;(5);(6)
(1)解:原式=
=32
=1
(2)解:原式=
=5
(3)解:原式=
=32
=1
(4)解:原式=2
=4
=16
8.计算:
(1);(2);(3)()()
(4)2;(5);(6)
(5)解:原式=
=
(6)解:原式=4
=
9.求代数式
(1)
解:(1)把代入中,得
原式=
=
=4
解:(2)将代入中,得
原式=
=
=2
10.如图,已知OA=OB。
(1)说出数轴上点A所表示的数;
(2)比较点A所表示的数与-2.5的大小。
-3
-2
-1
0
1
1
A
B
解:(1)点A表示
(2)∵
又∵6.25
∴6.255
∴
11.如图,在长方形ABCD中,∠DAE=∠CBE=45
求面积和周长(结果精确到0.01)
A
B
C
D
E
解:∵长方形ABCD中,∠D=90,∠DAE=45,AD=1
∴∠AED=45,DE=AD=1
同理可得∠BEC=45,CE=1
∴∠AEB=180,AE=BE=
∴=1,AB=
∴2+2
12.在数轴上找出表示下列各数的点:
解:如图,点D就是所要表示的点。
0
1
2
3
4
1
B
A
C
D
12.在数轴上找出表示下列各数的点:
解:如图,点B就是所要表示的点。
0
1
2
3
4
2
B
A
12.在数轴上找出表示下列各数的点:
解:如图,点B就是所要表示的点。
0
1
2
3
4
B
A
13. 1,2,3,4,5,6,7,8,9,10,的平方根和立方根中,哪些是有理数?
哪些是无理数?
解:1,2,3,4,5,6,7,8,9,10的平方根分别是±1,±, ±,
±2,±, ±, ±3, ±.
1,2,3,4,5,6,7,8,9,10的立方根分别是1,, , ,
, 2, 。
有理数有±1, ±2, ±3,1,2
无理数有±, ±, ±, ±,±,
, , , , 。
14.填空题:
(1)一个数的平方等于它本身,这个数是 ;
(2)平方根等于本身的数是 ;
(3)算术平方根等于本身的数是 ;
(4)立方根等于本身的数是 ;
(5)大于0且小于的整数是 ;
(6)满足整数是 ;
0,1
0
0,1
0,±1
1,2,3
1,0,1,2
15.判断题:
(1)不带根号的数都是有理数; ( )
(2)两个无理数的和还是无理数。 ( )
?
?
16.“无理数就是开方开不尽的数”这句话对吗?请举例说明。
答:不对。如无理数等是无理数,但不是开方开不尽的数。
17.如图,每个小正方形的边长为1,剪一剪,并拼成一个正方形,
这个正方形的边长是多少?
答:边长是。
18.一个圆的半径为1cm,和它等面积的正方形的边长是多少厘米?
(结果精确到0.01cm)
解:设正方形的边长为cm,依题意,得
答:正方形的边长约为1.77厘米。
19.一个正方体形状的木箱容积是4,求此木箱的棱长(结果精确到0.1m).
解:设木箱的棱长为m,依题意,得
答:木箱的棱长约为1.6米。
20.一个篮球的体积为9850c,求该篮球的半径r
(3.14,结果精确到0.1cm).
解:
=
r
答:该篮球的半径约为13.3cm。
21.一个长方形的长与宽的比是5:3,它的对角线长为cm,求这个长方形的长与宽(结果精确到0.1cm).
解:设长方形的长为5cm,宽为3cm,依题意,得
解得x=
所以57.1cm,34.2cm
答:长方形的长约为7.1厘米,宽约为4.2厘米。
22.设一个三角形的三边依次为a,b,c,p=(a+b+c),则有下列面积公式:S=
S=(秦九韶公式)
(1)一个三角形的三边长依次为5,6,7,利用两个公式分别求这个三角形的面积.
(2)一个三角形的三边长依次为,利用两个公式分别求这个三角形的面积.
解:(1)∵P==9
∴海伦公式S==
秦九韶公式S==6
22.设一个三角形的三边依次为a,b,c,p=(a+b+c),则有下列面积公式:S= S=(秦九韶公式)
(1)一个三角形的三边长依次为5,6,7,利用两个公式分别求这个三角形的面积.
(2)一个三角形的三边长依次为,利用两个公式分别求这个三角形的面积.
解:(2)∵P=
∴S=
=
秦九韶公式S=
=
23.座钟的摆钟摆动一个来回所需的时间称为一个周期,其计算公式
T=2,其中T表示周期(单位:s),l表示摆长(单位:m),取3.14,
g=9.8m/.假如一台座钟的摆长伟0.5m,它每摆动一个来回发出一次滴
答声,那么在1min内,该座钟大约发出了多少次滴答声。
解:把,g=9.8m/,=0.5m代入T=2中,得
T=2 次
答:该座钟大约发出了42次滴答声。
24.交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度,所用的
经验公式是=16,其中v表示车速(单位:km/h),d表示刹车后车轮滑过
的距离(单位:m),f表示摩擦因数。在某次交通事故调查中,测得
d=20m,f=1.2,肇事汽车的车速大约是多少?(结果精确到0.1km/h)
解:把d=20m,f=1.2代入=16中,得
V16=16
答:肇事汽车的车速大约是78.4km/h
25.用电器的电阻R、功率P与它两端的电压U之间有关系:P=.有两个外观
完全相同的用电器,甲的电阻伟18.4Ω,乙的电阻伟20.8Ω。现测得某电器
的功率为1500W,两端电压在150~170V,该用电器到底是甲还是乙?
解:∵V
V
又∵用电器两端电压在150~170V之间
∴该用电器是甲。
26.如图,15只空油桶(每只油桶底面的直径均为50cm)堆在一起,
要给它们盖一个遮雨棚,遮雨棚起码要多高?(结果精确到0.1cm)
解:如图设每只油桶底面的直径为dcm,
AB=hcm,则AC=4dcm,BC=2dcm,
这堆油桶的高度为h+d=
=
=2
=(2+1)d
=(2+1)
答:遮雨棚起码要223.2cm.
A
B
C
第二章 实数
复习回顾
兴宁市大坪中学 练小盛
1.熟练掌握算术平方根,平方根,立方根的相关概念.
2.熟练掌握无理数的概念,会对一个无理数进行估算.
3.掌握实数的定义,能熟练地进行实数的化简和计算.
学习目标:
本章主要内容
实数及相关概念
无理数的引入
无理数的表示
一、复习回顾
1、无理数的定义:
无限不循环小数叫做无理数
2、有理数的定义:
有限和无限循环小数叫做有理数
或整数与分数统称为有理数
3.算术平方根的定义及性质
定义:一个 正数x 的平方等于a,则 x 叫 a 的 算术平方根. 记作:X = (a≥0)
0的算术平方根是0.
因为 表示 a 的算术平方根,
所以 ≥0 (a≥0)
4.平方根的定义及性质
定义:一个数 x 的平方等于a,即x2=a,则 x 叫 a 的平方根. 记作: X= (a≥0)
0的平方根是0.
性质:
一个正数有两个平方根,它们互为相反数.
0的平方根是0.
负数没有平方根.
定义:一个数 x 的立方等于a,即x3=a,则 x 叫 a 的立方根. 记作: X=
0的立方根是0.
5.立方根的定义及性质
性质:
一个正数有一个正的立方根,
一个负数有一个负的立方根.
0的立方根是0.
6.实数的定义及实数的运算法则
定义:有理数和无理数统称实数.
分类:
(按定义分) (按大小分)
有理数 正实数
实数 实数 0
无理数 负实数
实数与数轴上的点一一对应,实数可以比较大小.
实数有相反数,倒数,绝对值.有理数的运算法则和运算律
在实数范围内仍然适用.
6、实数的分类
实数
数
数
整数
分数
正整数
负整数
负分数
正分数
正无理数
负无理数
有限小数或循环小数
无限不循环小数
有理
无理
7、实数的性质:
在实数范围内,相反数、倒数、
绝对值的意义和有理数的相反数、倒数、绝对值的意义完全一样。
例如:
是一个实数,它的相反数为 ;
绝对值为 .如果 那么它的
倒数为 .
1
7、实数的性质:
在实数范围内,相反数、倒数、
绝对值的意义和有理数的相反数、倒数、绝对值的意义完全一样。
>0)
反之
(a≥0,b>0)
8.无理数的乘除法则
算术平方根 平方根 立方根
表示方法
的取值
性
质
≥
开方
≥
正数
0
负数
正数(一个)
0
没有
互为相反数(两个)
0
没有
正数(一个)
0
负数(一个)
求一个数的平方根
的运算叫开平方
求一个数的立方根
的运算叫开立方
≠
是本身
0,1
0
0,1,-1
结合所学知识,完成下表:
9.每个实数都可以用数轴上的
一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上点是一一对应的.
同样,在数轴上,右边的点表示的数比左边的点表示的数大.
数轴上一个点
有一个实数
点 数
有一个实数
数轴上一个点
数 点
要点、考点聚焦
1.几个重要的运算律:
(1)加法的交换律:a+b=b+a
(2)加法的结合律:(a+b)+c=a+(b+c)
(3)乘法的交换律:ab=ba
(4)加法的结合律:(ab)c=a(bc)
(5)乘法对加法的分配律:a(b+c)=ab+ac
2.实数的运算主要有:加、减、乘、除、乘方、开方.实数的运算顺序:先乘方、开方,再乘、除,最后算加、减,有括号的先算括号里面的.
3.科学记数法的一般形式为:a×10n(1≤a≤10,n为整数).
4.有效数字是指一个数从左边第一个不为零的数字起到右边所有的数字.
复习题
1.把下列各数写入相应的集合中:,0.3,,,
0,0.5757757775(相邻两个5之间7的个数逐次加1).
(1)正数集合
(2)负数集合
(3)有理数集合
(4)无理数集合
,0.3, , , 0.5757757775
,
,0.3, ,
, , 0.5757757775
2.求下列各数的平方根和算术平方根。
(1)2.25;(2)361;(3);(4)
解:(1)∵
∴
即2.25的平方根是,算术平方根是1.5
(2)∵
∴
即361的平方根是,算术平方根是19
2.求下列各数的平方根和算术平方根。
(1)2.25;(2)361;(3);(4)
解:(3)∵
∴
即的平方根是,算术平方根是
(4)∵
∴
即的平方根是,算术平方根是
3.求下列各数的立方根:
(1)512;(2)0.008:;(3);(4)
解:(1)∵
∴
(2)∵
∴
(3)∵
∴
(4)∵
∴
4.求下列各式的值:
(1);(2);(3);
(4);(5);(6)
(1)解:原式
(2)解:原式
(3)解:原式
(4)解:原式
(5)解:原式
(6)解:原式
5.用计算器求下列各式的值(结果精确到0.01):
(1);(2);(3);
(4);(5)
解:(1)
(2)
(3)
(4)
(5)
6.估算下列各数的大小:
(1)(结果精确到0.1);(2)(结果精确到1)
解:(1)∵4
∴6.6
∴
(2)∵6
∴4
∴
7.比较下列各组数的大小:
(1),1;(2);(3)
解:(1)∵ =1.5,
∴ 1
(2)∵ , 1.414
∴
(3)∵ ,
∴
8.计算:
(1);(2);(3)()()
(4)2;(5);(6)
(1)解:原式=
=32
=1
(2)解:原式=
=5
(3)解:原式=
=32
=1
(4)解:原式=2
=4
=16
8.计算:
(1);(2);(3)()()
(4)2;(5);(6)
(5)解:原式=
=
(6)解:原式=4
=
9.求代数式
(1)
解:(1)把代入中,得
原式=
=
=4
解:(2)将代入中,得
原式=
=
=2
10.如图,已知OA=OB。
(1)说出数轴上点A所表示的数;
(2)比较点A所表示的数与-2.5的大小。
-3
-2
-1
0
1
1
A
B
解:(1)点A表示
(2)∵
又∵6.25
∴6.255
∴
11.如图,在长方形ABCD中,∠DAE=∠CBE=45
求面积和周长(结果精确到0.01)
A
B
C
D
E
解:∵长方形ABCD中,∠D=90,∠DAE=45,AD=1
∴∠AED=45,DE=AD=1
同理可得∠BEC=45,CE=1
∴∠AEB=180,AE=BE=
∴=1,AB=
∴2+2
12.在数轴上找出表示下列各数的点:
解:如图,点D就是所要表示的点。
0
1
2
3
4
1
B
A
C
D
12.在数轴上找出表示下列各数的点:
解:如图,点B就是所要表示的点。
0
1
2
3
4
2
B
A
12.在数轴上找出表示下列各数的点:
解:如图,点B就是所要表示的点。
0
1
2
3
4
B
A
13. 1,2,3,4,5,6,7,8,9,10,的平方根和立方根中,哪些是有理数?
哪些是无理数?
解:1,2,3,4,5,6,7,8,9,10的平方根分别是±1,±, ±,
±2,±, ±, ±3, ±.
1,2,3,4,5,6,7,8,9,10的立方根分别是1,, , ,
, 2, 。
有理数有±1, ±2, ±3,1,2
无理数有±, ±, ±, ±,±,
, , , , 。
14.填空题:
(1)一个数的平方等于它本身,这个数是 ;
(2)平方根等于本身的数是 ;
(3)算术平方根等于本身的数是 ;
(4)立方根等于本身的数是 ;
(5)大于0且小于的整数是 ;
(6)满足整数是 ;
0,1
0
0,1
0,±1
1,2,3
1,0,1,2
15.判断题:
(1)不带根号的数都是有理数; ( )
(2)两个无理数的和还是无理数。 ( )
?
?
16.“无理数就是开方开不尽的数”这句话对吗?请举例说明。
答:不对。如无理数等是无理数,但不是开方开不尽的数。
17.如图,每个小正方形的边长为1,剪一剪,并拼成一个正方形,
这个正方形的边长是多少?
答:边长是。
18.一个圆的半径为1cm,和它等面积的正方形的边长是多少厘米?
(结果精确到0.01cm)
解:设正方形的边长为cm,依题意,得
答:正方形的边长约为1.77厘米。
19.一个正方体形状的木箱容积是4,求此木箱的棱长(结果精确到0.1m).
解:设木箱的棱长为m,依题意,得
答:木箱的棱长约为1.6米。
20.一个篮球的体积为9850c,求该篮球的半径r
(3.14,结果精确到0.1cm).
解:
=
r
答:该篮球的半径约为13.3cm。
21.一个长方形的长与宽的比是5:3,它的对角线长为cm,求这个长方形的长与宽(结果精确到0.1cm).
解:设长方形的长为5cm,宽为3cm,依题意,得
解得x=
所以57.1cm,34.2cm
答:长方形的长约为7.1厘米,宽约为4.2厘米。
22.设一个三角形的三边依次为a,b,c,p=(a+b+c),则有下列面积公式:S=
S=(秦九韶公式)
(1)一个三角形的三边长依次为5,6,7,利用两个公式分别求这个三角形的面积.
(2)一个三角形的三边长依次为,利用两个公式分别求这个三角形的面积.
解:(1)∵P==9
∴海伦公式S==
秦九韶公式S==6
22.设一个三角形的三边依次为a,b,c,p=(a+b+c),则有下列面积公式:S= S=(秦九韶公式)
(1)一个三角形的三边长依次为5,6,7,利用两个公式分别求这个三角形的面积.
(2)一个三角形的三边长依次为,利用两个公式分别求这个三角形的面积.
解:(2)∵P=
∴S=
=
秦九韶公式S=
=
23.座钟的摆钟摆动一个来回所需的时间称为一个周期,其计算公式
T=2,其中T表示周期(单位:s),l表示摆长(单位:m),取3.14,
g=9.8m/.假如一台座钟的摆长伟0.5m,它每摆动一个来回发出一次滴
答声,那么在1min内,该座钟大约发出了多少次滴答声。
解:把,g=9.8m/,=0.5m代入T=2中,得
T=2 次
答:该座钟大约发出了42次滴答声。
24.交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度,所用的
经验公式是=16,其中v表示车速(单位:km/h),d表示刹车后车轮滑过
的距离(单位:m),f表示摩擦因数。在某次交通事故调查中,测得
d=20m,f=1.2,肇事汽车的车速大约是多少?(结果精确到0.1km/h)
解:把d=20m,f=1.2代入=16中,得
V16=16
答:肇事汽车的车速大约是78.4km/h
25.用电器的电阻R、功率P与它两端的电压U之间有关系:P=.有两个外观
完全相同的用电器,甲的电阻伟18.4Ω,乙的电阻伟20.8Ω。现测得某电器
的功率为1500W,两端电压在150~170V,该用电器到底是甲还是乙?
解:∵V
V
又∵用电器两端电压在150~170V之间
∴该用电器是甲。
26.如图,15只空油桶(每只油桶底面的直径均为50cm)堆在一起,
要给它们盖一个遮雨棚,遮雨棚起码要多高?(结果精确到0.1cm)
解:如图设每只油桶底面的直径为dcm,
AB=hcm,则AC=4dcm,BC=2dcm,
这堆油桶的高度为h+d=
=
=2
=(2+1)d
=(2+1)
答:遮雨棚起码要223.2cm.
A
B
C
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
