14.7 等边三角形 课件(16张PPT)
文档属性
| 名称 | 14.7 等边三角形 课件(16张PPT) | 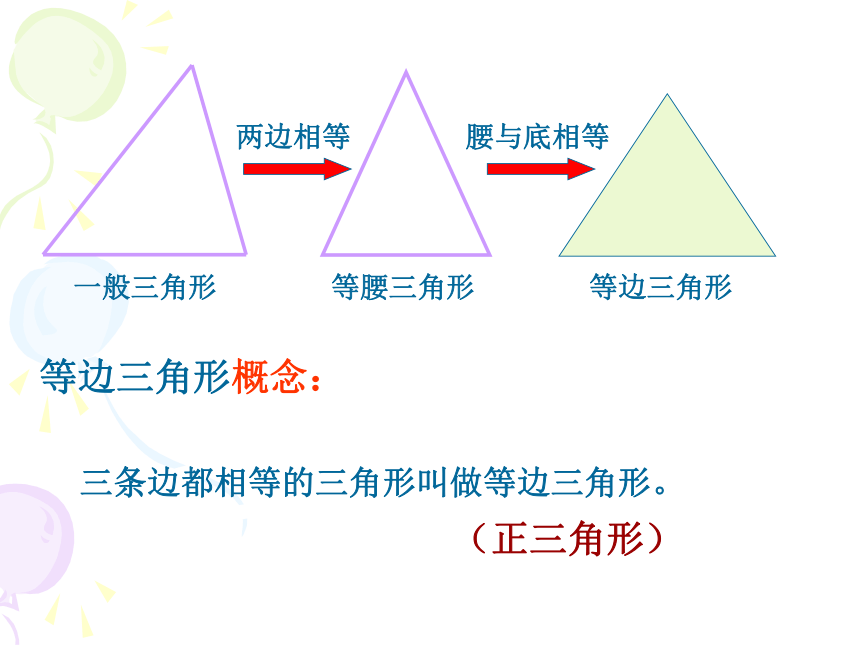 | |
| 格式 | zip | ||
| 文件大小 | 286.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-01-10 15:12:47 | ||
图片预览






文档简介
(共16张PPT)
等腰三角形
等边三角形
一般三角形
三条边都相等的三角形叫做等边三角形。
两边相等
腰与底相等
等边三角形概念:
(正三角形)
已知:
AB=AC=BC,
求证:∠A=
∠B=
∠C
证明
∵AB=AC
∴∠B=∠C
(等边对等角)
同理
∠A=∠C
∴∠A=∠B=∠C
∵
∠A+∠B+∠C=180°
(三角形的内角和为180°
)
∴
∠A=
∠B=
∠C=60
°(等式性质)
结论:
等边三角形的三个内角都相等,并且
每个内角都等于60
°.
A
B
C
等边三角形中也有三线合一吗
结论:
等边三角形各边上中线,高和所对角
的平分线都三线合一,它们交于一点,
这点叫三角形的中心.
A
B
C
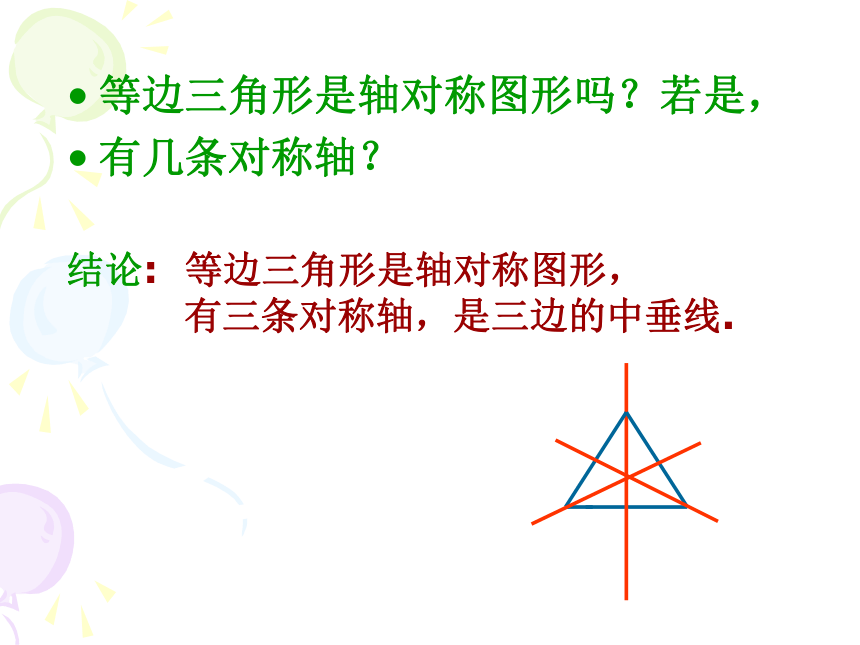
等边三角形是轴对称图形吗?若是,
有几条对称轴?
结论:
等边三角形是轴对称图形,
有三条对称轴,是三边的中垂线.
等边三角形的性质
1.等边三角形的三边相等。
2.等边三角形的内角都相等,且等于60
°
4.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的
平分线都三线合一.
类比等腰三角形的判定研究等边三角形有哪些判定方法
小提示
可以从边与角两类元素加以考虑;也可以从性质的“逆”加以考虑。
已知:
∠A=∠B=∠C
求证:
AB=AC=BC
证明:∵∠A=∠B
∴
AC=BC
(等角对等边)
∵
∠B=∠C
∴
AB=AC(等角对等边)
∴
AB=AC=BC
∴△ABC是等边三角形.
(三边相等的三角形是等边三角形)
A
B
C
已知:AB=AC
(1)若∠A=60
°求证:
△ABC是等边三角形
(2)若∠
B=60
°求证:
△ABC是等边三角形
证明:
(1)
∵
AB=AC.
∴
∠
B=
∠
C
(等边对等角)
∵
∠A+∠B+∠C=180°
(三角形的内角和为180°
)
且∠A=60
°
∴
∠
B=
∠
C=
60
°
(等式性质)
∴
∠A=
∠
B=
∠
C
∴
△ABC是等边三角形.
(三个内角相等的三角形是等边三角形)
(2)
∵
AB=AC.
∴
∠
B=
∠
C
(等边对等角)
∵
∠
B=60
°
∴
∠C=
60
°
∵
∠A+∠B+∠C=180°
(三角形的内角和为180°
)
∴
∠A
=
60
°
(等式性质)
∴
∠A=
∠
B=
∠
C
∴
△ABC是等边三角形.
(三个内角相等的三角形是等边三角形)
A
B
C
等边三角形
一般三角形
三边相等
边的条件
等边三角形
一般三角形
三角相等
角的条件
等腰三角形
等边三角形
一般三角形
两边相等
一个角60
°
等边三角形的判定方法:
1.三边相等的三角形是等边三角形.
三边
2.三个内角都相等的三角形是等边三
角形.
三角
3.有一个内角等于60
°的等腰三角
形是等边三角形.
等腰+
60
°
2、已知△ABC中,∠A=∠B=60°,AB=3cm
则△ABC的周长________
3、
△ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______
1、等边三角形是_______对称图形,它有_______条对称轴,是_________________。
小试牛刀
4、已知△ABC中,AB=AC,
∠A+∠B=120°,那么∠A=______;△ABC是______三角形;
如图,
△ABC中,D、E是BC边上的三等分点,
△AED是等边三角形,则∠BAC为( )度?
看谁反应快
例1:如图,△ABC和△CDE都是等边三角形,试说明BE=AD的理由
A
B
C
D
E
一、等边三角形的性质.
二、
等边三角形的判定:
1.三边相等的三角形是等边三角形.
2.三个内角都相等的三角形是等边三角形.
3.有一个内角等于60
°的等腰三角形是等边
三角形.
1.等边三角形的三边相等。
2.等边三角形的内角都相等,且等于60
°
4.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的
平分线都三线合一.
布置作业14.7
谢谢
等腰三角形
等边三角形
一般三角形
三条边都相等的三角形叫做等边三角形。
两边相等
腰与底相等
等边三角形概念:
(正三角形)
已知:
AB=AC=BC,
求证:∠A=
∠B=
∠C
证明
∵AB=AC
∴∠B=∠C
(等边对等角)
同理
∠A=∠C
∴∠A=∠B=∠C
∵
∠A+∠B+∠C=180°
(三角形的内角和为180°
)
∴
∠A=
∠B=
∠C=60
°(等式性质)
结论:
等边三角形的三个内角都相等,并且
每个内角都等于60
°.
A
B
C
等边三角形中也有三线合一吗
结论:
等边三角形各边上中线,高和所对角
的平分线都三线合一,它们交于一点,
这点叫三角形的中心.
A
B
C
等边三角形是轴对称图形吗?若是,
有几条对称轴?
结论:
等边三角形是轴对称图形,
有三条对称轴,是三边的中垂线.
等边三角形的性质
1.等边三角形的三边相等。
2.等边三角形的内角都相等,且等于60
°
4.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的
平分线都三线合一.
类比等腰三角形的判定研究等边三角形有哪些判定方法
小提示
可以从边与角两类元素加以考虑;也可以从性质的“逆”加以考虑。
已知:
∠A=∠B=∠C
求证:
AB=AC=BC
证明:∵∠A=∠B
∴
AC=BC
(等角对等边)
∵
∠B=∠C
∴
AB=AC(等角对等边)
∴
AB=AC=BC
∴△ABC是等边三角形.
(三边相等的三角形是等边三角形)
A
B
C
已知:AB=AC
(1)若∠A=60
°求证:
△ABC是等边三角形
(2)若∠
B=60
°求证:
△ABC是等边三角形
证明:
(1)
∵
AB=AC.
∴
∠
B=
∠
C
(等边对等角)
∵
∠A+∠B+∠C=180°
(三角形的内角和为180°
)
且∠A=60
°
∴
∠
B=
∠
C=
60
°
(等式性质)
∴
∠A=
∠
B=
∠
C
∴
△ABC是等边三角形.
(三个内角相等的三角形是等边三角形)
(2)
∵
AB=AC.
∴
∠
B=
∠
C
(等边对等角)
∵
∠
B=60
°
∴
∠C=
60
°
∵
∠A+∠B+∠C=180°
(三角形的内角和为180°
)
∴
∠A
=
60
°
(等式性质)
∴
∠A=
∠
B=
∠
C
∴
△ABC是等边三角形.
(三个内角相等的三角形是等边三角形)
A
B
C
等边三角形
一般三角形
三边相等
边的条件
等边三角形
一般三角形
三角相等
角的条件
等腰三角形
等边三角形
一般三角形
两边相等
一个角60
°
等边三角形的判定方法:
1.三边相等的三角形是等边三角形.
三边
2.三个内角都相等的三角形是等边三
角形.
三角
3.有一个内角等于60
°的等腰三角
形是等边三角形.
等腰+
60
°
2、已知△ABC中,∠A=∠B=60°,AB=3cm
则△ABC的周长________
3、
△ABC是等腰三角形,周长为15cm且∠A=60°,则BC=_______
1、等边三角形是_______对称图形,它有_______条对称轴,是_________________。
小试牛刀
4、已知△ABC中,AB=AC,
∠A+∠B=120°,那么∠A=______;△ABC是______三角形;
如图,
△ABC中,D、E是BC边上的三等分点,
△AED是等边三角形,则∠BAC为( )度?
看谁反应快
例1:如图,△ABC和△CDE都是等边三角形,试说明BE=AD的理由
A
B
C
D
E
一、等边三角形的性质.
二、
等边三角形的判定:
1.三边相等的三角形是等边三角形.
2.三个内角都相等的三角形是等边三角形.
3.有一个内角等于60
°的等腰三角形是等边
三角形.
1.等边三角形的三边相等。
2.等边三角形的内角都相等,且等于60
°
4.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的
平分线都三线合一.
布置作业14.7
谢谢
